統計学で最も一般的な検定方法はt検定であり、2群間の差を比較することができます。ただデータの中には、3群以上が含まれていることがあります。この場合、2群の差を比較する検定法を利用するのではなく、3群以上の差を検定できる方法を利用しましょう。
3群以上のデータをもつ標本について、差があるかどうかを比較する方法が分散分析(ANOVA)です。分散分析には複数の種類があり、それぞれの方法について使い方を理解しなければいけません。
また分散分析によって差があるとわかった場合、それぞれの群について2群検定をします。ただ誤差が大きくなるため、ボンフェローニ補正を利用することによって多重比較をします。
2群をもつ標本に比べて、3群以上の標本では事前に理解するべきポイントがあります。そこで、どのように分散分析を利用し、3群以上の差を検定すればいいのか解説していきます。
もくじ
3つ以上のグループを比較する方法が分散分析
分散分析(ANOVA)では、3つ以上のグループを比較することができます。統計学の検定手法で最初に学ぶt検定というのは、2つのデータに差があるかどうかを比較する方法であり、3つ以上のグループを比較することはできません。
そのため、以下のように使い分けましょう。
- 2群の比較:t検定
- 3群以上の比較:分散分析
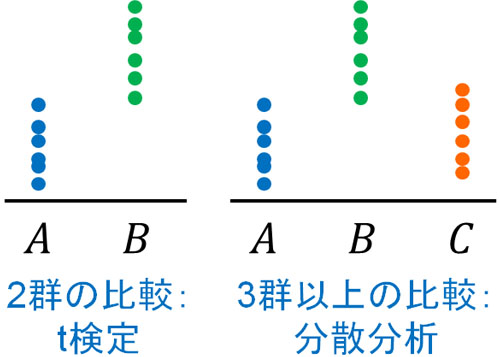
t検定と分散分析には、このような違いがあります。
どのグループ間に有意差があるのかを判断することはできない
なお分散分析によって有意差があると判断できるとき、どのように考えればいいのでしょうか。例えばA群、B群、C群がある場合、帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:A群、B群、C群で差はない
- 対立仮説:A群、B群、C群のどれかに差がある
有意差がなく帰無仮説が採用される場合、すべての母平均で差がないと判断できます。「母平均が同じ」と述べることはできないものの、差がないことはわかります。
一方で有意差がある場合、どのように考えればいいのでしょうか。分散分析で重要なのは、グループ間に差があることはわかるものの、どの群で差があるのかわからないことです。つまり、以下のケースではどれも「有意差がある」と判定されます。
- AとBに差がある(AとCは差がない)
- AとCに差がある(AとBは差がない)
- AとCに差がある(BとCは差がない)
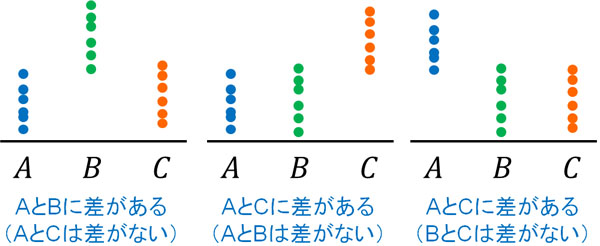
分散分析でP値を確認し、有意差があるとわかっても、どのグループ間で差があるのか判断することはできません。そのため分散分析をしたあと、さらに解析を進める必要があります。
分散分析には複数の種類がある
このとき、分散分析には複数の種類があります。そこで、どのような方法を利用すればいいのか理解しましょう。分散分析で重要なのは主に以下の4つです。
- 一元配置分散分析
- クラスカル・ウォリス検定
- 二元配置分散分析
- フリードマン検定
どれも異なる検定法であり、利用場面は違います。ただ見分け方は簡単であり、以下のように使い分けましょう。
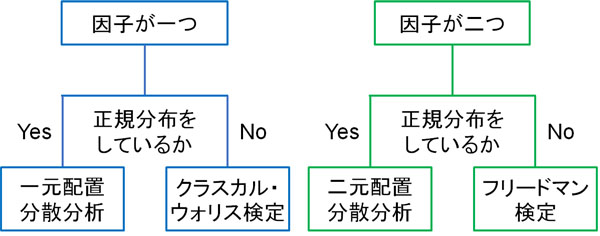
このように、標本によって利用する検定法を使い分けましょう。
因子が一つの場合では、一元配置分散分析またはクラスカル・ウォリス検定が利用されます。母集団が正規分布する場合、パラメトリック検定である一元配置分散分析を利用します。一方で母集団が正規分布するかどうか不明な場合、ノンパラメトリック検定であるクラスカル・ウォリス検定を利用しましょう。
また標本には、因子が二つのケースもあります。この場合は二元配置分散分析またはフリードマン検定を利用します。
二元配置分散分析はパラメトリック検定であり、母集団が正規分布する場合に利用できます。一方で母集団が正規分布するかどうか不明なとき、ノンパラメトリック検定であるフリードマン検定が有効です。
なお2群検定での「対応のあるt検定」や「対応のないt検定」などで分類すると以下のようになります。
- 対応のないt検定に相当(パラメトリック検定):一元配置分散分析
- マン・ホイットニーのU検定に相当(ノンパラメトリック検定:対応なし):クラスカル・ウォリス検定
- 対応のあるt検定に相当(パラメトリック検定):二元配置分散分析
- ウィルコクソンの符号順位検定に相当(ノンパラメトリック検定:対応あり):フリードマン検定
標本によって利用する検定法は異なるものの、こうした分散分析の中から最適な方法を選ぶようにしましょう。
2群検定を利用し、どの群の間に差があるのか確認する
なお前述の通り、分散分析をしたとしても「どのグループの間で差があるのか」を知ることはできません。そのため、以下の順番によって解析します。
- 分散分析を行う
- 差があるとわかった場合、2群検定による多重比較を行う
- 多重比較をするとき、ボンフェローニ法を利用する
分散分析によって有意差があるとわかった場合、それぞれの群について2群検定をしましょう。2標本t検定などを利用することによって、どの群の間に差があるのかそれぞれ調べるのです。例えばA群、B群、C群がある場合、2群検定によって以下をそれぞれ調べます。
- A群とB群
- A群とC群
- B群とC群
このようにそれぞれを検定すれば、どのグループ間で差があるのか明確にわかります。分散分析では差がある群を判断できないため、何回も2群検定を行うというわけです。
検定の多重性の問題を解決するため、多重比較法を行う
ただ、何度も2群検定を行うと不都合なことが起こります。本来であれば差がないにも関わらず、差があると判断されることが頻繁に発生するのです。これを検定の多重性の問題といいます。
なぜ、検定の多重性の問題が発生するのでしょうか。統計処理をするとき、通常は母集団の平均値について真の値がわからない状態で検定をします。このとき95%信頼区間というのは、「標本データを集めて100回測定すると、95%の確率で真の値を含む」ことを意味します。
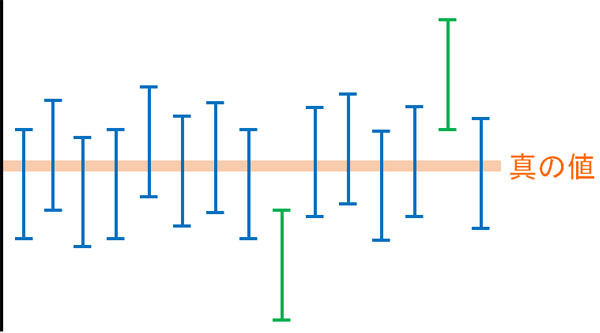
つまり、真の値から外れるケースもあるのです。そのため何度も検定をすると、「本来は差がないにも関わらず、たまたま有意差が出てしまうケース」を含む可能性が高くなります。
例えばA群、B群、C群で2群検定をする場合、3回の2群検定をすることになります。この場合、それぞれの有意水準と0.05します。このとき検定を3回行う場合、すべてで正しい答えを得られる確率は0.86(86%)です。
\(0.95×0.95×0.95≒0.86\)
つまり、14%の確率で「本来は差がないにも関わらず、差があると判定されてしまう」ことになります。「クジで当たる確率が5%だとしても、3回引けば14%の確率で少なくとも一回は当たる」という理屈と同じわけです。何度もクジを引けば当たりを得られる確率は上昇するのです。
統計処理をするとき、有意水準は0.05(5%)や0.01(1%)を利用します。それにも関わらず、全体の有意水準が0.14(14%)になってはいけません。そのため多重比較法を利用します。
ボンフェローニ法による多重比較を行う
多重比較法ではP値を補正します。P値が0.05であったとしても、3回の2群検定をすると前述の通りP値が0.14になってしまうからです。また、検定回数が多くなるとP値はより大きくなります。P値の補正が必要なのはこうした理由があるからです。
多重比較法にはテューキー法やダネット法、スティール・ドゥワス法などがあります。ただこれら多重比較法の中でも、最も一般的で頻繁に利用される方法がボンフェローニ法です。そこで、ボンフェローニ補正のやり方を学びましょう。
ボンフェローニ法は非常に簡単であり、すぐに理解することができます。具体的には、2群検定で得た確率(P値)に対して、検定回数をかけ算しましょう。
例えばA群、B群、C群でそれぞれ2群検定を行い、以下の結果を得られたとします。
- A群とB群:\(P=0.02\)
- A群とC群:\(P=0.08\)
- B群とC群:\(P=0.01\)
この場合、「A群とB群」「B群とC群」で有意差があると判断できます。ただ前述の通り、検定の多重性の問題を考慮しなければいけません。そこでボンフェローニ法を利用し、検定回数をP値にかけましょう。
今回の場合、3回の2群検定をしています。そこで、それぞれのP値に3をかけましょう。
- A群とB群:\(P=0.02×3\)\(=0.06\)
- A群とC群:\(P=0.08×3\)\(=0.24\)
- B群とC群:\(P=0.01×3\)\(=0.03\)
ボンフェローニ補正をした結果、有意差があるのは「B群とC群」のみであるとわかります。多重比較法を利用することによって検定の多重性の問題を回避し、差のあるグループを判断できるのです。
・ボンフェローニ法ではP値の基準を下げても問題ない
なおボンフェローニ法を利用するとき、検定回数によってP値の基準を下げても問題ありません。有意水準に対して、検定回数で割ることで新たな有意水準を得るのです。
例えば有意水準を0.05とする場合、2群検定を3回するのであれば、新たな有意水準として0.0167を設定します。
\(\displaystyle\frac{0.05}{3}≒0.0167\)
先ほど説明した方法とまったく同じことをしていますが、このやり方によって有意差を判断しても問題ありません。この場合、2群検定の回数によって以下のようにP値を下げましょう。
| 検定回数 | 有意水準 |
| 1回 | 0.05 |
| 2回 | 0.025 |
| 3回 | 0.0167 |
| 4回 | 0.0125 |
有意水準0.05に対してボンフェローニ補正をしたい場合、検定回数がN回なのであれば、\(\displaystyle\frac{0.05}{N}\)によって新たな有意水準を得ることができます。
ボンフェローニ法を利用する多重比較法は簡単であり、理解しやすいです。このようにしてP値を補正し、グループ間に差があるかどうかを確認しましょう。
分散分析と多重比較法を利用し、多群間での差を確認する
2群で差があるかどうか確認できるようになった後、次は多群の検定を学ぶことになります。そこで重要なのが分散分析(ANOVA)です。
分散分析には種類があります。一元配置分散分析、クラスカル・ウォリス検定、二元配置分散分析、フリードマン検定について、どのような違いがあるのか理解しましょう。
また有意差があるとわかった場合、2群検定を利用して、どのグループ間で差があるのか確認します。ただ検定の多重性の問題を解決する必要があります。そこで多重比較法を利用する必要があり、特に活用されるのがボンフェローニ法です。ボンフェローニ補正を行い、グループ間の差を確認しましょう。
3群以上をもつ標本では、検定の方法が少し複雑になります。そこで分散分析や多重比較法を用いて、それぞれの群の間に差があるかどうか検定できるようになりましょう。






