統計学で最も重要な分布が正規分布です。ただ統計では多くの分布の種類があり、その一つが幾何分布です。幾何分布は正規分布のように重要な分野ではないものの、統計を学ぶときに幾何分布を勉強しなければいけないケースは多いです。
高校数学で確率や等比数列を理解している場合、幾何分布が何を意味しているのかわかります。概念は難しくないものの、期待値や分散の計算をするためには確率を理解しなければいけません。
また、幾何分布には無記憶性という性質があります。離散型確率分布の中でも、幾何分布に特有の性質が無記憶性です。そこで、無記憶性が何を意味しているのか理解しましょう。
高校数学の知識があれば幾何分布を理解できます。そこで幾何分布の性質や期待値・分散の出し方、無記憶性の特徴を解説していきます。
もくじ
幾何分布ではベルヌーイ試行を利用して定める
幾何分布を学ぶ前にベルヌーイ試行を理解しなければいけません。ベルヌーイ試行とは、「二者択一(結果が2つのみ)であり、独立な試行」を指します。
例えばコインを投げるとき、結果は表と裏のみです。また、確率はそれぞれ\(\displaystyle\frac{1}{2}\)です。そのためコイン投げというのは、確率が一定のベルヌーイ試行です。
またサイコロについてもベルヌーイ試行です。出る目が1の場合を成功、それ以外の目が出たら失敗とすると、結果は2つのみです。また成功確率は\(\displaystyle\frac{1}{6}\)であり、失敗確率は\(\displaystyle\frac{5}{6}\)です。これが、サイコロを投げるときにベルヌーイ試行となる理由です。
幾何分布ではベルヌーイ試行を利用します。また幾何分布というのは、「初めて成功する確率はいくらか」を表します。例えば「サイコロを投げ、1の目が出ると成功と判定する」とします。
それではサイコロを5回投げ、ようやく1の目が出る場合、確率はいくらでしょうか。5回目に成功となるため、4回目までは連続して1以外の目が出ることになります。そのため、4回目まで失敗する確率(1の目以外が出る確率)は\(\left(\displaystyle\frac{5}{6}\right)^4\)です。
4回目まで失敗した後、5回目に1の目が出るため、以下の式によって確率を計算できます。
\(\left(\displaystyle\frac{5}{6}\right)^4×\displaystyle\frac{1}{6}\)
このように幾何分布では、失敗確率と失敗回数を利用して式を作った後、成功確率をかけます。
次に、これを数式で表しましょう。成功確率をpとすると、失敗確率は\(1-p\)です。また成功するまでの試行回数を\(k\)とすると、連続して失敗する回数は\(k-1\)です。そのため、幾何分布での確率\(P(X=k)\)は以下になります。
- \(P(X=k)=(1-p)^{k-1}×p\)
幾何分布の確率が「\(k\)回目に成功する確率」であることを理解すれば、なぜこの公式によって計算できるのかわかります。
幾何分布のグラフの形を理解する
それでは、幾何分布のグラフはどのような形になるのでしょうか。実際にグラフを作ってみましょう。
コインを投げる場合、表と裏の確率はそれぞれ\(\displaystyle\frac{1}{2}\)です。コインを投げて表が出るときを成功とすると、幾何分布(初めて表が出る確率)は以下のようになります。
- 1回目:\(\displaystyle\frac{1}{2}\)
- 2回目:\(\displaystyle\frac{1}{2}×\displaystyle\frac{1}{2}=\displaystyle\frac{1}{4}\)
- 3回目:\(\left(\displaystyle\frac{1}{2}\right)^2×\displaystyle\frac{1}{2}=\displaystyle\frac{1}{8}\)
- 4回目:\(\left(\displaystyle\frac{1}{2}\right)^3×\displaystyle\frac{1}{2}=\displaystyle\frac{1}{16}\)
- 5回目:\(\left(\displaystyle\frac{1}{2}\right)^4×\displaystyle\frac{1}{2}=\displaystyle\frac{1}{32}\)
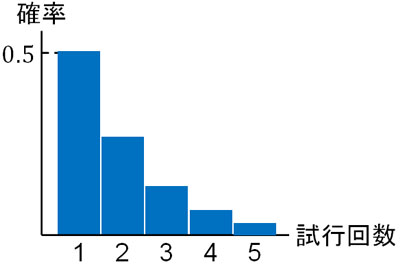
このように、幾何分布では試行回数\(k\)が多くなるに従って確率が減少していきます。すべての幾何分布について、このようなグラフの形となります。
当然ながら、試行回数が多いほど連続して失敗する確率は低くなります。そのため試行回数が多くなると、幾何分布の確率が減少するのは理解できると思います。
連続して失敗する確率を幾何分布と呼ぶケースもある
なお、幾何分布には2つの定義があります。そのため教科書や人によって説明が異なり、混乱する人がいるかもしれません。ただ定義が2つあるため、両方とも正解です。
ここまでの説明では、「\(k\)回目に成功するときの確率」を幾何分布と解説してきました。一方、幾何分布には「初めて成功する前に、連続して失敗する確率」という定義もあります。
この場合、公式は以下のようになります。
- \(P(X=k)=(1-p)^k×p\)
先ほどの公式に比べて、\(k\)の値が1つ少なくなります。また\((k=0,1,2…)\)となり、\(k\)の値は0からスタートします。こうした性質があるため、「\(k\)回目に成功するときの確率」を定義にする場合に比べて混乱しやすいです。
いずれにしても教科書によっては、「初めて成功する前に、連続して失敗する確率」が定義となっているケースがあることを理解しましょう。
幾何分布の確率関数の和(累積分布関数)は等比数列となる
次に、幾何分布の確率関数の和を求めてみましょう。確率をすべて足すとき、累積分布関数\(F(x)\)を利用します。累積分布関数とは、要は「すべての確率を足すこと」を指します。
そこで先ほど解説した以下の公式について、すべて足す場合を考えてみましょう。
- \(P(X=k)=(1-p)^{k-1}×p\)
すべての確率を足す場合、以下の計算式になります。
\(p+p(1-p)+p(1-p)^2\)\(+…\)\(+p(1-p)^{n-1}\)
\(=\displaystyle\sum_{k=1}^{n}{p(1-p)^{k-1}}\)
これはつまり、初項p、公比\((1-p)\)の等比数列であることがわかります。等比数列をすべて足す場合、以下の公式になります。
\(\displaystyle\sum_{k=1}^{n}{ar^{k-1}}=\displaystyle\frac{a(1-r^n)}{1-r}\)
※\(a\)は初項、\(r\)は公比
等比数列の和の公式を利用すると、幾何分布での累積分布関数\(F(x)\)を導き出すことができます。また、すべての確率を足す場合の計算式は以下です。
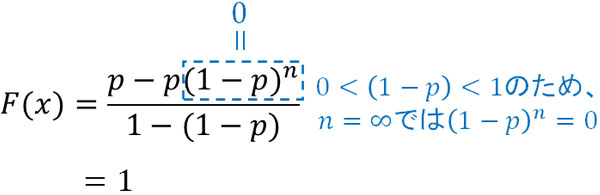
当然ではありますが、すべての確率を足すと1(100%)になります。ここまでの解説で重要なのは、幾何分布の確率を足すときは等比数列になることです。
確率Pの幾何分布について、期待値(平均)を計算する
それでは、幾何分布の期待値\(E(X)\)はどのように計算すればいいのでしょうか。幾何分布で期待値(平均)を得る公式は以下になります。
- \(E(X)=\displaystyle\frac{1}{p}\)
この公式を導き出しましょう。まず、期待値\(E(X)\)はそれぞれの確率変数と期待値をかけた後、すべて足すことによって得られます。
- 期待値\(=X_1P_1+X_2P_2+…+X_nP_n\)
- 期待値\(=\displaystyle \sum_{k=1}^n X_kP_k\)
幾何分布では確率変数\(k\)、確率Pは\(p(1-p)^{k-1}\)です。そこで、無限大(∞)まで足すときの期待値を計算しましょう。以下のようになります。
\(E(X)=p(1-p)^0\)\(+2p(1-p)^1\)\(+3p(1-p)^2\)\(…\)
\(=\displaystyle \sum_{k=1}^∞ kp(1-p)^{k-1}\)
\(=p\displaystyle \sum_{k=1}^∞ k(1-p)^{k-1}\)
ここで、\(m=\displaystyle \sum_{k=1}^∞ k(1-p)^{k-1}\)としましょう。つまり、\(E(X)=pm\)です。また、\(m\)の両辺に\((1-p)\)をかけた後、\(m\)から引きましょう。
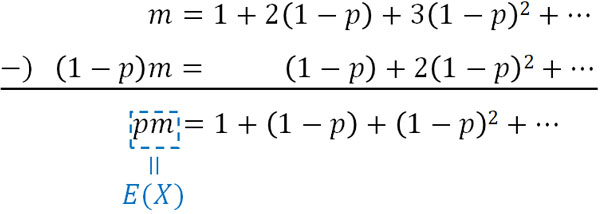
こうして、\(E(X)=pm\)は初項1、公比\((1-p)\)の等比数列であるとわかります。そのため等比数列の和の公式を利用し、以下のように期待値(平均)の公式を求めることができます。
\(E(X)=\displaystyle\frac{1}{1-(1-p)}\)
\(E(X)=\displaystyle\frac{1}{p}\)
なお確率\((1-p)\)は1よりも小さい値です。また\(k=n=∞\)(無限大)であり、\(n\)の値を極限まで大きくしていくと、先ほどの図で解説した通り\((1-p)^n=0\)になります。
こうして、幾何分布での期待値\(E(X)\)の公式を得ることができました。
幾何分布の分散(標準偏差)の出し方
次に分散(標準偏差)を得る公式を出しましょう。幾何分布での分散\(V(X)\)は以下の公式によって得ることができます。
\(V(X)=\displaystyle\frac{1-p}{p^2}\)
まず、分散\(V(X)\)は以下の公式によって得ることができると多くの人が既に学んでいると思います。
- \(V(X)=E(X^2)-E(X)^2\)
期待値の定義を利用して「幾何分布での期待値を出す公式」を得たのと同じように、分散の定義を利用して幾何分布での分散を出す公式を得ましょう。
・\(E(X^2)\)の計算
まず、\(E(X^2)\)を計算しましょう。\(E(X)\)\(=\displaystyle \sum_{k=1}^∞ kp(1-p)^{k-1}\)であるため、\(E(X^2)\)は以下のようになります。
\(E(X^2)=\displaystyle \sum_{k=1}^∞ k^2p(1-p)^{k-1}\)
\(=p\displaystyle \sum_{k=1}^∞ k^2(1-p)^{k-1}\)
次に、\(s=\displaystyle \sum_{k=1}^∞ k^2(1-p)^{k-1}\)としましょう。つまり、\(E(X^2)=ps\)です。また\((1-p)\)を両辺にかけ、\(s\)から引くと以下のようになります。
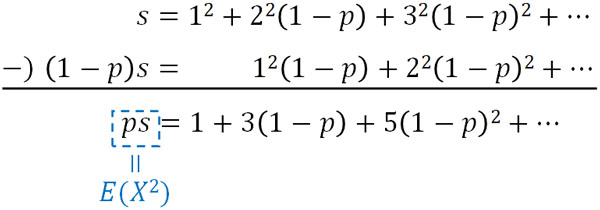
このように式を変形すると、\(E(X^2)\)は等差数列\((2k-1)\)と等比数列\((1-p)^{k-1}\)のかけ算であるとわかります。そこで、以下のように計算しましょう。
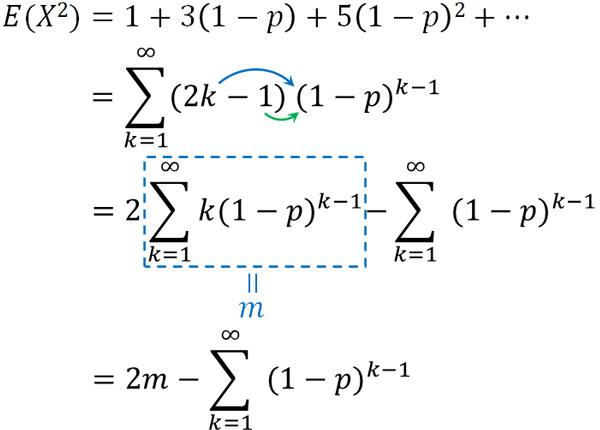
なお期待値の公式を得るとき、\(E(X)\)\(=mp\)\(=\displaystyle\frac{1}{p}\)であることを解説しました。つまり、\(m=\displaystyle\frac{1}{p^2}\)です。そのため、\(2m\)は\(\displaystyle\frac{2}{p^2}\)になります。
また式の右側について、初項1、公比\((1-p)\)の無限等比級数です。そのため、和は以下のようになります。
\(\displaystyle\sum_{k=1}^{∞}{(1-p)^{k-1}}\)
\(=\displaystyle\frac{1}{1-(1-p)}\)
\(=\displaystyle\frac{1}{p}\)
こうして\(E(X^2)\)は以下になるとわかります。
\(E(X^2)=\displaystyle\frac{2}{p^2}-\displaystyle\frac{1}{p}\)\(=\displaystyle\frac{2-p}{p^2}\)
なお期待値は\(E(X)=\displaystyle\frac{1}{p}\)とわかっているため、\(E(X)^2=\displaystyle\frac{1}{p^2}\)です。そのため、以下のようになります。
\(V(X)=E(X^2)-E(X)^2\)
\(=\displaystyle\frac{2-p}{p^2}-\displaystyle\frac{1}{p^2}\)
\(=\displaystyle\frac{1-p}{p^2}\)
こうして、幾何分布での分散の公式を得ることができました。なお幾何分布の標準偏差を得たい場合、平方根を利用して標準偏差を出しましょう。
幾何分布の無記憶性とは何か
それでは、幾何分布に特有の特徴を理解しましょう。幾何分布には無記憶性があります。無記憶性とは何なのでしょうか。
無記憶性とは、過去のイベントが将来に影響を与えないことを意味しています。幾何分布では、独立の試行だからです。ただ、これについては感覚的に理解できると思います。
例えばほかの人がコインを投げ、5回連続で裏(失敗)でした。その後、あなたがコインを投げて表(成功)になる確率はいくらでしょうか。当然、あなたが表を得る確率は\(\displaystyle\frac{1}{2}\)であり、裏になる確率は\(\displaystyle\frac{1}{2}\)です。
過去にたくさん失敗したとしても、将来の成功確率に影響を与えることはありません。例えば宝くじで何度外れたとしても、将来当たりクジを引く確率が高くなることはないのです。試行が独立の場合、幾何分布は無記憶性をもつのです。
無記憶性の証明と離散型確率分布との関係
それでは、幾何分布の無記憶性を証明してみましょう。\(m\)と\(n\)を正の整数とすると、無記憶性は以下の式で表されます。
\(P(X=m+n|X≥m)\)\(=P(X=n)\)
恐らく、この数式をみても意味を理解できないと思います。例えば、あなたがコイン投げをして\(n\)回目に成功したとします。\(P(X=n)\)というのは、あなたがコインを投げて\(n\)回目に初めて成功する確率を表しています。
ただ、あなたがコインを投げる前、ほかの人がコインを\(m\)回投げ、すべて失敗していたとします。この場合、\(P(X=m+n)\)は\(m+n\)回目に初めて成功する確率を意味しています。また、\(m\)回目以上の失敗を意味するのが\(X≥n\)です。
また\(P(X=m+n|X≥n)\)は条件付き確率であり、「\(m\)回目以上の失敗を連続でするとき(\(X≥m\)のとき)、\(m+n\)回目に成功する確率\(P(X=m+n)\)」を表しています。

\(n\)回目に成功する確率が\(m+n\)回目に成功する確率と等しい場合、それまでの\(m\)回の連続失敗は確率に影響しないことになります。数式で表すと理解は難しいですが、この式にはこのような意味があります。
なお条件付き確率を学ぶとき、以下の公式を既に習っていると思います。
\(P(A|B)=\displaystyle\frac{A∩B}{B}\)
そこで、この公式を利用して無記憶性の証明をしましょう。以下のようになります。
\(P(X=m+n|X≥m)\)\(=\displaystyle\frac{P((X=m+n)∩(X≥m))}{P(X≥m)}\)
なおm回以上連続で失敗し、かつ\(m+n\)回目で成功する確率というのは、要は\(m+n\)回目で初めて成功する確率を指します。つまり、\(P((X=m+n)∩(X≥m))\)\(=P(X=m+n)\)です。そのため、以下のようになります。
\(\displaystyle\frac{P((X=m+n)∩(X≥m))}{P(X≥m)}\)
\(=\displaystyle\frac{P(X=m+n)}{P(X≥m)}\)
なお幾何分布で確率を得る公式は\(P(X=k)\)\(=p(1-p)^{k-1}\)であるため、\(P(X=m+n)\)の確率は以下になります。
\(P(X=m+n)=p(1-p)^{m+n-1}\)
こうして、分子を得ることができました。次に分母を計算しましょう。
ここでは\(m\)回連続で失敗し、\(m+1\)回目に成功する場面を想定します。このときの確率は\(P(X=m)\)\(=p(1-p)^m\)です。また\(P(X≥m)\)とは、失敗が\(m\)回以上、連続して起こる確率です。失敗が\(m\)回以上連続するため、以下の確率を足していきます。
- 失敗が\(m\)回:\(P(X=m)\)
- 失敗が\(m+1\)回:\(P(X=m+1)\)
- 失敗が\(m+2\)回:\(P(X=m+2)\)
- ….
これを何度も足しましょう。すると、以下のような計算になります。

こうして、\(P(X≥m)=(1-p)^m\)であるとわかりました。そこで、\(\displaystyle\frac{P(X=m+n)}{P(X≥m)}\)へ代入しましょう。
\(\displaystyle\frac{P(X=m+n)}{P(X≥m)}\)
\(=\displaystyle\frac{p(1-p)^{m+n-1}}{(1-p)^m}\)
\(=p(1-p)^{n-1}\)
\(=P(X=n)\)(証明完了)
最初に解説した通り、幾何分布の公式は\(P(X=k)\)\(=p(1-p)^{k-1}\)です。そのため、\(n\)回目に初めて成功する確率は\(P(X=n)\)\(=p(1-p)^{n-1}\)です。こうして、幾何分布は無記憶性をもつことを証明できました。
また幾何分布は「結果が2つのベルヌーイ試行」に基づいているため、離散型確率分布になります。離散型確率分布の中で、無記憶性があるのは幾何分布だけです。そのため「離散型確率分布での無記憶性=幾何分布」と覚えておきましょう。
幾何分布の性質を理解し、公式の意味を学ぶ
正規分布ほど重要ではないものの、統計学を学ぶときに幾何分布を習うケースがあります。初めて成功する確率が幾何分布であることを理解すれば、幾何分布の確率を計算するのは難しくありません。
ただ幾何分布には2つの定義があるので混乱しやすいです。また期待値や分散を得る公式を出すには、高校数学の計算が必要になります。
さらには、幾何分布には無記憶性があります。離散型確率分布で無記憶性をもつのは幾何分布だけです。そこで、無記憶性がどのような意味をもつのか理解しましょう。
幾何分布を学ぶとき、期待値や分散、無記憶性まで理解する場合、難易度が高くなります。ただ高校数学を理解していれば内容を把握できます。そこで、それぞれの公式が何を意味しているのかを学び、公式の証明を含めて理解しましょう。






