分散分析(ANOVA)の一つに一元配置分散分析があります。複数の群が含まれているとき、差があるかどうか確認する方法が一元配置分散分析(One-way ANOVA)です。
母集団が正規分布しており、調べたい因子が一つの場合は一元配置分散分析が有効です。等分散である必要はありますが、複数の群が含まれていたとしても差があるかどうかを判断できるのです。ただ、具体的にどの群に差があるのか調べることはできません。
なお実際に検定をするとき、一元配置分散分析をするときの手法を理解しなければいけません。公式は難しいものの、理論を学びましょう。
一元配置分散分析を利用すれば、3つ以上の群を含む標本であっても検定できるようになります。そこで、どのように一元配置分散分析を利用すればいいのか解説していきます。
もくじ
因子が一つで対応がないのとき、3群以上を調べる一元配置分散分析
分散分析(ANOVA)の中でも、因子が一つであり、3群以上を調べるときに利用されるのが一元配置分散分析です。最も利用される検定法としてt検定があります。t検定は2群を比較し、差があるかどうかを調べることができます。それに対して、一元配置分散分析では3群以上を含む標本を調べるのです。
「3群以上を含む標本」については理解できると思います。それでは、「因子が一つ」とはどういう意味なのでしょうか。
例えば「湖の汚染度を調べるため、3カ所で水を採取した」とします。このときは同じ湖で水を採取しており、因子が一つです。そこで一元配置分散分析を利用することによって、特定の場所の汚染度が高いかどうかを判断できます。
一方で「運動能力の差について男女で調べる」という場合、運動能力と男女のように因子が二つあります。この場合、一元配置分散分析を利用してはいけません。
いずれにしても、因子が一つのときに利用できる検定法が一元配置分散分析です。なお一元配置分散分析で有意差があるとわかっても、具体的にどのグループ間に差があるのかはわかりません。以下のパターンのうち、どれに該当するのかまではわからないのです。
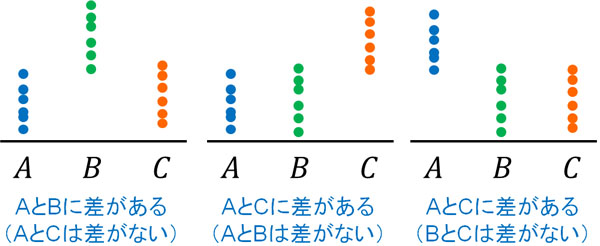
そのため一元配置分散分析で有意差が出た場合、次はそれぞれのグループ間について2標本t検定をします。このときは多重比較法(ボンフェローニ法など)を活用し、P値の補正をすることによって、どのグループ間で差があるのか解析するのです。
なお2標本t検定の中でも、対応のない2標本t検定に相当するのが一元配置分散分析です。対応のない群を3つ以上含む場合、一元配置分散分析が利用されます。
バートレット検定にて、等分散の確認が必要なパラメトリック検定
なお一元配置分散分析を利用する場合、データが等分散している必要があります。等分散というのは、要はデータの形が同じであるかどうかを指します。もしデータの形が等しくない場合、不等分散となります。
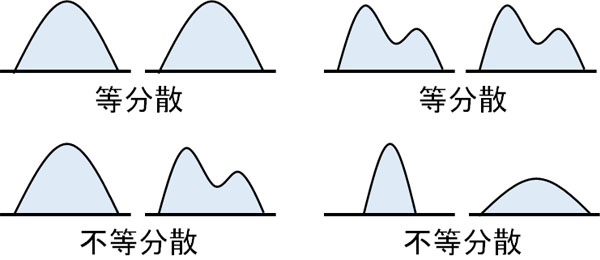
つまり一元配置分散分析を利用するためには、母集団が正規分布していることに加えて、標本が等分散でなければいけません。
3群以上のデータを含む標本について、等分散かどうかを確認する検定法にバートレット検定があります。そのため一元配置分散分析を行う前は必ずバートレット検定をする必要があります。バートレット検定をして等分散であることを確認した後、一元配置分散分析を行うのです。
F分布(F値)を利用し、分散を確認するのが一元配置分散分析
それでは、一元配置分散分析を行うには具体的にどのようにすればいいのでしょうか。分散分析では難しい公式を利用することになります。ただ公式を覚える必要はなく、計算の方法や一元配置分散分析の理論を理解できれば問題ありません。
私たちは数学者ではないため、計算方法を覚える必要はありません。統計処理するときの理論を理解できればいいのです。
一元配置分散分析では分散を利用して検定します。このとき同じ母集団から標本として取り出す場合、当然ながら分散は等しくなります。そのため一つの要因を利用して分類された群について、帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:それぞれの群に差はない(同じ母集団から取り出された標本である)
- 対立仮説:それぞれの群に差がある(異なる母集団から取り出された群が混じっている)
例えば同じ湖の水を採取する場合、通常であれば水の汚染度は同じです。つまり、分散は同じです。ただ同じ湖であっても、隣に工場があるエリアの場合、その場所では湖の汚染度が高くなっているかもしれません。この場合は工場による影響が加わり、母集団(ほかのエリアの水)とは異なる結果を得られます。
他のグループと比べ、明らかに異なる値がデータに含まれている場合、グループ間に差があると判断できます。
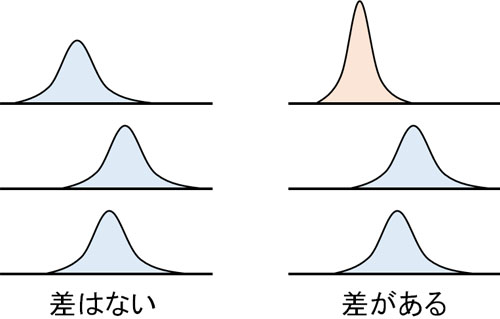
母集団に対して、異なる値が含まれているかどうかを確認する方法が一元配置分散分析です。
なお一元配置分散分析ではF分布を利用します。分散が完全に等しい場合、F値は1になります。一方で異なる分散が含まれている場合、F値は大きくなります。
一元配置分散分析で群間変動と群内変動(誤差変動)を求める
それでは、どのようにしてF値を求めればいいのでしょうか。一元配置分散分析では、以下の公式によってF値を計算します。

「一つの要因について、それぞれの群でどれだけの変動があるのか」を表すのが群間分散です。
ただ分散には、それぞれの群がもつ分散も存在します。これを群内分散といいます。そこで誤差である郡内変動を考慮するため、群間変動に対して群内変動で割るのです。
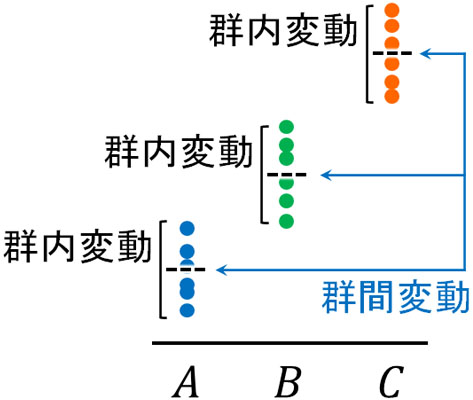
つまり、以下のように考えましょう。
- 群間変動;群に関する平均値のばらつき
- 群内変動:一つの群ついて、測定誤差によるばらつき
そのため分散分析とは、より正確にいうと分散を分析する手法ではありません。分散を利用することによって、平均値を比較する手法です。
同じ母集団からデータを抽出する場合、平均値は同じです。ただ異なる母集団のデータが含まれている場合、それぞれの群を比べたとき、分散が大きくなります。これはつまり、それぞれの群で平均値が異なることを意味します。
公式を利用し、一元配置分散分析の計算を行う
それでは、実際に公式を利用して一元配置分散分析の計算をしてみましょう。実際に計算を行うのは表計算ソフトであっても、教科書で統計学を学ぶときは公式を確認するのが一般的です。
例として、以下の問題を解いてみましょう。
- ある湖について4地点(A~D)で水を採取し、汚染度を調べたところ以下の結果を得られました。群間に差はあるでしょうか。
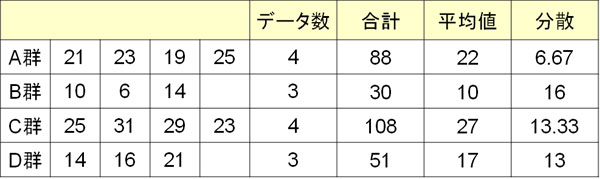
この表のように、一元配置分散分析をするときはデータ数、合計、平均値、分散(不偏分散)をまとめましょう。これにより、その後の計算を行いやすくなります。また帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:それぞれの群の汚染度に差はない
- 対立仮説:それぞれの群の汚染度に差がある
そこで、実際に計算してみましょう。なお、バートレット検定によって「等分散である」と確認されている前提で話を進めていきます。
・群間変動(偏差平方和SA)を計算する
まず、群間変動(偏差平方和SA)を求めます。以下の公式によって群間変動を計算できます。
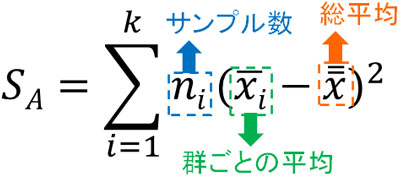
群ごとの平均から総平均を引き、二乗します。その後にデータ数をかけ、すべての群を足しましょう。なお総平均というのは、それぞれの群の平均値を足して割った値ではありません。つまり、\(\displaystyle\frac{22+10+27+17}{4}=19\)ではありません。
そうではなく、セルにあるすべての値を足した後、セル数で割ることによって、総平均を出しましょう。総平均を計算すると、19.79になります。
\(\displaystyle\frac{88+30+108+51}{14}≒19.79\)
そこで、以下のように群間変動(偏差平方和SA)を計算します。
\(S_A=4(22-19.79)^2\)\(+3(10-19.79)^2\)\(+4(27-19.79)^2\)\(+3(17-19.79)^2\)
\(S_A=538.36\)
こうして、群間変動(偏差平方和SA)は538.36とわかりました。また群間変動の自由度dAは群数に対して1を引きます。今回は群の数が4であるため、群間変動の自由度dAは3です。
なお群間変動の分散\((s_A)^2\)は群間変動(偏差平方和SA)と自由度dAを利用して、以下の公式によって求められます。
\((s_A)^2=\displaystyle\frac{S_A}{d_A}\)
そのため、群間変動の分散は179.45です。
\((s_A)^2=\displaystyle\frac{538.36}{3}≒179.45\)
・群内変動(誤差変動:偏差平方和SE)を計算する
次に群内変動(偏差平方和SE)を求めましょう。群内変動は以下の公式によって計算できます。
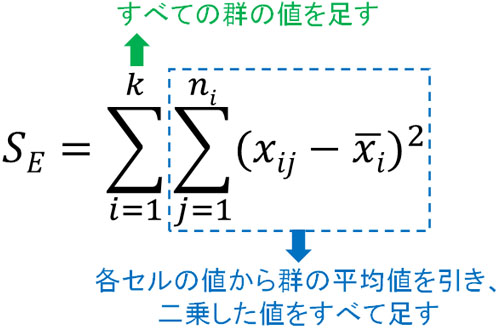
今回の問題では、以下のように計算します。
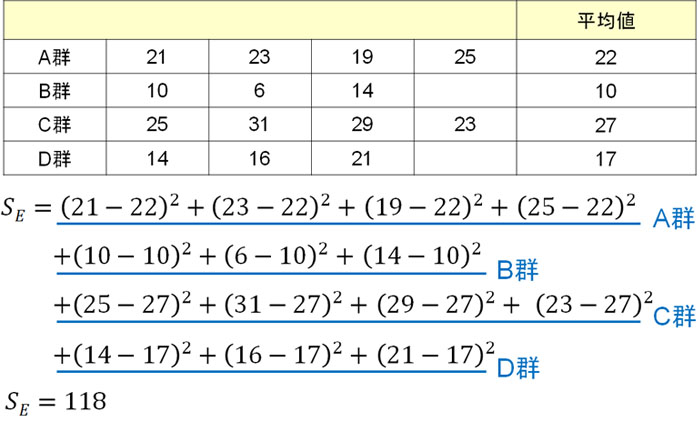
こうして、群内変動SEを得ることができました。なお群内変動の自由度dEは全データ数Nと群数kを利用し、\(d_E=N-k\)で計算できます。そのため、群内変動の自由度dEは10です。
\(d_E=14-4=10\)
なお群内変動の分散\((s_E)^2\)は群内変動SEと自由度dEを利用して、以下の公式によって求められます。
\((s_E)^2=\displaystyle\frac{S_E}{d_E}\)
そのため、群内変動の分散は11.8です。
\((s_A)^2=\displaystyle\frac{118}{10}=11.8\)
分散分析表に自由度、分散、分散比を記す
こうして群間変動と群内変動について計算したら、表(分散分析表)にまとめましょう。以下のように、群間変動と群内変動について自由度、分散、分散比を記すのです。

前述の通り、群間分散\((S_A)^2\)に対して群内分散\((S_E)^2\)で割ることによってF値を得ることができます。そこで群間変動と群内変動について、それぞれ分散を計算した後、分散比を求めましょう。
今回の場合、分散値(F値)は15.21です。この値を得ることによって、それぞれの群で差があるのかどうかを判断できます。
F分布表を利用し、自由度と有意水準を使ってF値を比較する
それでは、今回のF値は有意差があるのでしょうか。F分布表を利用することによって確認してみましょう。
自由度\(d_A=3\)、自由度\(d_E=10\)のとき、有意水準を0.05(5%)となるF値はいくらでしょうか。統計学の教科書を開いてF値を確認すると、3,71であるとわかります。
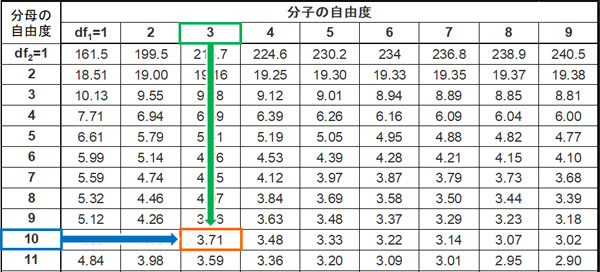
つまりF値が3.71よりも大きい場合、5%以下で起こる稀な現象が発生していると判断できます。
そこで先ほど計算した分散比(F値)を確認すると15.21です。つまりF値が3.71よりも大きく、稀な現象が発生しています。そこで帰無仮説を棄却し、対立仮説を採用します。こうして、湖から採取した水は汚染度に差があると判断できます。
なお実際には、この後に多重比較をします。2標本t検定と多重比較法を利用し、どの群に差があるのか突き止めるのです。前述の通り、一元配置分散分析ではどのグループ間で差があるのか判断できないからです。こうして、より詳細にデータを解析していきます。
因子が一つのデータで利用される多群のパラメトリック検定
標本が3群以上を含み、因子が一つであり、母集団が正規分布する場合は一元配置分散分析を利用して検定します。これにより、それぞれの群に差があるかどうかを見極めることができます。対応のない二標本t検定に該当するのが一元配置分散分析です。
母集団が同じ場合、差がないと判断されます。ただ異なる母集団から取り出されたデータが含まれている場合、平均値が変わります。そこで分散を利用し、差があるかどうかを確かめるのです。
どの群に差があるのか具体的に知ることはできません。そのため一元配置分散分析によって差があるとわかった場合、多重比較法によってさらなる解析が必要になります。
いずれにしても、こうして多群の解析をしていきます。3群以上を含む場合は一元配置分散分析が有効です。分散分析(ANOVA)で必ず学ぶのが一元配置分散分析であるため、どのような理論によって検定するのか理解しましょう。






