統計データの解析するとき、四分位数が利用されます。データの範囲を確認する指標の一つが四分位数です。
統計データでヒストグラムが左右対称の状態(正規分布)でないと利用できない指標はたくさんあります。一方、四分位数はすべてのデータで利用できます。中央値を活用するのが四分位数であるため、データの形に関係なく利用できるのです。
また四分位数を学べば、四分位範囲や四分位偏差を理解できます。これらを利用すれば、データのばらつき(散らばり)がわかります。またこれらの指標を利用することで、箱ひげ図を描くことができます。箱ひげ図により、データの範囲やばらつきを一目で確認できるようになります。
統計学で重要な指標が四分位数や四分位範囲、四分位偏差です。そこで四分位数に加えて、箱ひげ図の利用法を含めて解説していきます。
もくじ
データのばらつきと範囲:最小値と最大値
統計学を学ぶとき、データのばらつき(散らばり)と範囲について理解しましょう。また、データには最小値と最大値があります。最小値と最大値の間を範囲といいます。
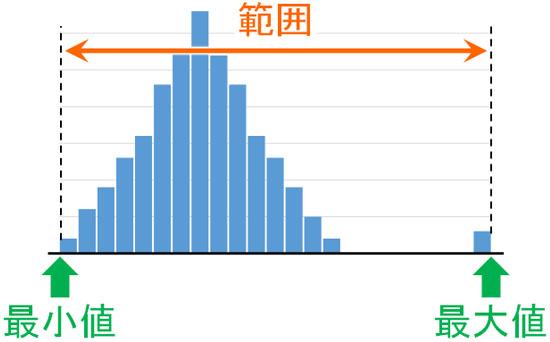
範囲というのは、どれだけデータの散らばりがあるのかを表す指標です。ヒストグラムで確認すると、以下が最小値や最大値、範囲になります。

最小値と最大値については、簡単に理解できると思います。
四分位数を学ぶ:第1四分位数、第2四分位数、第3四分位数
ただ、最小値や最大値を利用しても正しくデータを解読できないケースが多いです。平均値が役に立たないケースが多いのと同じように、最小値・最大値を与えられたとしても正しくデータを読み解くことができないのです。
例えば以下のように、異常値を含むヒストグラムでは最大値が非常に大きくなります。
この場合、データの範囲や最大値を確認したとしても、データを正しく解析できません。そこで、四分位数を利用します。中央値と考え方が似ており、データを四等分する値を四分位数といいます。
四分位数には第1四分位数(Q1)、第2四分位数(Q2)、第3四分位数(Q3)があります。
- 第1四分位数:データのうち、25%の位置にある数
- 第2四分位数:データのうち、50%の位置にある数(中央値)
- 第3四分位数:データのうち、75%の位置にある数
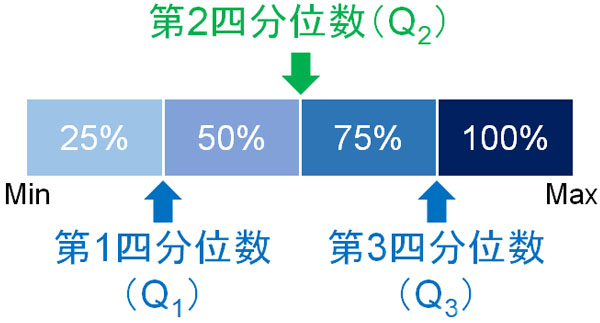
第2四分位数(Q2)というのは、要は中央値のことです。また第1四分位数(Q1)については、上の図で左半分にあるデータの中央値を指します(Q2の値は除く)。第3四分位数(Q1)では、上の図で右半分にあるデータの中央値を指します(Q2の値は除く)
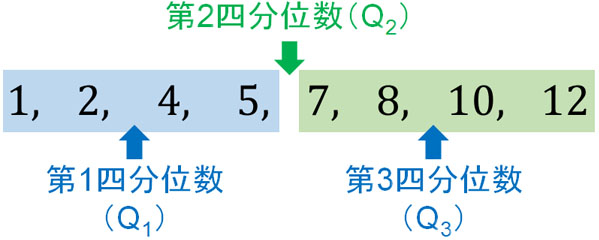
例えば、データの数が奇数である以下のデータについて四分位数を求めてみましょう。
- 1, 2, 4, 5, 7, 8, 10
第1四分位数(Q1)、第2四分位数(Q2)、第3四分位数(Q3)はそれぞれ以下のようになります。

こうして第1四分位数(Q1)は2、第2四分位数(Q2)は5、第3四分位数(Q3)は8とわかります。データを小さい順から並べた後、中央値を見つけましょう。その後は中央値を除き、左半分のデータと右半分のデータについてそれぞれ中央値を出します。これにより、四分位数を出すことができます。
一方でデータの数が偶数の場合、どのように四分位数を出せばいいのでしょうか。この場合、中央値と同様に計算が少し複雑になります。以下のデータを例に考えてみましょう。
- 1, 2, 4, 5, 7, 8, 10, 12
真ん中にある2つの数字の平均値を出すことによって、中央値を出すことができます。真ん中の数字は5と7であるため、第2四分位数(Q2)は6です。
また左半分のデータの中央値を出すと、第1四分位数(Q1)を得ることができます。左半分のデータの真ん中にある数字は2と4なので、第1四分位数(Q1)は3です。
第3四分位数(Q3)を得るときについても計算方法は同じです。右半分のデータの真ん中にある数字は8と10です。そのため、第3四分位数(Q3)は9です。
四分位範囲は25~75%の範囲を表す
なお四分位数の計算方法を学べば、四分位範囲と四分位偏差を理解できるようになります。四分位範囲の概念は難しくなく、25%(Q1)から75%(Q3)の範囲を四分位範囲といいます。
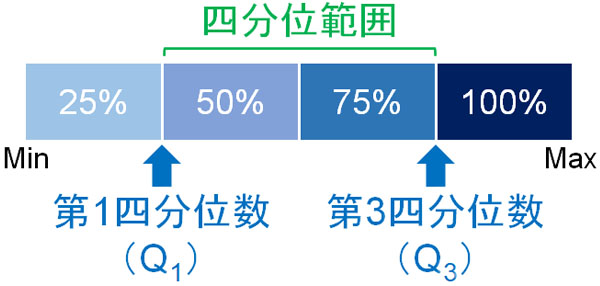
25~75%の範囲が四分位範囲であるため、四分位範囲には必ず50%のデータが入ります。また、四分位範囲は以下の式によって求めることができます。
- \(Q_3-Q_1\)
四分位範囲では中央値を利用するため、グラフが正規分布になるかどうかに関係なく、すべてのデータで有効な指標です。
四分位偏差を利用し、データのばらつきを確認する
なお四分位範囲が大きいというのは、何を意味しているのでしょうか。データのばらつきが小さい場合、四分位範囲の値は小さくなります。一方でデータのばらつきが大きい場合、四分位範囲の値は大きくなります。
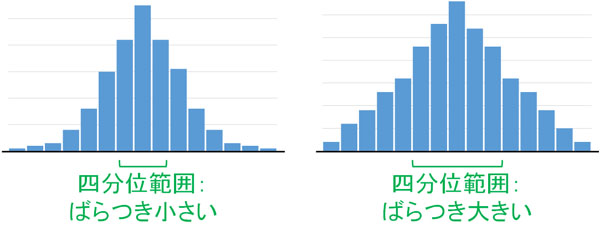
統計データのばらつきを表す言葉に偏差(へんさ)があります。データのばらつきを表す指標としては、標準偏差が広く利用されています。ただ異常値(外れ値)が多い場合、標準偏差は利用できません。
一方で前述の通り、すべてのデータで四分位範囲が有効です。中央値を利用するのが四分位範囲であるため、異常値を外すことができるのです。そこで四分位範囲を利用し、データのばらつきを確認する指標が四分位偏差です。
四分位偏差を出すときでは、四分位範囲の値を2で割りましょう。四分位範囲は「\(Q_3-Q_1\)」で求めることができるため、四分位偏差は以下の式によって計算できます。
- \(\displaystyle\frac{Q_3-Q_1}{2}\)
四分位範囲を理解していれば、四分位偏差を得るのは難しくありません。
四分位偏差では、なぜ四分位範囲を半分にするのか
それでは、なぜ四分位偏差を出すときに2で割るのでしょうか。この理由を理解しないと、なぜ四分位偏差がデータの散らばりを表すのか理解することができません。
まず\(\displaystyle\frac{Q_1\color{red}{+}Q_3}{2}\)によって、第1四分位数(Q1)と第3四分位数(Q3)を足して2で割る場合、中央値(メジアン)を得ることができます。25%と75%を足すと100%であり、半分にすると中央値になるのです。
一方で\(\displaystyle\frac{Q_3\color{red}{-}Q_1}{2}\)によって、第3四分位数(Q3)から第1四分位数(Q1)を引いて2で割る場合、前述の通り四分位偏差を得ることができます。
それでは、以下の式はどのようになるでしょうか。
- 中央値 \(±\) 四分位偏差
中央値は\(\displaystyle\frac{Q_1+Q_3}{2}\)であり、四分位偏差は\(\displaystyle\frac{Q_3-Q_1}{2}\)です。そこでこの式を計算すると、以下のようになります。
- 中央値 + 四分位偏差 = 第3四分位数(Q3)
- 中央値 – 四分位偏差 = 第1四分位数(Q1)
このように中央値と四分位偏差を利用することによって、第1四分位数(Q1)と第3四分位数(Q3)を得ることができます。つまり、四分位偏差は「中央値(50%)から25%や75%まで、どれだけデータにばらつきがあるのか」を表しています。
四分位偏差が統計データのばらつきを表しており、何を意味しているのか理解すれば、なぜ四分位範囲を半分にすることで四分位偏差を得られるのか理解できるようになります。
箱ひげ図は何を表すのか
ここまで四分位数や四分位範囲、四分位偏差について解説してきました。これらを学べば、箱ひげ図を理解できるようになります。
箱ひげ図とは、以下の図を指します。
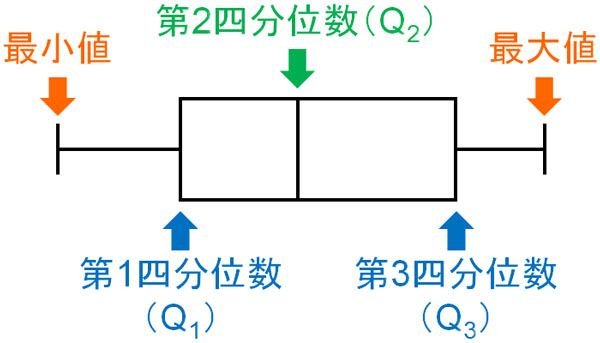
このように、一つの図によって最小値や最大値、第1四分位数(Q1)、第2四分位数(Q2:中央値)、第3四分位数(Q3)を表すのが箱ひげ図です。
最小値や最大値、四分位数はデータの範囲を表します。また、四分位範囲はデータのばらつきを表します。つまり箱ひげ図とは、「データにどれだけ散らばりがあるのか」を見た目で判断できるようにするツールです。
また箱ひげ図を確認すれば、四分位範囲を簡単に判断できます。四分位範囲には50%のデータが含まれているため、半分のデータがどこに分布しているのかわかります。中央値についても箱ひげ図で確認できるため、データの大まかな概要がわかるのです。
箱ひげ図の形と外れ値を含むケース
統計データの値によって、当然ながらヒストグラムの形が変わります。またヒストグラムの形が違うと、箱ひげ図の形も変化します。
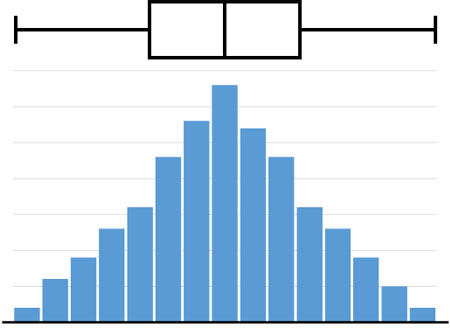
ヒストグラムの形が左右対称であり、正規分布しているデータでは以下のような箱ひげ図になります。
一方、異常値を多く含むヒストグラムだと箱ひげ図はどのようになるのでしょうか。異常値を含む場合、正規分布に従うデータに比べて、箱ひげ図の形は以下のように変化します。
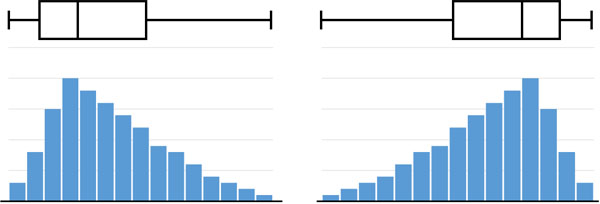
なおデータの中には、非常に大きい値(または小さい値)を含むことがあります。その場合、箱の大きさは変わらないものの、最大値や最小値の値が非常に大きく(または小さく)なります。
例えば平均年収を調べるとき、データの中にたまたま大富豪が含まれているとどうでしょうか。箱ひげ図を描くと、最大値が非常に大きくなってしまいます。
統計データでは人間によるミスや測定機器のエラーなど、さまざまな理由によって外れ値を含んでしまうケースがあります。こうした異常値を排除しなければいけません。そこで箱ひげ図を描くとき、「最大値と最小値は四分位範囲(箱の範囲)に対して1.5倍までの長さにする」ことがよくあります。
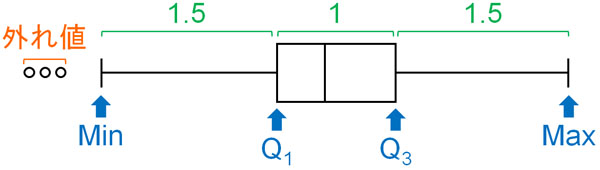
この場合、箱ひげ図に入らないデータが出てきます。箱ひげ図の外にデータがある場合、それは外れ値を表しています。
都合の悪いデータを外れ値にして、意図的に排除してはいけません。ただ場合によっては、グラフを描くときに異常値を排除することが有効になるケースがあるのです。
データの形に依存せず、範囲やばらつきを確認する
統計データを解析するとき、データが正規分布に従っていなかったとしても利用できる指標として四分位数があります。
データの最小値と最大値を確認した後、データを四等分するのが四分位数です。四分位数がわかれば、四分位範囲がわかります。四分位範囲を確認すれば、データの50%がどこに分布しているのかわかります。また四分位偏差により、データのばらつきがわかります。
これらを理解すれば、箱ひげ図を描けるようになります。データの範囲や散らばりを見た目で判断できるツールが箱ひげ図です。ただ異常値がある場合、箱ひげ図の外に外れ値を記すことがあります。
データの形に依存せず、データの範囲やばらつきを確認できるツールが四分位数や四分位範囲、四分位偏差、箱ひげ図です。統計学を学ぶとき、これらのツールを利用できるようにしましょう。






