統計では先入観をできるだけ排除することが重要になります。実験をするとき、都合の良いデータが出てしまうことがあります。これは、実験データに先入観が含まれているからです。これをバイアスといいます。
そのためバイアスを排除することにより、正しい研究データを得なければいけません。そのために必要な操作が無作為化や盲検化です。
特に医療統計では、無作為化や盲検化が頻繁に利用されます。もちろん医療統計に限らず、一般的な実験操作であっても無作為化や盲検化を行い、正しい実験データを得られるようにしなければいけません。
それでは、どのようにしてバイアスを排除すればいいのでしょうか。ここでは無作為化や盲検化の考え方を解説していきます。
もくじ
先入観によって結果が変化する
正しい実験データを得るためには、できるだけ先入観を排除しなければいけません。実際のところ、先入観によって結果が大きく変化するからです。
例えば薬を飲むとき、医師が「この薬は非常によく効きます」と伝え、偽薬(プラセボ)を渡す場合、患者の症状は大きく改善することが広く知られています。実際には効果がなくても、思い込みによって症状が改善してしまうのです。これを医療ではプラセボ効果といいます。
統計でのバイアスというのは、思い込みや先入観を意味します。バイアスが加わることによって、本来は有意差がないにも関わらず、有意差があると判断されてしまうのです。統計学では、以下の種類のバイアスがあります。
- 情報バイアス
- 選択バイアス
- 交絡バイアス
それぞれの種類について学んでいきましょう。
情報バイアスは最も一般的な統計ミス
最も一般的であり、実験ミスが発生しやすいのが情報バイアスです。つまり、事前に情報を与えられることによって偏った統計データを得られるのです。先ほどのプラセボ効果は情報バイアスの一つになります。
実験をするとき、情報バイアスを必ず避けましょう。例えば2つのワインを用意し、飲み比べをするとします。一つは1本10万円のワインAであり、もう一つは1本2000円のワインBです。事前にワインの値段を教える場合、高確率で多くの人が「10万円のワインのほうがおいしい」と答えます。
ただ実際のところ、ワインの味に詳しい人は少ないです。そのため事前に情報を与えずにワインの試飲をすると、人の意見は分かれます。
情報バイアスはあらゆる場面で存在します。統計データを取るとき、情報バイアスがあると標本データ自体が不正確であり、使えないデータが集まります。何も対策をしない場合、すべてのデータで情報バイアスが発生すると考えましょう。
選択バイアスにより、ダメな標本が作られる
バイアスには選択バイアスも存在します。つまり、どのような基準で標本を集めるのかによって結果が変わるというわけです。
例えば新開発の運動靴の性能を試すとき、本来であればランダムに人を集めなければいけません。ただスポーツ選手のみを集めて新開発の運動靴を履かせる一方、比較対象の運動靴の群については太っている人を集めて履かせます。この場合、新開発の靴は明らかに良い結果がでます。
ただ優れた結果を得られたとしても、新たな運動靴の性能が優れているから有意差が表れたわけではありません。運動能力の違う人を集めたため、有意差が出たというわけです。研究計画の段階でミスがあると、選択バイアスによって実際とは異なる結果を得られます。
なお選択バイアスは多くの場面で私たちが経験しています。例えばマスメディアが行う政治での支持率は基本的に役に立ちません。事実、メディアによって支持率はまったく違います。これは「どの属性の人を対象に抽出してアンケートを取るのか」によって意見がまったく異なるからです。
交絡バイアスがあると正しい研究結果を得られない
他に注意しなければいけないバイアスが交絡バイアスです。ほかの因子によって結果が変わる場合、交絡バイアスが発生しているといえます。
例えば肺がんと性別について調べたとします。その結果、明らかに男性のほうが肺がんの発症率が高いとわかりました。この場合、「男性は女性よりも肺がんの発生率が高い」と結論付けていいでしょうか。
ただ実際には、この結論は間違っています。理由としては、一般的に女性よりも男性のほうが喫煙率が高いからです。つまり、喫煙という交絡バイアスが含まれることによって得られた結果といえます。そのため、本来は以下のようになります。
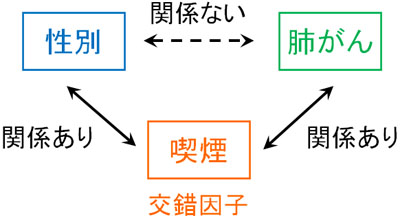
交錯因子の存在によって、本来は関係がなかったとしても、一見すると関係ありそうなデータを得られてしまうケースがあります。今回はわかりやすい例を記しましたが、いずれにしても第三の要因によって結果が変わってしまうことがあるのです。
交錯バイアスまで考慮すると、すべてのバイアスを完ぺきに回避するのは不可能です。ただ実際に研究データを集めるとき、交錯バイアスについてもできるだけ排除しなければいけません。
統計でのバイアスを回避するための方法
こうしたバイアスについて、医療統計では絶対に考慮しなければいけません。ただ当然ながら、その他の研究でも可能な限りバイアスを避ける必要があります。バイアスを避ける対策を最も高度にしているのが医療統計であり、医療統計で行われている対策を真似することでバイアスを回避しやすくなります。
それでは、どのようにして統計でのバイアスを回避すればいいのでしょうか。前述の通り100%回避するのは不可能であるものの、以下の方法を利用することによって対策できます。
- 無作為化(ランダム化)を行う
- 二重盲検化により情報バイアスをゼロにする
- 層別解析を行う
それぞれの方法を解説していきます。
無作為化(ランダム化)によって実験を行う
バイアスを抑える初歩として無作為化(ランダム化)を行わなければいけません。無作為化とは、均等になるようにサンプルを振り分けることを指します。無作為化を行う理由としては、選択バイアスをなくす必要があるからです。
例えば新製品を利用してテストをするとき、新製品を利用する群ではプロばかりであり、もう一方の対象群が旧製品を利用する一般人の場合、製品の結果に差が出るのは当然です。つまり、製品の性能を正しく判定することはできません。
そこで選択バイアスを可能な限りゼロにするため、対象を選ぶとき、ランダムに振り分けるようにしましょう。標本の中にプロと素人がいるのは問題ありません。製品の利用群と比較対象の群について、ランダムに割り当てるのです。これを無作為化(ランダム化)といいます。
「特定のルールに沿って割り当てる方法」が無作為化です。いずれにしても、調べたい群と対象群について、ランダムに割り当てなければいけません。
単盲検化・二重盲検化(ダブルブラインド)によってプラセボ対策をする
次に情報バイアスを排除しましょう。実際に実験を行うとき、事前に情報を与えるとほぼ確実に情報バイアスが発生します。
医療統計では情報バイアスを排除する仕組みが確立されており、薬の効果を確かめる治験(臨床試験)をするとき、患者は新薬を服用しているのか、それともプラセボ(偽薬)を服用しているのか知らされません。これにより、プラセボ対策が可能です。
テスト対象の人に対して、情報を教えずに研究することを単盲検化といいます。
ただ、この方法では不十分です。どちらがプラセボなのか医師が知っている場合、医師は無意識に「(この薬はプラセボではないので)よく効く新薬ですよ」と患者に伝えるかもしれません。こうして、情報バイアスが発生します。
そこですべての臨床試験では、医師についても「どれが新薬であり、どれがプラセボなのか」を知らせないようにします。当然、製薬企業の調査員もどれがプラセボか知りません。知っているのは製薬企業の統計分析チームのみです。
実際の実験を行う人に対して、どの試験をしているのかまったくわからない状態にすればプラセボ対策が可能です。このように、実験する側と実験される側の両方に対して情報を隠し、研究する方法を二重盲検化(ダブルブラインド)といいます。
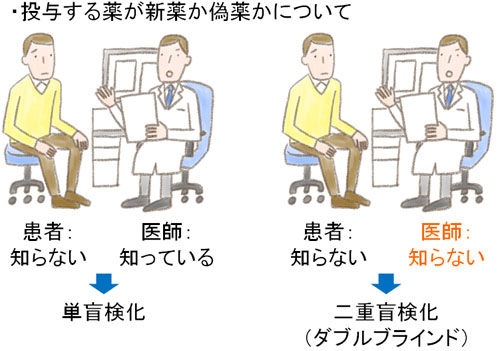
医療統計だけでなく、二重盲検化はすべての実験で効果的です。多くの場合、データの測定者はすべての情報を知っています。ただこの状態だとほぼ100%の確率で情報バイアスが発生します。
そこで、実験の準備をする人と測定者を別の人にしましょう。実験の準備をする人はデータを集める測定者に対して、どれが製品利用群であり、どれが比較対象群なのか知らせずに実験をさせます。これであれば、より正確な実験データを得ることができます。
層別解析で群ごとの影響を確認する
次に、データ取得後に起こるバイアスや交錯バイアスを少なくしましょう。統計解析する方法によっては、交錯バイアスを回避できます。
統計解析の方法によって交錯バイアスを回避する方法はいくつかあります。その中でも最も簡単な方法が層別解析です。層別解析では、以下のように母集団を属性(層)ごとに分けて調査します。
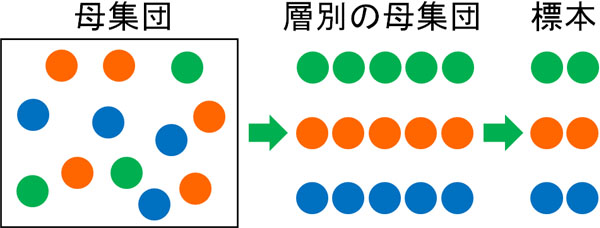
標本を確認すると、複数の属性に分けられることは多いです。例えば性別(男性と女性)や年齢など、分けるときの要素は無数に存在します。
例えば、集中力の持続に効果的なメガネをあなたが開発したとします。このとき標本を以下のように分けて解析しました。
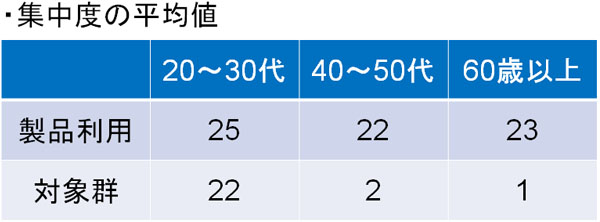
このように年齢によって分けることによって、明らかに結果が異なるとわかります。20~30代の場合、製品を利用しても利用しなくても集中度に大きな違いはありません(製品利用は25、製品を使っていない対象群は22)。一方で40歳以上の場合、衰えていた集中度を回復させることができるとわかりました(40~50代だと製品利用で22、製品を使っていない対象群で2)。
この場合、交錯因子として年齢が存在するとわかります。集めた標本を群ごとに分けない場合、交錯因子を見つけることができません。ただ統計解析の方法によっては、交錯バイアスを見つけることができるのです。
このように交錯因子を発見すれば、どのようなマーケティング戦略を取ればいいのかわかります。例えば先ほどの特殊なメガネであれば、若い人を無視して、40歳以上の人に絞って製品の宣伝をすればいいとわかります。
なお標本のサンプル数が数百以上と多い場合、層別解析が有効です。ただサンプル数が少ない場合、層別解析をすることができません。つまりサンプルが少ないと、統計解析による交錯因子の発見を諦める必要があります。統計データの解析では、サンプル数が多いほど良いのはこうした理由もあります。
データを集めるとき、バイアスを避けるべき
研究データを集めるとき、何も対策をしないと100%の確率でバイアスが加わります。つまり、正しくないデータを得られてしまうのです。情報バイアスや選択バイアス、交錯バイアスなど多くのバイアスがあり、これらを避けなければいけません。
バイアスをすべて避けることはできません。ただ無作為化や二重盲検化(ダブルブラインド)を利用することにより、多くのケースでバイアスを避けることができます。特に医療統計ではバイアスを避ける方法が研究されており、薬の治験では必ず無作為化と二重盲検化を行います。
また交錯バイアスを避けたい場合、統計解析の方法を工夫しましょう。例えば層別解析を行うことにより、交錯因子を見つけることができます。
どのような研究であっても、バイアスが発生することを認識しましょう。そこで、可能な限りバイアスを避けて実験データを集めるといいです。






