統計処理をするとき、2つの標本ではなく、3つ以上の標本を比べることがあります。このとき、それぞれの群について分散が等しいかどうかを確認する方法がバートレット検定です。
統計での検定法の中には、等分散であることを前提としているケースがあります。そのため、事前にバートレット検定をしなければいけないことがあるのです。特に一元配置分散分析と二元配置分散分析法ではバートレット検定が重要になります。
それでは、どのようにバートレット検定を利用して等分散かどうかを確認すればいいのでしょうか。また、どのように公式を利用して計算すればいいのでしょうか。
バートレット検定をするため、原理を理解しましょう。ここでは、バートレット検定の概念や検定法を解説していきます。
もくじ
分散を確認し、データの形が同じかを判断する
バートレット検定とは、複数の標本について等分散かどうかを確認する手法と理解しましょう。等分散というのは、要はグラフの形が同じかどうかを指します。
グラフの形が同じ場合、標本は等分散です。一方でグラフの形が異なる場合、不等分散です。以下のようなイメージになります。
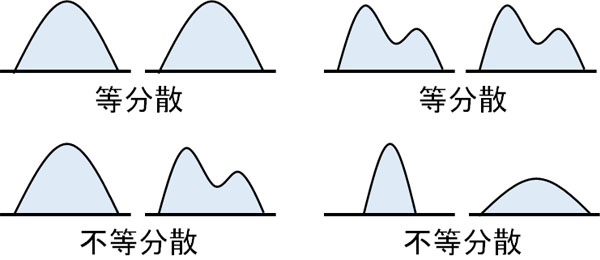
それでは、どのようにして等分散かどうかを見極めればいいのでしょうか。等分散であるかどうかの指標に分散があります。そのためバートレット検定では、分散を利用することによって検定をします。
もちろん、分散が等しくても不等分散であるケースはあります。ただ通常、分散が等しければデータの形が似ていると考えて問題ありません。そのため、等分散かどうかの確認では分散が利用されるのです。
一元配置分散分析と二元配置分散分析で重要なバートレット検定
それでは、なぜグラフの形が同じかどうかを確認することが重要なのでしょうか。この理由として、統計手法の中には「等分散である」ことが前提条件になっているケースがあるからです。
つまり母集団が正規分布しているだけでなく、等分散でなければいけないのです。例えば3群以上の有意差を検定する場合、以下の検定手法が利用されます。
- 一元配置分散分析
- 二元配置分散分析
一元配置分散分析や二元配置分散分析を利用するためには、母集団が正規分布していることに加えて、等分散である必要があります。つまり等分散でない場合、一元配置分散分析や二元配置分散分析などのパラメトリック検定を利用することはできません。
一元配置分散分析や二元配置分散分析など、複数の群が標本に含まれているときに利用する検定法が分散分析です。ただ分散分析として一元配置分散分析や二元配置分散分析を利用する場合、事前にバートレット検定をしなければいけません。
なおバートレット検定によって分散が均一ではないとわかったら、ほかの統計手法を用いて検定しましょう。この場合、母集団が正規分布していなくても利用可能なクラスカル・ウォリス検定やフリードマン検定などのノンパラメトリック検定を利用します。
F検定とバートレット検定の違いは何か
このとき、多くの人が「F検定とバートレット検定は何が違うのか」について疑問に思います。等分散かどうかを確認する検定法には、F検定とバートレット検定があります。この違いについては、以下のように考えましょう。
- F検定:2つの群の等分散を確認する
- バートレット検定:3つ以上の群の等分散を確認する
F検定では2群間の分散が等しいかどうかを確認できます。一方でバートレット検定では、複数の群(3つ以上の群)の分散が等しいかどうかを確認できます。そのため2群の検定をしたいのか、それとも多群の検定をしたいのかによってF検定とバートレット検定を使い分けましょう。
バートレット検定を行う手順
それでは、実際にバートレット検定を利用して多群間の分散を確認するにはどのようにすればいいのでしょうか。分散を確認することで等分散かどうかを判断するため、バートレット検定では当然ながら分散を利用します。
このとき、大まかに以下のような手順になります。
- 各データの分散と全体の分散を計算する
- カイ二乗値(χ2値)を求める
- 有意水準と比較する
F検定ではF値を求めることによって有意水準と比べます。一方でバートレット検定では、自由度\(k-1\)に従うカイ二乗分布になります(\(k\)は群の数)。そこで、カイ二乗値を利用することによって等分散かどうかを確認するのです。
公式を利用し、群内変動を表す分散
それでは、どのようにして全体の分散を計算すればいいのでしょうか。それぞれの群の分散について、計算方法は既に理解していると思います。一方で標本全体の分散については、公式を利用して計算しましょう。
例えば、以下の3つの群があるとします。
| データ | サンプル数 – \(n_k\) | 分散(不偏分散) – \(S_E\) | |
| A | 32, 25, 27, 28, 30, 33 | 6 – \(n_1\) | 10.7 – \((S_1)^2\) |
| B | 20, 24, 18, 25, 26, 22, 28, 23 | 8 – \(n_2\) | 10.5 – \((S_2)^2\) |
| C | 10, 13, 14, 15, 10 | 5 – \(n_3\) | 5.3 – \((S_3)^2\) |
群内変動の分散(群の中での観測値のばらつき)を計算するとき、以下の公式を利用します。
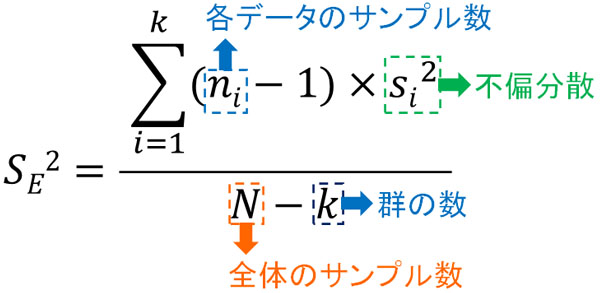
なお、\((S_E)^2\)は群内変動を表す分散です。公式の意味を理解する必要はなく、数学者が導き出した公式を私たちは利用させてもらいましょう。この公式では、それぞれの群のサンプル数と分散(不偏分散)を利用して全体の分散を計算します。
例えば、先ほどの表では以下のように計算します。
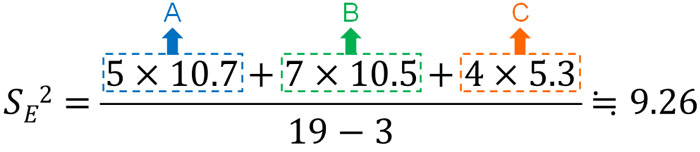
\(Σ\)はすべてを足すことを意味します。そこでそれぞれの群について計算し、足すことによって群内変動を表す分散を計算しましょう。
分散の偏り度と補正係数を求め、統計量を得る
群内変動を表す分散を得たら、次に計算するのが統計量χ2です。カイ二乗値を計算するとき、バートレット検定では以下の2つを求めなければいけません。
- 分散の偏り度M
- 補正係数C
どれだけ分散に偏りがあるのかを表すのがMです。分散の偏り度Mが大きいほど、分散が偏っている(グラフの形が異なる)といえます。
ただ、データ数が多くなると分散の偏り度Mが大きくなる性質があります。そこで補正するため、補正係数Cを利用しましょう。分散の偏り度Mと補正係数Cを得る公式は以下になります。
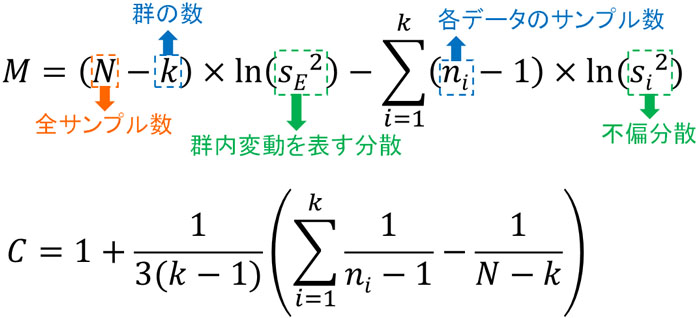
この公式を覚える必要はないものの、公式に数字を代入することで分散の偏り度Mと補正係数Cを得られることを理解しましょう。先ほどの表であれば、以下のように計算できます。
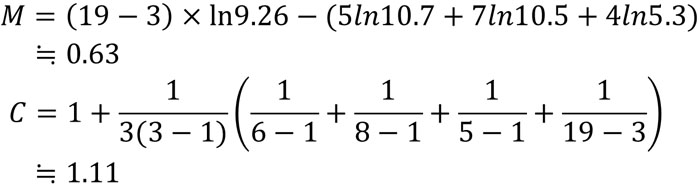
いずれにしてもサンプル数や群数、分散(不偏分散)、群内変動を表す分散を利用することによって分散の偏り度Mと補正係数Cを計算できると理解できれば問題ありません。
次に、カイ二乗値を計算しましょう。分散の偏り度Mと補正係数Cを利用し、以下の公式によって統計量χ2を計算できます。
- \(χ^2=\displaystyle\frac{M}{C}\)
そのため、カイ二乗値は以下のように計算できます。
\(χ^2=\displaystyle\frac{0.63}{1.11}≒0.568\)
カイ二乗分布を利用し、等分散かどうかを確認する
それでは有意水準を0.05(5%)とすると、今回の標本は等分散でしょうか、それとも不等分散でしょうか。帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:分散に差はない(等分散)
- 対立仮説:分散に差がある(不等分散)
前述の通り、バートレット検定では自由度\(k-1\)に従うカイ二乗分布となります。\(k\)は群の数です。今回の群数は3であるため、自由度は2です。そこで統計学の教科書を利用し、自由度2のとき、0.05となるカイ二乗値を見つけましょう。
カイ二乗分布表を確認すると、自由度2ではχ2値が5.991のとき、確率が0.05(5%)となります。つまりカイ二乗値が5.991以上の場合、5%以下で起こる稀な現象が起こっていると判断できます。
ただ先ほど計算したカイ二乗値は0.568であり、0.05(5%)となる5.991よりも値が小さいです。そのため帰無仮説を棄却できず、分散に差はないと判断できます。つまり標本は等分散であり、一元配置分散分析や二元配置分散分析などのパラメトリック検定を利用することができます。
分散分析で重要なバートレット検定
3つ以上の群を検定する方法が分散分析であり、分散分析には一元配置分散分析や二元配置分散分析があります。ただ、これらのパラメトリック検定をする前にバートレット検定が必要になります。つまり、等分散であることの確認が必要です。
公式は複雑であるものの、分散や群の数、サンプル数などを当てはめることによってバートレット検定が可能です。カイ二乗値を確認し、有意差がない場合は等分散であり、有意差がある場合は不等分散と判断できます。
もしバートレット検定をして不等分散であるとわかった場合、クラスカル・ウォリス検定やフリードマン検定などのノンパラメトリック検定を利用しなければいけません。そのため、分散分析を行う前にバートレット検定を行うというわけです。
バートレット検定をするとき、事前に理論を理解しましょう。また分散が等しいかどうかを確認した後、分散分析を行うようにしましょう。






