定常波の式：合成波や自由端反射・固定端反射、定常波の節・腹

高校物理で波動を学ぶとき、合成波を理解することになります。2つの波が合成されるとき、どのような波を生じるのか学ぶのです。

波が反射するとき、自由端反射と固定端反射の2種類があります。両者の違いを正しく理解していない人は多いため、なぜ波の反射に違いを生じるのか把握しなければいけません。

また波の反射などにより、同じ波が重なると定常波を生じます。特定の位置で振動する波が定常波であり、定常波では節と腹を生じます。そこで定常波の形や式を計算できるようになりましょう。

それでは、定常波の性質には何があるのでしょうか。また、定常波の式はどのように計算すればいいのでしょうか。波が重なることによって生じる定常波について解説していきます。

1 波の独立性：重ね合わせの原理と合成波
- 1.1 自由端反射と固定端反射の違い
2 定常波によって生じる節と腹
3 合成波や定常波の式を理解する

波の独立性：重ね合わせの原理と合成波

波には独立性があります。つまり、波同士が衝突することはありません。

2つの物体が衝突する場合、衝突後は物体の速度が速くなったり遅くなったりします。それに対して、波は2つの要素が重なります。つまり、波が重なるときは大きな波になります。そうして時間が経過すると、元の大きさの波となって進行します。

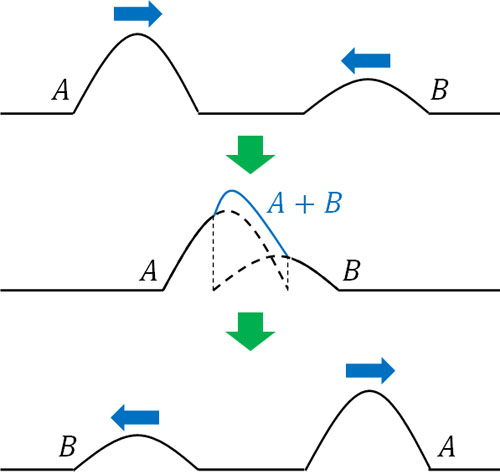
例えば波Aの高さが1mであり、波Bの高さが2mの場合、2つの波が重なると高さは3mになります。このように、波の高さを足し算によって計算できる法則を重ね合わせの原理といいます。また、複数の波が重なっているとき、合成波と呼ばれます。

ただ波には独立性があるため、合成波となったあとは再び元の波形に戻ります。これが、波の合成を考えるときの基本的な概念です。

自由端反射と固定端反射の違い

合成波で重要なのは、波の反射です。波が反射する場合、同じ形の波を生じます。ただ波が反射するとき、以下の2種類があります。

自由端反射
固定端反射

自由端とは、端が固定されていない場合の反射です。例えばロープの端に輪っかをつけ、棒に通します。この場合、横波を起こすと輪っかは壁（\(y\)軸）を自由に移動できます。

このように反射する点が固定されておらず、波の振幅に合わせて\(y\)軸のさまざまな場所で反射する場合は自由端反射といいます。

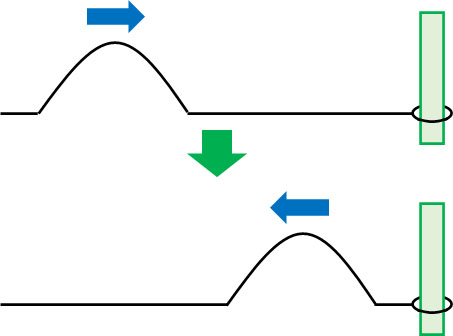
多くの場合、端は固定されていないため、波が壁に反射するときは自由端反射となります。自由端反射の場合、反射によって反対方向に同じ形の波が発生します。

なお壁によって波が反射されるとき、合成波となります。自由端反射では、反射によって同じ形の波が発生するため、壁を鏡と捉え、反射時の波を加えましょう。例えば、以下のようになります。

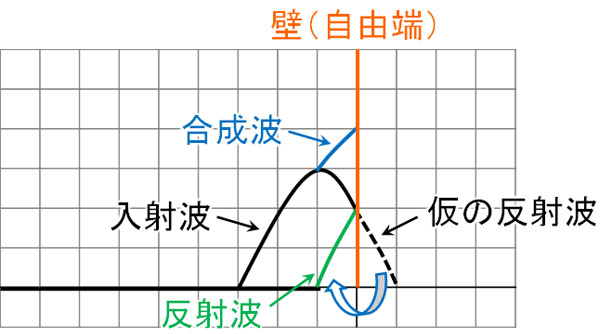
自由端反射では、同じ形の反射波が発生します。そこで壁がないと仮定し、仮の反射波を図に記載しましょう。その後、仮の反射波を反転させ、入射波と反射波を足しましょう。これにより、自由端反射での合成波を作ることができます。

なお自由端反射では、入射波と反射波の変位（\(y\)軸の値）は必ず同じです。そのため、合成波は入射波の変位（または反射波の変位）の2倍になります。

・固定端反射での反射波の形と合成波

一方、固定端反射では端が固定されています。そのため波が壁で反射するとき、必ず\(y=0\)となります。この場合、入射波に対して反射波は反転した形となります。

固定端反射では、壁の変位が必ず0にならなければいけません。そのため入射波を反転させた波が発生するとき、壁では常に\(y=0\)となります。

そのため固定端反射では、壁での波の変位が常に0となるように合成波を作りましょう。以下のように、自由端反射での仮の入射波を反転させることにより、固定端反射での仮の入射波を作ることができます。

その後、固定端反射での反射波を描き、入射波と反射波を合成しましょう。そうすると、合成波を得られます。

定常波によって生じる節と腹

ここまでの内容を理解すれば、定常波を学ぶことができます。定常波が作られるためには、振幅、波長、振動数、波の速さが完全に一致する必要があります。言い換えると、定常波が作られるときはほとんどのケースで反射波が存在する場合です。

入射波と反射波は同じ振幅、波長、振動数、速さであるため、定常波を作ることができるのです。

それでは、定常波とは何なのでしょうか。同じ振幅、波長、振動数、速さをもつ2つの波が合わさる場合、左右に移動せず、上下運動をする合成波を得られます。このような合成波を定常波といいます。以下が定常波です。

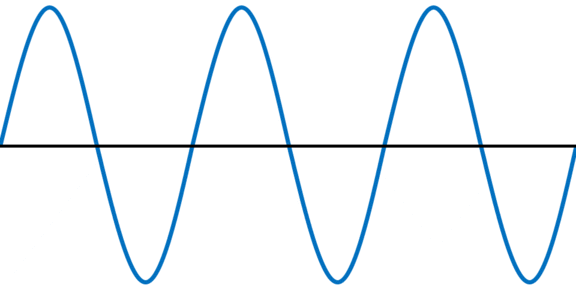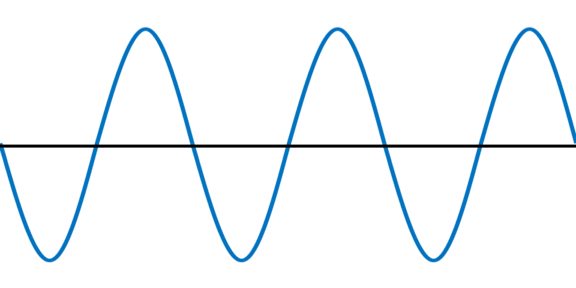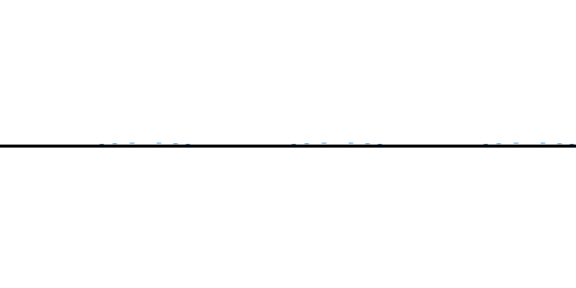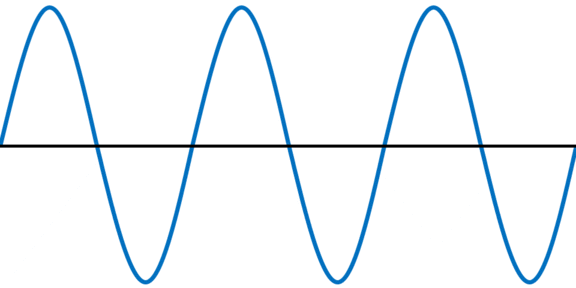
まったく同じ2つの波（入射波と反射波）が反対向きで進行する場合、以下のようになります。

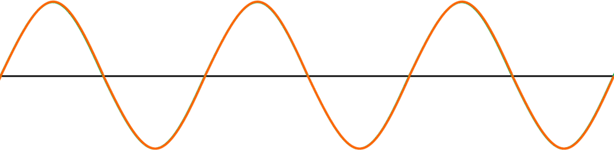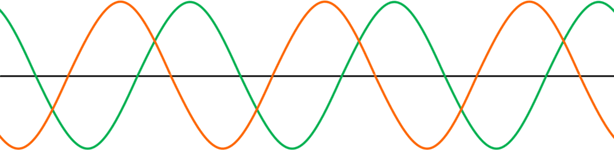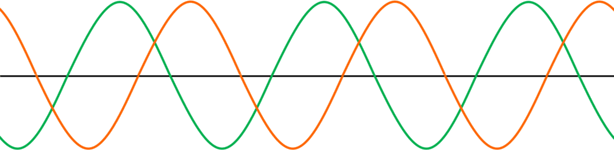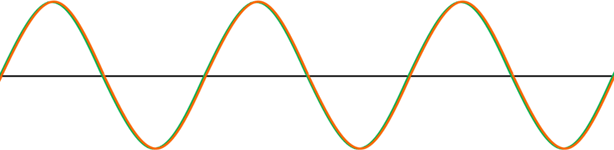
同じ形・速さの2つの波が重なると、合成波は先ほど提示した定常波となります。

定常波は右にも左にも進んでいないように見えます。ただ実際には、形が同一である2つの波が同じ速さで進んでいるのです。

このとき、定常波で振動していない部分を節（ふし）といいます。また、定常波で最も振幅が大きくなっている部分を腹（はら）といいます。

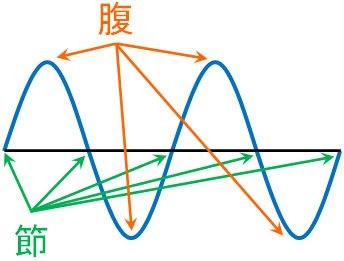
自由端反射では、入射波と反射波が強め合います。そのため、反射点（壁）は必ず腹になります。一方、固定端反射では反射点（壁）の変位は必ず0になります。つまり、固定端反射では反射点が必ず節になります。

原点以外での波の式を得る：原点との距離を考慮する

それでは、定常波の式を計算できるようになりましょう。そのためには、特定の場所での波の高さを知る必要があります。波の性質を学んでいる場合、原点からスタートする正弦波（sinθで表すことのできる波）は以下の式になることを既に理解していると思います。

\(y=Asinωt=Asin\displaystyle\frac{2π}{T}t\)

ただ、この式は原点からスタートするときの\(y\)座標を得る式です。それでは原点以外の点について、式を表すにはどうすればいいのでしょうか。例えば、下図の\(x_1\)について、\(y\)座標を表す式（\(y_1\)の式）はどのように記せばいいのでしょうか。

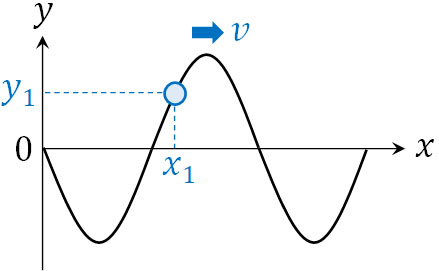
まず、波の速さが\(v\)であり、距離\(x_1\)へ移動するためにかかる時間\(t_1\)を計算しましょう。波は等速で動くため、\(v×t_1=x_1\)と表すことができます。また、式を変形すると以下のようになります。

\(v×t_1=x_1\)

\(t_1=\displaystyle\frac{x_1}{v}\)

つまり\(x=0\)からスタートした後、\(t_1=\displaystyle\frac{x_1}{v}\)秒後に波は\(x_1\)へ到着します。言い換えると、\(x_1\)の位置にある波というのは、\(\displaystyle\frac{x_1}{v}\)秒前には座標（\(0,y_1\)）に存在していたことになります。

理解しやすくするため、具体的な数字で考えてみましょう。

例えば2m/sで進む波について、時刻\(t=10\)sで\(x=6\)mのときの変位を計算しましょう。1秒で2m進むため、6mの場所へ行くには3秒かかります。言い換えると、3秒前（時刻7sのとき）は\(x=0\)の場所に波が存在していたことになります。

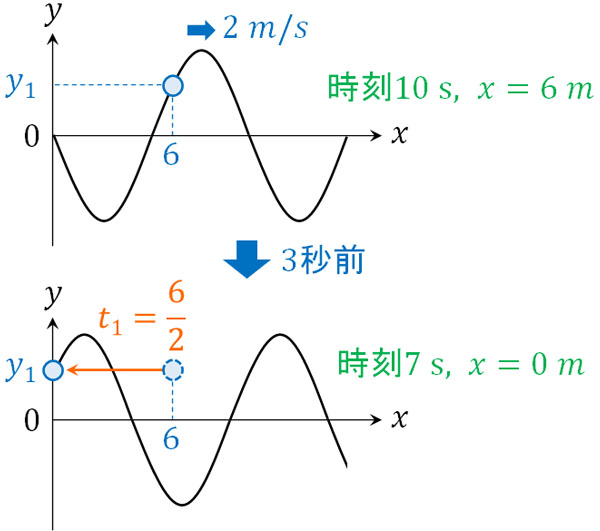
つまり時刻10sで\(x=6\)mの変位を求めるのと、時刻7sで\(x=0\)の変位を求めるのは意味が同じです。

元々の式は\(y=Asinωt\)であり、この式を利用することによって\(x=0\)、かつ時刻\(t=10\)sの\(y\)座標を得られます。\(t=10\)なので、式は\(y=Asin10ω\)です。ただ私たちが知りたいのは、\(x=0\)、かつ時刻\(10-3=7\)sの\(y\)座標です。

そこで、\(y=Asin7ω\)とします。前述の通り、時刻7秒のとき、\(x=0\)の変位を計算すれば、時刻\(t=10\)のときの\(y\)座標を得られます。

次は、これを記号で表しましょう。

時刻\(t\)、\(x=0\)の変位は前述の通り、\(y=Asinωt\)で表すことができます。一方、時刻\(t\)、\(x=x_1\)の変位というのは、\(\displaystyle\frac{x_1}{v}\)秒前（時刻\(t-\displaystyle\frac{x_1}{v}\)秒のとき）では、\(x=0\)に位置します。

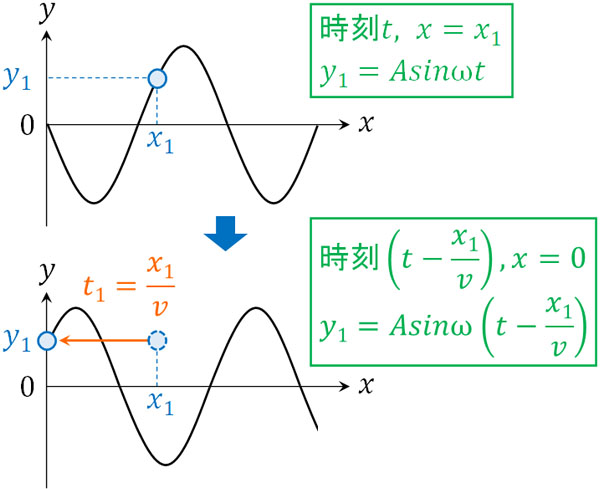
そこで\(x=0\)での変位を表すため、\(y=Asinωt\)の\(t\)を\(t-\displaystyle\frac{x_1}{v}\)に変えましょう。

\(y=Asinω\left(t-\displaystyle\frac{x_1}{v}\right)\)

これが、時刻\(t\)かつ\(x_1\)での\(y\)座標を表す式です。

また\(ωT=2π\)であるため、\(y=Asinωt\)は\(y=Asin\displaystyle\frac{2π}{T}t\)でもあります。そのため、\(t\)を\(t-\displaystyle\frac{x_1}{v}\)に変えると以下のようになります。

\(y=Asin\displaystyle\frac{2π}{T}\left(t-\displaystyle\frac{x_1}{v}\right)\)

\(y=Asin2π\left(\displaystyle\frac{t}{T}-\displaystyle\frac{x_1}{vT}\right)\)

\(y=Asin2π\left(\displaystyle\frac{t}{T}-\displaystyle\frac{x_1}{λ}\right)\)

なお波の式は\(y=Asinωt\)ではなく、\(y=-Asinωt\)になることがあれば、\(y=Acosωt\)になることもあります。この場合であっても、\(t\)を\(t-\displaystyle\frac{x_1}{v}\)に変えることによって、\(x=x_1\)での変位を得られます。

定常波の式は2つの波を足せばいい

それでは、波の式を利用して定常波の式を得るにはどうすればいいのでしょうか。概念は単純であり、2つの波を足しましょう。\(y\)軸方向では、2つの波を足すことによって合成波（定常波）を得られます。

そこで下図について、オレンジの波を\(y_1=Asinω\left(t-\displaystyle\frac{x}{v}\right)\)、緑の波を\(y_2=Asinω\left(t+\displaystyle\frac{x}{v}\right)\)としましょう。

そこで、定常波の式を得るために以下の計算をします。

\(y=y_1+y_2\)

\(=Asinω\left(t-\displaystyle\frac{x}{v}\right)+Asinω\left(t+\displaystyle\frac{x}{v}\right)\)

ここで、以下の三角関数の公式を利用しましょう。

\(sinα+sinβ\)\(=2sin\displaystyle\frac{α+β}{2}cos\displaystyle\frac{α-β}{2}\)

計算すると以下のようになります。

\(y=Asinω\left(t-\displaystyle\frac{x}{v}\right)+Asinω\left(t+\displaystyle\frac{x}{v}\right)\)

\(=2A\)\(sin\displaystyle\frac{ω\left(t-\displaystyle\frac{x}{v}\right)+ω\left(t+\displaystyle\frac{x}{v}\right)}{2}\)\(cos\displaystyle\frac{ω\left(t-\displaystyle\frac{x}{v}\right)-ω\left(t+\displaystyle\frac{x}{v}\right)}{2}\)

\(=2Asin(ωt)cos\left(\displaystyle\frac{ωx}{v}\right)\)

こうして、定常波の式を得ることができました。

定常波の式を利用し、節の場所を計算する

それでは、先ほど得た定常波の式を利用して、節と腹の場所を計算しましょう。節というのは、時間\(t\)に関係なく\(y=0\)になる場所を指します。そこで、以下の式を確認しましょう。

\(y=2Asin(ωt)cos\left(\displaystyle\frac{ωx}{v}\right)\)

この式より、時間\(t\)に関係なく\(y=0\)となるためには、\(cos\displaystyle\frac{ωx}{v}=0\)であればいいとわかります。つまり、\(\displaystyle\frac{ωx}{v}=\displaystyle\frac{π}{2}\)や\(\displaystyle\frac{ωx}{v}=\displaystyle\frac{3π}{2}\)の場合、cosθの値はゼロになります。

数学と同様に記すと、以下のときにcosθの値はゼロになります。

\(\displaystyle\frac{ωx}{v}=\displaystyle\frac{π}{2}+nπ\)

※\(n\)は整数

なお\(ωT=2π\)より、\(ω=\displaystyle\frac{2π}{T}\)です。そのため、以下のように式を変形できます。

\(\displaystyle\frac{ωx}{v}=\displaystyle\frac{π}{2}+nπ\)

\(\displaystyle\frac{2πx}{vT}=\displaystyle\frac{π}{2}+nπ\)

\(\displaystyle\frac{2x}{vT}=\displaystyle\frac{1}{2}+n\)

\(x=\displaystyle\frac{vT(1+2n)}{4}\)

また\(v=fλ\)と\(f=\displaystyle\frac{1}{T}\)より、\(vT=λ\)です。そのため、以下の式を作れます。

\(x=\displaystyle\frac{1+2n}{4}λ\)

こうして、節の位置を得ることができました。

それでは、隣り合う節の間隔を計算してみましょう。言い換えると、\(n\)番目と\(n+1\)番目の節の間隔を計算することになります。この場合、以下のようになります。

\(\displaystyle\frac{1+2(n+1)}{4}λ\)\(-\displaystyle\frac{1+2n}{4}λ\)

\(=\displaystyle\frac{λ}{2}\)

こうして、節の間隔は\(\displaystyle\frac{λ}{2}\)とわかりました。物理で波動を学ぶとき、波長\(λ\)に対して、節の間隔は\(\displaystyle\frac{λ}{2}\)になると学びます。ただ、多くの人は理由を学びません。そこでこのように計算すると、なぜ節の間隔が\(\displaystyle\frac{λ}{2}\)なのか理解できます。

前述の通り、同じ振幅、波長、振動数、速さの波が重なるときに定常波が生成されます。そのため例えば固定端反射で波長が10mの場合、壁に必ず節ができるため、壁から5mおきに節が作られるとわかります。

定常波で腹の間隔は\(\displaystyle\frac{λ}{2}\)になる

次に、腹の間隔を計算しましょう。定常波の式を再び確認します。

\(y=2Asin(ωt)cos\left(\displaystyle\frac{ωx}{v}\right)\)

この式より、時間\(t\)に関係なく\(y\)が最大または最小となるためには、\(cos\displaystyle\frac{ωx}{v}=±1\)であればいいとわかります。つまり、\(\displaystyle\frac{ωx}{v}=0\)や\(\displaystyle\frac{ωx}{v}=π\)の場合、cosθの値は1または-1になります。

以下のときにcosθの値は1または-1になります。

\(\displaystyle\frac{ωx}{v}=nπ\)

※\(n\)は整数

そこで、先ほど解説した方法と同じように計算しましょう。\(ω=\displaystyle\frac{2π}{T}\)より、以下のようになります。

\(\displaystyle\frac{ωx}{v}=nπ\)

\(\displaystyle\frac{2πx}{vT}=nπ\)

\(x=\displaystyle\frac{nvT}{2}\)

また\(vT=λ\)より、以下のようになります。

\(x=\displaystyle\frac{λ}{2}n\)

こうして、定常波で腹となる場所を計算できました。次に、腹と腹の間隔を計算しましょう。

\(\displaystyle\frac{λ}{2}(n+1)-\displaystyle\frac{λ}{2}n\)

\(=\displaystyle\frac{λ}{2}\)