二者択一(結果が2つのみ)のケースは多いです。結果が2つのとき、統計学ではベルヌーイ分布を利用します。ベルヌーイ分布の概念は簡単であり、結果が2つかどうかを確認すればいいです。
結果が2つだけであるため、ベルヌーイ分布の期待値を得る方法は簡単です。一回の試行をするときの確率が期待値になります。ベルヌーイ分布というのは、何度も試行を繰り返すのではなく、一回の試行での分布を指します。
なお、二者択一の確率を利用する分布としては二項分布があります。ベルヌーイ分布と二項分布は何が違うのでしょうか。
概念は簡単であるものの、多くの人にとってベルヌーイ分布という言葉はなじみがありません。そこで、ベルヌーイ分布とは何かを解説していきます。
もくじ
結果が2つだけの試行がベルヌーイ試行
二者択一(結果が2つだけ)の場面は多いです。例えば、以下のケースでは結果が2つです。
- コインを投げるとき:結果は表、または裏
- サイコロを投げるとき:1の目、またはそれ以外
- 製品の品質チェック:合格品、または不良品
結果が2つだけの試行を一回行うとき、得られる分布がベルヌーイ分布です。ベルヌーイ分布では結果が2つだけなので、確率変数は0または1です。
例えばサイコロを投げ、1の目が出たら確率変数0(失敗)、1以外の目が出たら確率変数1(成功)とします。1の目が出る確率は\(\displaystyle\frac{1}{6}\)です。また、1以外の目が出る確率は\(\displaystyle\frac{5}{6}\)です。そのため、以下のようなベルヌーイ分布となります。

通常、統計データを集めるときは複数のサンプルを利用します。ただベルヌーイ分布では、一つの試行の結果を利用します。
ベルヌーイ試行によって得られる分布:ベルヌーイ分布の公式
二者択一の結果を得られるとき、これをベルヌーイ試行といいます。ベルヌーイ分布というのは、ベルヌーイ試行を一回行うことによって得られます。
ベルヌーイ試行によって確率は異なります。例えばコインを投げる場合、表が出る確率は\(\displaystyle\frac{1}{2}\)です。またコインを投げるとき、1の目が出る確率は\(\displaystyle\frac{1}{6}\)です。
ベルヌーイ試行の種類によって確率が違うのは当然です。ただいずれにしても、ベルヌーイ試行では\(x=0\)のときと\(x=1\)のときの2つの確率を得られます。
コインを投げる場合、\(x=0\)(表)の確率は\(\displaystyle\frac{1}{2}\)であり、\(x=1\)(裏)の確率は\(\displaystyle\frac{1}{2}\)です。またサイコロを投げる場合、1の目が出る場合を基準にすると、\(x=0\)(1の目)の確率は\(\displaystyle\frac{1}{6}\)です。また\(x=1\)(1以外の目)の確率は\(\displaystyle\frac{5}{6}\)です。2つの結果について、確率を表すのがベルヌーイ分布です。
なお\(x=1\)となる確率をpとするとき、\(x=0\)の確率は\(1-p\)で計算することができます。すべての確率を足すと1(100%)になるため、これについては理解できると思います。
ベルヌーイ分布で利用される公式(確率質量関数)
前述の通り\(x=1\)(成功)のときの確率が\(p\)の場合、\(x=0\)(失敗)のときの確率は\(1-p\)です。これを難しく記載すると以下のようになります。
- \(P(X=1)=p\)
- \(P(X=0)=1-p\)
またベルヌーイ分布で利用される公式として、以下の確率質量関数があります。
\(P(X=k)=p^k(1-p)^{1-k}\)
※\(k=0,1\)
この公式は何を意味しているのでしょうか。確率質量関数をみると難しい数式のように感じてしまいます。ただ実際には難しくなく、これまで説明してきたことを数式で表しているにすぎません。
前述の通り、ベルヌーイ試行では2つの結果のみ得られます。つまり、ベルヌーイ分布には\(x=0\)または\(x=1\)の2つしかありません。そこで、実際に\(x=0\)または\(x=1\)を確率質量関数に代入してみましょう。
\(P(X=0)=p^0(1-p)^{1-0}=1-p\)
\(P(X=1)=p^1(1-p)^{1-1}=p\)
こうして、\(x=0\)のときの確率は\(1-p\)となり、\(x=1\)のときの確率は\(p\)となります。ベルヌーイ分布の公式は重要ではなく、ここまで解説した単純なことを理解できればそれで充分です。
事象が一回起こる確率がベルヌーイ分布の期待値と分散
それでは、ベルヌーイ分布の期待値\(E(X)\)はどのように計算すればいいのでしょうか。ベルヌーイ分布はベルヌーイ試行を一回行うことによって得られる分布です。そのため、期待値は以下のようになります。
- \(E(X)=p\)
つまり、\(x=1\)(成功)となる確率が期待値\(E(X)\)です。例えば「サイコロを投げて1または3の目が出ると\(x=1\)(成功)」とします。成功確率は\(\displaystyle\frac{1}{3}\)であるため、ベルヌーイ分布での期待値は\(\displaystyle\frac{1}{3}\)です。
一方、分散\(V(X)\)は以下の公式によって得ることができます。
\(V(X)=p(1-p)\)
\(x=0\)の確率と\(x=1\)の確率をかけることによってベルヌーイ分布の分散を計算できます。ただベルヌーイ分布は結果が2つであるため、実際のところ分散を使うことはありません。
ベルヌーイ分布と二項分布との違いは何か
ここまで、ベルヌーイ分布の性質や公式について解説してきました。ただ統計学を学んでいる人の中には「二項分布と何が違うのか?」と疑問に思う人が多いです。
ベルヌーイ分布と二項分布では、両方ともベルヌーイ試行を利用します。つまり、結果が2つのケースを利用して確率分布を得るのです。両方ともベルヌーイ試行を用いるため、違いを理解しにくいです。
そこでベルヌーイ分布と二項分布の違いについて、以下のように理解しましょう。
- ベルヌーイ分布:ベルヌーイ施行を一回行う
- 二項分布:ベルヌーイ試行を何度も行う
結果が2つとなるイベントを一回行う場合、結果は2つです。一方でベルヌーイ試行を何度も行う場合、結果がいくつもあります。
例えばコインを投げる場合、ベルヌーイ分布での結果は2つです(表または裏)。一方で二項分布の場合、コインを8回投げる場合であれば、表が出る確率は出現回数によって8通りあります。
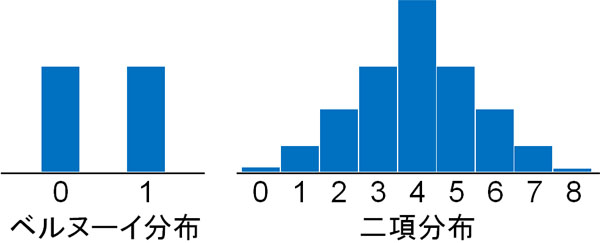
ベルヌーイ試行を何度も行うときの確率分布が二項分布です。ベルヌーイ分布と二項分布の違いというのは、ベルヌーイ試行を一回だけ行うのか、それとも何度も行うのかで判断しましょう。
ベルヌーイ分布と異なり、二項分布は正規分布へ近似できる
結果が2つであるため、当然ながらベルヌーイ分布は正規分布とはなりません。一方で二項分布の場合、グラフの形は正規分布となります。何度も試行を行う場合、グラフの形は正規分布になるという性質があります。これを中心極限定理といいます。
二項分布は正規分布へ近似できるため、正規分布の性質を利用することによって期待値や分散を計算できます。また、確率を計算することによって有意差の判定をすることもできます。
ベルヌーイ試行やベルヌーイ分布を学んでいれば、二項分布の理解に役立ちます。またベルヌーイ分布というのは、二項分布の一部でもあります。
確率の計算方法や期待値・分散を得る公式はベルヌーイ分布と二項分布で異なります。ただベルヌーイ分布と二項分布は似た性質をもつ確率分布であるとわかります。
ベルヌーイ分布の性質や公式を理解する
統計学で学ぶベルヌーイ分布の概念は非常に単純です。結果が2つのベルヌーイ試行について、一回の試行をするときに得られる結果がベルヌーイ分布です。
ベルヌーイ分布の公式(確率質量関数)をみると、難しい数式に思えてしまいます。ただ結果が2つだけであり、\(x=0\)と\(x=1\)の確率がベルヌーイ分布であることを理解すると、内容は難しくないとわかります。
なお、多くの人で混乱するのがベルヌーイ分布と二項分布の違いです。両方ともベルヌーイ試行を利用して確率分布を得ます。ただベルヌーイ分布ではベルヌーイ試行を一回行い、二項分布ではベルヌーイ試行を何度も行います。この違いにより、ベルヌーイ分布と二項分布はグラフの形が大きく異なります。
ここまで解説したことがベルヌーイ分布の内容です。ベルヌーイ分布は結果が2つである分布であることを理解し、ベルヌーイ分布の確率や期待値を計算できるようにしましょう。