相関関係を確認するとき、最も有名な方法がピアソンの相関係数です。2つの要素について、相関関係があるかどうか確認することができます。
一方、複数の要素を含む場合はケンドールの一致係数を利用します。標本に複数の群が含まれている場合、ピアソンの相関係数ではなく、ケンドールの一致係数を利用するのです。
それでは、ケンドールの一致係数を利用してどのように相関関係を確認すればいいのでしょうか。ピアソンの相関係数と比較して何が違うのでしょうか。また、利用する公式や検定の方法はどうなっているのでしょうか。
ケンドールの一致係数はノンパラメトリック法であり、ピアソンの相関係数とは大きく性質が異なります。そこで、ケンドールの一致係数を利用して相関関係を判定する方法を解説していきます。
もくじ
順位を利用して計算する多群でのノンパラメトリック法
2つの要素を比べるのがピアソンの相関係数です。通常、相関関係では複数の要素を比べません。ただ標本に多群を含むことがあり、その場合はピアソンの相関係数ではなく、ケンドールの一致係数を利用します。
2標本ではなく多群の場合、統計学では他の手法を利用するのが一般的です。例えば2標本t検定について、多群では一元配置分散分析や二元配置分散分析を利用します。同様に相関についても、多群ではその他の手法(ケンドールの一致係数)を利用するというわけです。
なお、ケンドールの一致係数はノンパラメトリック法になります。ピアソンの相関係数は母集団が正規分布していることが前提であり、パラメトリック法になります。一方で母集団の正規分布に関係なく利用できるのがパラメトリック法です。
なお、2つの因子について相関関係を確認するノンパラメトリック法にスピアマンの順位相関係数があります。同じノンパラメトリック法ではあるものの、スピアマンの順位相関係数とは異なり、ケンドールの一致係数では多群を取り扱います。
行または列に着目して順位和を計算する
それでは、どのようにケンドールの一致係数を利用して相関関係を求めればいいのでしょうか。多群の検定が可能なノンパラメトリック法としてフリードマン検定があります。ケンドールの一致係数を利用する場合、フリードマン検定と同じように順位和を計算します。
要は、ケンドールの一致係数について、基本的な概念はフリードマン検定と同じです。そのためフリードマン検定について理解している場合、ケンドールの一致係数についても問題なく理解できます。
例として、4つの科目(数学、物理、化学、歴史)のテストを行い、5人の結果が以下の通りだった場面を考えてみましょう。
| Aさん | Bさん | Cさん | Dさん | Eさん | |
| 数学 | 8 | 5 | 7 | 10 | 4 |
| 物理 | 3 | 1 | 3 | 7 | 4 |
| 化学 | 6 | 3 | 2 | 5 | 1 |
| 歴史 | 7 | 6 | 5 | 9 | 2 |
このとき、それぞれの群で相関関係はあるでしょうか。
フリードマン検定では行または列に着目します。行のみ(または列のみ)に着目して検定してもいいし、行と列の両方を検定してもいいます。ケンドールの一致係数についても、行または列のどちらかに着目しましょう。もちろん、行と列の両方の相関関係を調べても問題ありません。
・行に着目する場合
行に着目する場合、今回の例では教科が基準になります。つまり、教科によって難易度に違いがあるかについて、相関関係があるかどうかを確認することができます。
そこで教科について相関関係を確認する場合、列ごとに順位をつけましょう。つまり、それぞれの人でどの教科が最も優れた点数であり、悪い点数だったのか順位をつけるのです。これにより、教科ごとの難易度のランク付けが可能になります。
その後、教科ごとの順位をつけたら、すべての順位を横で足します。これを順位和Rといいます。
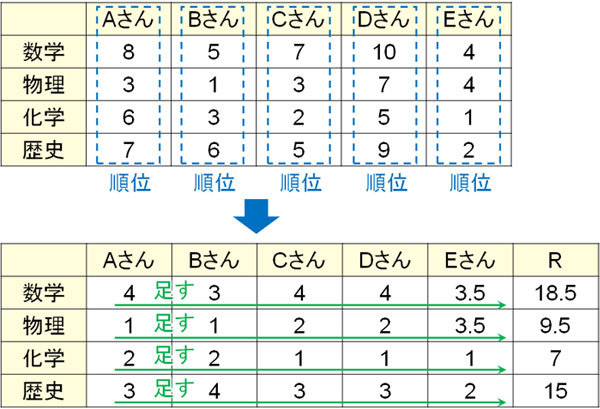
教科ごとに順位を出した後、それぞれの教科で順位を足すことによって順位和Rを計算しましょう。
・列に着目する場合
一方で列に着目することによって相関関係を確認することもできます。列に着目するため、今回の例では「人によって学力に差があるかどうか」を確認することになります。
列に着目する場合、行ごとに順位を出しましょう。これにより、教科ごとの順位を知ることができます。その後、たてで順位和Rを計算することにより、人の学力ごとの順位和を得ることができます。
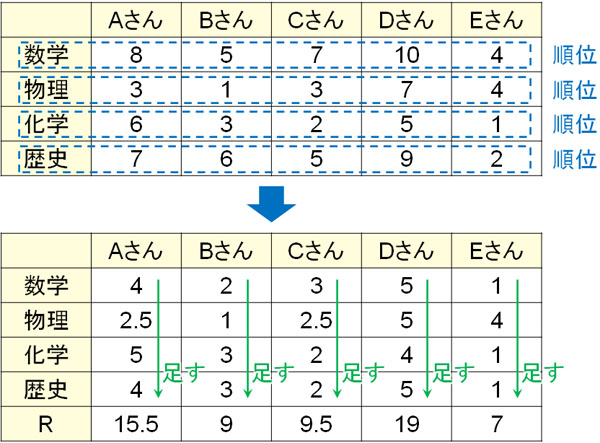
ケンドールの一致係数では順位和Rを利用することで相関を確認します。ここまでの内容や順位和Rの計算方法はフリードマン検定とまったく同じです。
ケンドールの一致係数Wの概念
それでは、ケンドールの一致係数はどのような概念によって相関関係を確認しているのでしょうか。フリードマン検定と同じ方法によって順位和Rを計算するため、検定の概念についてもフリードマン検定と同じです。
相関がある場合、法則性があります。例えば教科ごとに難易度が違う場合、「多くの人で数学の点数は高いものの、物理の点数は低い」などのようになります。その場合、順位和Rの値は異なります。
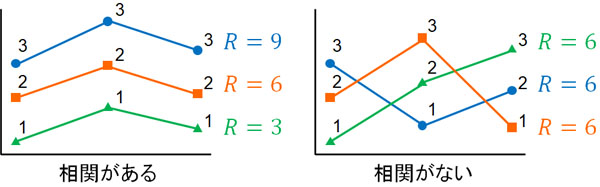
一方で相関がない場合、順位和Rはどれも同じです。順位が一致しないため、順位和Rが同じ値になり、相関なしと判定します。この方法により、相関があるかどうかを判定します。
なお、ケンドールの一致係数はカイ二乗分布に従います。カイ二乗値が大きい場合、相関関係があると判断します。
順位を付けた後、足すことで順位和Rと偏差平方和Sを求める
それでは、実際にケンドールの一致係数を利用して多群の相関関係を確認してみましょう。まず、順位をつけて足すことによって順位和Rを求めましょう。
先ほどの例であれば、行(教科ごとの難易度)に着目すると以下のように順位和Rを求めることができます。
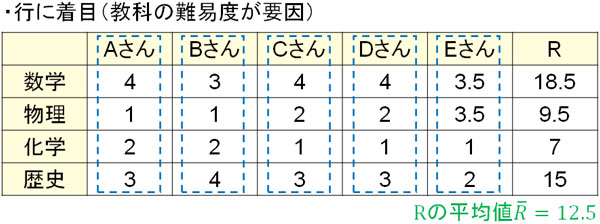
このとき、帰無仮説と対立仮説は以下の通りです。
- 帰無仮説:教科の難易度の相関はない
- 対立仮説:教科の難易度に相関がある
計算すると、Rの平均値は12.5です。順位和とRの平均値を出せば、順位和Rの偏差平方和Sを出すことができます。偏差平方和Sを得る公式は以下になります。
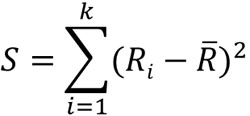
そこで、公式に当てはめることで偏差平方和Sを計算しましょう。Rの平均値は12.5であるため、以下のようになります。
\(S=(18.5-12.5)^2\)\(+(9.5-12.5)^2\)\(+(7-12.5)^2\)\(+(15-12.5)^2=81.5\)
こうして、偏差平方和Sは81.5であるとわかりました。相関がない場合、それぞれの群の順位和RはRの平均値と同じになるため、偏差平方和Sの値はゼロです。一方で相関(法則性)がある場合、それぞれの群の順位和RとRの平均値は異なるため、偏差平方和Sの値は大きくなります。
群数とデータ数の関係を理解する
次にケンドールの一致係数Wとカイ二乗値χ2を求めましょう。その前に重要なポイントとして、群数\(k\)とデータ数\(n\)を見極めることがあります。行に着目するのか、列に着目するのかによって群数とデータ数は異なります。
行に着目する場合、行の数が群数になり、列の数がデータ数になります。一方で列に着目する場合、列の数が群数になり、行の数がデータ数になります。
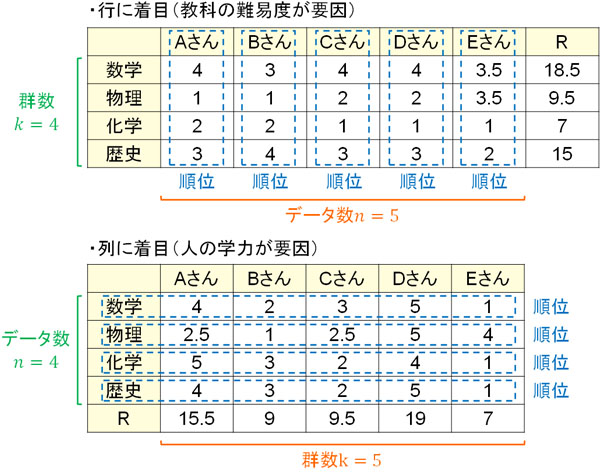
今回は行(教科の難易度)に着目するため、群数\(k\)は4であり、データ数\(n\)は5です。
ケンドールの一致係数Wとカイ二乗値を得た後、検定によって相関関係を判定する
偏差平方和Sや群数\(k\)、データ数\(n\)がわかれば、ケンドールの一致係数Wを計算できます。ケンドールの一致係数Wを得る公式は以下になります。
- \(W=\displaystyle\frac{12S}{n^2(k^3-k)}\)
そこで、公式に数字を代入しましょう。
\(W=\displaystyle\frac{12×81.5}{5^2×(4^3-4)}=0.652\)
こうして、ケンドールの一致係数Wは0.652とわかりました。なお、ケンドールの一致係数Wの範囲は必ず\(0≦W≦1\)になります。
次にカイ二乗値を計算しましょう。ケンドールの一致係数Wを利用する場合、カイ二乗値χ2は以下のようになります。
- \(χ^2=n(k-1)W\)
そこで公式に数字を代入しましょう。
\(χ^2=5×(4-1)×0.652=9.78\)
カイ二乗値は9.78であり、この数字と有意水準を比較します。
なお有意水準とp値を比較するとき、ケンドールの一致係数では2パターンあります。それぞれ以下のようになります。
【群数\(k\)が4以下の場合】
フリードマン検定表を利用して判定しましょう。
【群数\(k\)が5以上の場合】
計算によって得たカイ二乗値χ2について、近似的に自由度\(n-1\)のカイ二乗分布とみますことができます。そこでカイ二乗分布を利用して判定しましょう。
・判定を行う
先ほどの例の場合、群数は4です。そこでカイ二乗分布ではなく、フリードマン検定表を利用して判定します。統計学の教科書を利用すると、群数\(k\)が4でデータ数\(n\)が5のとき、有意水準0.05(5%)での値は7.80です。
つまり7.80よりも数字が大きい場合、5%以下で起こる稀なイベントが発生していると判断できます。そこで計算したカイ二乗値を確認すると9.78です。7.80よりも値は大きいため、帰無仮説を棄却して対立仮説を採用しましょう。つまり、教科の難易度には相関がある(一貫性がある)と判断できます。
多群の相関関係を確認できるケンドールの一致係数
フリードマン検定を理解している場合、ケンドールの一致係数を学ぶのは難しくありません。検定の概念や順位和Rの計算方法は同じだからです。利用する公式が違うだけであり、フリードマン検定やケンドールの一致係数は内容が同じです。
フリードマン検定は多群の差を確認するノンパラメトリック法です。一方でケンドールの一致係数は相関を確認する方法です。
また相関を確認する方法の中でも、ピアソンの相関係数やスピアマンの順位相関係数とは異なり、多群の相関を確認できます。相関がある場合、各群の順位和Rと順位和の平均値は異なります。そのため相関がある場合、ケンドールの一致係数Wは1に近づきます。
このようにして、ノンパラメトリック法によって多群の相関関係を確認するのがケンドールの一致係数です。多群の相関関係を知りたい場合はケンドールの一致係数を利用しましょう。






