ベイズ推定をするとき、必ず利用するのが事前分布と事後分布です。このとき、事前分布と事後分布の種類が一致していると計算が簡単であり、非常に都合がよいです。
そうしたとき、ベイズ推定での計算を簡単にしてくれるのが共役事前分布です。連続確率分布を取り扱うとき、共役事前分布を利用すると便利なのです。共役事前分布を使えば、事前分布と事後分布の種類が同じになるという性質があります。
それでは、共役事前分布とは何なのでしょうか。また、具体的にどのような種類があるのでしょうか。
ベイズ統計学を利用して未来の予測をするとき、共役事前分布を利用しましょう。これにより、難しい計算なしに将来の確率を予測できるようになります。
もくじ
ベイズ推定では尤度を利用し、事後分布を得る
共役事前分布を理解するためには、ベイズ定理の公式を復習する必要があります。ベイズ統計学で事後分布を得るとき、事前分布と尤度(データを得られる確率)を利用します。以下がベイズ推定で利用される公式です。
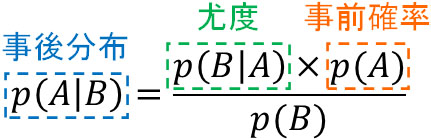
何かイベントが発生することによって確率が変化します。事前分布から事後分布へと変化するのです。
例えばトランプのカードを引くとき、絵札を引くと正解とします。「カードが絵札かどうか\(P(A)\)」「カードが3の倍数かどうか\(P(B)\)」を利用して4つに分けると以下のようになります。
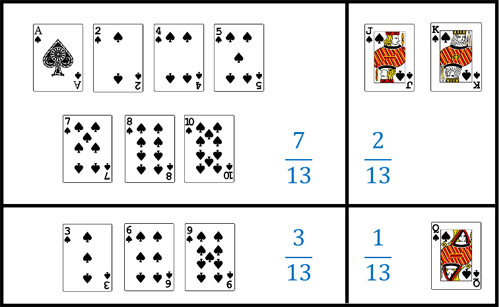
カードが絵札である確率は\(\displaystyle\frac{3}{13}\)です。ただあなたがカードを引いた後、司会者は「あなたが引いたカードは3の倍数です」と教えてくれます。
こうして条件が変化し、確率は以下のように「カードが3の倍数のうち、絵札を引く確率\(P(A|B)\)」である\(\displaystyle\frac{1}{4}\)へ変化します。イベント発生後に得られるこの確率が事後確率です。
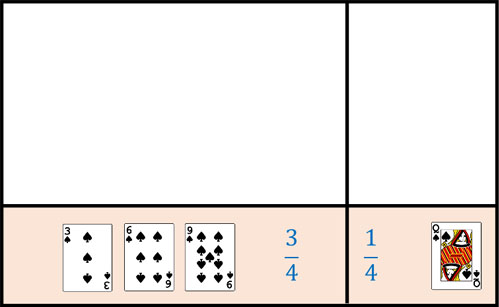
事前確率(絵札を引く確率\(P(A)\))は\(\displaystyle\frac{3}{13}\)です。また、尤度(絵札のうち、3の倍数を引く確率\(P(B|A)\))は\(\displaystyle\frac{1}{3}\)です。3の倍数を引く確率\(P(B)\)は\(\displaystyle\frac{4}{13}\)です。
そこで先ほどの公式に当てはめると以下のようになります。
\(\displaystyle\frac{\displaystyle\frac{1}{3}×\displaystyle\frac{3}{13}}{\displaystyle\frac{4}{13}}=\displaystyle\frac{1}{4}\)
こうして、ベイズ定理の公式を利用しても事後確率を得ることができます。共役事前分布を理解するためには、こうしたベイズ推定の内容を把握しておく必要があります。
なおわかりやすくするため、トランプを利用し、明確な確率(特定の値)を利用して解説しました。一方で確率密度関数を計算する場合、特定の値ではなく\(x\)などの文字が入った数式を利用して計算することになります。これにより、事前分布が事後分布へと変化するのです。
いずれにしても、ベイズ推定では何かしらのイベントが発生することによって事前分布から事後分布へと変化します。
事前分布と事後分布が同じになる共役事前分布とは
それでは、先ほどのトランプの例を考えてみましょう。事前確率から事後確率へ変化するとき、特に違和感はなかったと思います。この理由として、事前確率と事後確率で分布が同じだからです。
事前分布では、1~13のすべてのカードについて確率は\(\displaystyle\frac{1}{13}\)です。すべての確率が同じ場合、一様分布といいます。
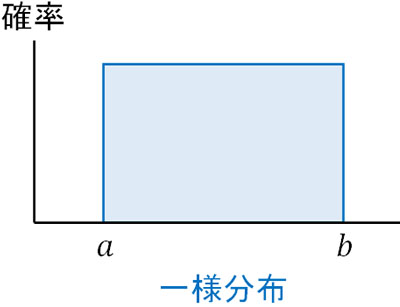
一方、事後分布の確率はどうでしょうか。トランプで3の倍数は3、6、9、12です。これらのカードのうち、引く確率はそれぞれ\(\displaystyle\frac{1}{4}\)です。つまり、先ほどと同じ一様分布です。
ベイズ推定では必ず尤度をかけます。このとき事前分布を正しく選ぶと、事前分布と事後分布が同じになります。この性質をもつ事前分布を共役事前分布といいます。
一様分布はベータ分布の一つであり、ベータ分布の特殊なケースが一様分布です。また、ベータ分布は共役事前分布の一つです。ベータ分布(一様分布)は共役事前分布であるため、事後分布もベータ分布となったのです。
分布が違うと前提条件が異なる
ベイズ推定をするとき、事前分布と事後分布が異なるとどうなるのでしょうか。例えば尤度をかけることによって、以下のようにまったく異なる分布を得られるケースはどうでしょうか。
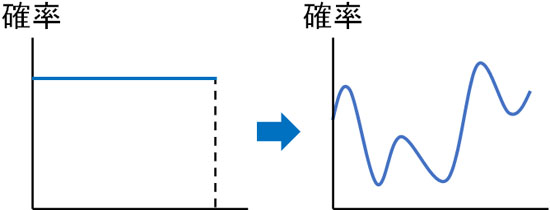
この場合、事前分布に対して事後分布が何を意味しているのか理解するのが難しいです。事後分布の期待値(平均)や分散を得たとしても、事前分布との比較ができません。つまりベイズ推定を利用しても、将来の予測が正確ではありません。また、計算が大変です。
事前分布と事後分布が同じであることは重要です。分布が同じ場合、変化前と変化後を比較することによって、確率分布がどのように変化したのか把握できます。例えば事後分布の期待値を得ることができれば、難しい計算なしに、イベント発生による期待値(平均)の変化がわかります。
ベイズ推定で共役事前分布を多くの人が意識するのは、事前分布と事後分布を一致させることによるメリットが多いからなのです。
具体的な共役事前分布の例:指数型分布族との関係
それでは、具体的にどのような共役事前分布があるのでしょうか。先ほど提示した例は一様分布(特殊なベータ分布)です。当然、共役事前分布にはベータ分布以外にも存在します。
共役事前分布としては以下が知られています。
| 事前分布 | 尤度関数(分布) | 事後分布 |
| ベータ分布 | ベルヌーイ分布 | ベータ分布 |
| ベータ分布 | 二項分布 | ベータ分布 |
| 正規分布 | 正規分布 | 正規分布 |
| ガンマ分布 | ポアソン分布 | ガンマ分布 |
| ディリクレ分布 | 多項分布 | ディリクレ分布 |
代表的な共役事前分布を掲載しましたが、ほかにも共役事前分布は存在します。
なお、一般的に尤度関数が指数型分布族の場合、共役事前分布が存在します。指数型分布族には正規分布やベータ分布、ポアソン分布、指数分布、ガンマ分布、カイ二乗分布、幾何分布など、私たちが一般的に利用する分布(特異モデルの分布ではないケース)が含まれます。
共役事前分布を利用してベイズ推定を行う
計算の前後で分布が違うと不都合なことが起こります。計算が大変になりますし、事後分布を用いた未来の予想が正確でなくなってしまう恐れがあります。
そこで、ベイズ推定を行うときは事前分布と事後分布を同じにさせましょう。これを可能にするのが共役事前分布です。正しく事前分布を選べば、ベイズ推定をすることによって事前分布と事後分布が一致します。
なぜ共役事前分布が重要かというと、共役事前分布を利用することによって事後分布の計算が簡単になり、ベイズ推定を利用しての将来の予測をしやすくなるからです。
統計処理をするとき、イベント発生の前後によって分布が変化すると不都合な事態に陥ります。そこで分布を一致させるため、共役事前分布を利用しましょう。