少数のサンプルを利用することによって、母集団の平均値を予想する方法が推測統計です。推測統計学で最もわかりやすいのは点推定です。例えば平均値や中央値などを求めるのは点推定です。
一方で特定の区間を利用して予想するのが区間推定です。点推定に比べると、区間推定は少し概念が難しくなります。ただ統計学では、非常に多くの場面で区間推定を利用します。そのため、区間推定を理解しなければいけません。
区間推定で頻繁に利用される概念が95%信頼区間と99%信頼区間です。統計処理するとき、95%や99%の確率から逸脱している場合、「何か特殊なことが起こっている」と考えるのです。
区間推定は学術研究や品質管理、マーケティングなど、あらゆる場面で利用されます。ここでは、区間推定や信頼区間の内容を解説していきます。
もくじ
点推定と違い、区間推定では一定区間で判断する
統計データを集めるとき、最も良い方法は全数調査をすることです。全体のデータ(母集団)を集めることによって、真の値がわかります。
ただ多くの場合、全データを集めるのは困難です。例えば国民の成人男性の平均体重はいくらでしょうか。これを厳密に調べるのは不可能であり、一つの国に住んでいる男性全員の体重を調べることはできません。そもそも、体重測定に協力してくれない人は多いです。
そこで例えばランダムに選んだ100人の体重を測定します。標本として一部の人のデータを利用することで、標本の平均値を得ることができます。これにより、母集団の平均値を予想することができます。これが推測統計です。
今回の場合、標本の平均値が65kgだったとします。その場合、国民の成人男性の平均体重は65kgと推定できます。また、一つの値によって母集団の性質を推定するのが点推定です。
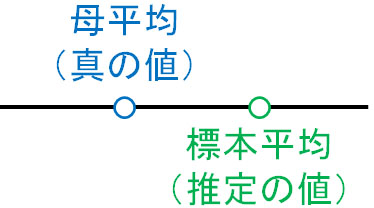
母平均(真の値)がどこになるのか知ることはできません。ただ標本平均を利用することによって、一つの点によって母平均を推定するのです。
一方で点ではなく、特定の区間を利用して真の値の場所を推測するケースが頻繁にあります。これを区間推定といいます。先ほどの例を利用する場合、区間推定では以下のようになります。
- 成人男性の体重は95%の確率で61~71kg
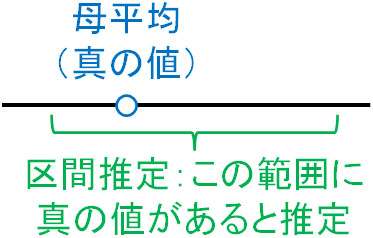
このように、確率分布を利用することによって範囲を出します。真の値から逸脱する例はあるものの、多くの場合で区間推定によって得た範囲内に真の値が収まるというわけです。
標準偏差・標準誤差を利用し、95%信頼区間や99%信頼区間を得る
なお、区間推定では95%や99%が頻繁に利用されます。そこで区間推定を利用する場合、95%信頼区間または99%信頼区間を利用しましょう。前述の通り、確率分布を利用するのが区間推定です。
確率分布を利用することになるため、区間推定では正規分布や二項分布を利用することになります。データが正規分布するとき、平均値を\(μ\)、標準偏差を\(σ\)とすると、すべての正規分布について以下の関係が成り立ちます。
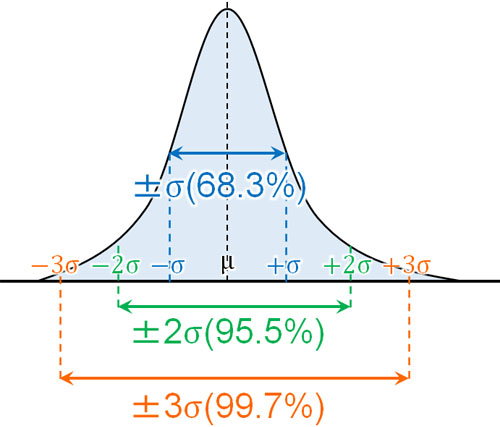
つまり平均値\(μ\)を基準にして、標準偏差の2倍(\(2σ\))の距離にある範囲に全データの95.5%が含まれています。また標準偏差の3倍(\(3σ\))の距離にある範囲に全データの99.7%が含まれています。
なお、95.5%や99.7%という数字を見たとき、95%や99%に値が近いと思わないでしょうか。つまり平均値\(μ\)と標準偏差\(σ\)を利用することによって、95%信頼区間や99%信頼区間を計算できることがわかります。
信頼区間の意味を理解する
それでは、信頼区間とは何を意味しているのでしょうか。95%信頼区間や99%信頼区間を計算する前に、まず信頼区間の意味を理解しましょう。95%信頼区間について、多くの人は以下のように勘違いします。
- 真の値が95%の確率で信頼区間の中に存在する。
例えば先ほど、成人男性の平均体重を測定する場面について、「成人男性の体重は95%の確率で61~71kg」と記しました。わかりやすく説明するためこのように記しましたが、正確にいうとこの表現は間違いです。
そうではなく、95%信頼区間は以下のように考えます。
- 真の値は固定されており、標本データを集めて100回測定すると、95%の確率で真の値を含む。
つまり100回測定する場合、5回は真の値を含まないことがあるのです。図にすると以下のようになります。
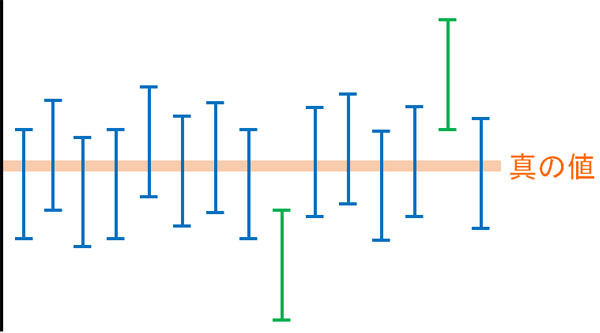
当然ですが、真の値は固定されており、動くことはありません。動くのは標本データのほうです。使用するデータによって95%信頼区間が動き、場合によっては真の値から大きくズレることがあるのです。
95%信頼区間や99%信頼区間で重要な標準誤差
ここまでのことを理解して、95%信頼区間や99%信頼区間を求めましょう。95.5%を95%へ変えるとき、また99.7%を99%へ変えるとき、標準誤差を利用します。標準誤差というのは、標準偏差の親せきと理解しましょう。
標準偏差は母集団のデータのばらつきを表します。一方で標準誤差では、標本のサンプル数を考慮したデータのばらつきを表します。
例えば成人男性の平均体重を得るとき、10人の体重を調べるのと、1000人の体重を調べるのでは、1000人を調べるほうがデータの信頼性は高いです。そこで標準偏差に対して、データの信頼性を加えた指標が標準誤差です。
標準偏差\(σ\)と標準誤差SEは以下の公式で表されます。
- \(SE=\displaystyle\frac{σ}{\sqrt{n}}\)
サンプル数\(n\)の値が大きくなるほど、標準誤差SEの値は小さくなります。サンプル数が多いほど信頼できるデータになるため、それに伴ってSEの値も小さくなるのです。
また、標準誤差は平均値のばらつきを表します。標本のサンプル数が多いほど、平均値のばらつきは小さくなるはずです。
統計では、データが多いほど真の値に収束するという性質があります。これを中心極限定理といいます。いずれにしてもサンプル数が多いと、標本の平均値のばらつき(標準誤差)は小さくなることを理解しましょう。
標準偏差と標準誤差の違いとしては、以下のようになります。
- 標準偏差:サンプル一つ一つのばらつき
- 標準誤差:データの平均値のばらつき
なお先ほど、「平均値\(±2σ\)(標準偏差)に全データの95.5%が含まれている」「平均値\(±3σ\)(標準偏差)に全データの99.7%が含まれている」ことを説明しました。
同じように、標準誤差では以下のように考えます。
- 平均値\(±2SE\)(標準誤差)に95.5%の平均値が含まれている
- 平均値\(±3SE\)(標準誤差)に99.7%の平均値が含まれている
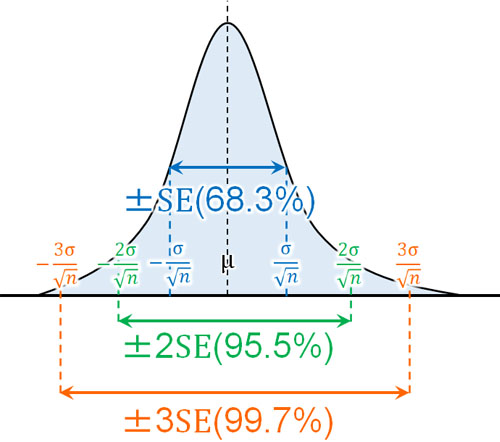
ただ2倍すると95.5%になってしまいます。そこで95%にするため、2倍ではなく1.96倍をかけましょう。また3倍すると99.7%になってしまいます。そこで99%にするため、3倍ではなく2.58倍をかけましょう。
そのため95%信頼区間や99%信頼区間を得る公式は以下のようになります。
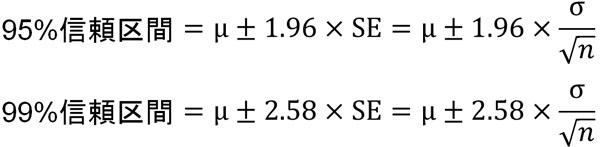
要は上の式のように、標準誤差に1.96をかけることによって95%信頼区間を得られます。また標準誤差に2.58をかけることによって99%信頼区間を得られます。
なお標本平均の標準偏差というのは、母集団の標準偏差に比べて、正規分布の左右が\(\displaystyle\frac{1}{\sqrt{n}}\)小さくなることが知られています。
・母標準偏差ではなく、標準誤差(標本標準偏差)を利用する理由
母集団はすべてのデータを含みます。その中から少数のサンプルを取り出すとき、母平均に近いデータを選ぶことになる可能性が高いです。そのため標本標準偏差というのは、母標準偏差(母集団の標準偏差)に比べて正規分布の幅が狭くなります。
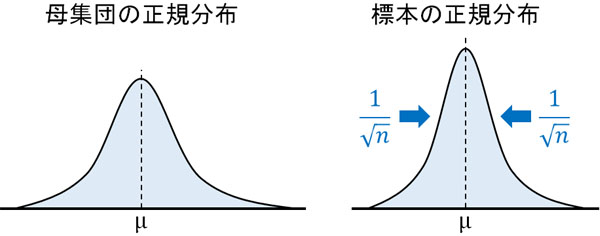
95%信頼区間というのは、標本(少数のサンプル)を利用して計算します。母集団は不明であるため、母標準偏差はわかりません。そのため母標準偏差\(σ\)ではなく、標本標準偏差(標準誤差)である\(\displaystyle\frac{σ}{\sqrt{n}}\)を利用する必要があります。
つまり標準誤差というのは、「母集団からサンプルとして複数のデータを取り出し、調べるときの標準偏差」といえます。母標準偏差ではなく、標準誤差を利用するのは、標本の標準偏差を利用して95%信頼区間(または99%信頼区間)を出すからなのです。
信頼区間を用いた母平均の推定
それでは、実際に95%信頼区間を計算してみましょう。以下の問題の答えは何でしょうか。
- ある製品についてランダムに100個を抽出して調べると、製品の寿命は平均1000時間でした。製品の寿命は正規分布し、標準偏差が200の場合、95%信頼区間を求めましょう。
これまで説明したことを理解しているのであれば、95%信頼区間の計算をすることができます。公式に当てはめることによって95%信頼区間を求めましょう。
\(1000±1.96×\displaystyle\frac{200}{\sqrt{100}}=960.8,1039.2\)
- \(μ=1000\)
- \(σ=200\)
- \(n=100\)
こうして、95%信頼区間は[960.8, 1039.2]であるとわかります。正規分布と標準偏差の関係を理解しており、標準誤差の概念を学べば、信頼区間の計算を行えるようになります。
今回のような計算をしても、母平均(真の値)がどこにあるのかわかりません。ただランダムサンプリング(無作為抽出)を100回して、そのうち95回は母平均が980~1200時間の中に含まれます。そのため、ひとまず母平均は960.8~1039.2時間の間にあるのではと推測できます。
区間推定をするとき、どれだけ信頼できるのかを表すのが95%信頼区間や99%信頼区間と理解しましょう。
母比率の推定:標本比率を用いて計算する
なお先ほど、母平均について95%信頼区間を用いて推測しました。このとき当然ながら、母平均以外の項目についても信頼区間を利用することができます。その一つが母比率です。
ある特定の性質を記す要素について、その割合を母比率といいます。例えば全校生徒のうち、30%が自転車で学校へ通っている場合、自転車を利用している生徒の母比率は30%です。
ただ母集団を調べるのは大変なので、標本比率を調べることがよくあります。標本として少数のサンプルを集め、標本の標準偏差を調べることによって区間推定するのです。このときサンプル数を\(n\)、そのうち特定の性質をもつ要素の数を\(X\)とすると、標本比率\(R\)は以下のように表されます。
- \(R=\displaystyle\frac{X}{n}\)
例えば標本のサンプル人数が100であり、そのうち45人が自転車で学校に通っている場合、標本比率は0.45です。そのため、この公式については容易に理解できると思います。
先ほど母平均を計算するとき、平均値のばらつき(標準誤差)を利用することによって95%信頼区間を求めました。同じように考えて、標本比率のばらつきを利用することによって信頼区間を計算できるというわけです。
式の証明は省きますが、標本比率\(R\)のばらつきは以下の式によって表されます。
- \(\sqrt{\displaystyle\frac{R(1-R)}{n}}\)
そこで母比率の95%信頼区間や99%信頼区間を求める場合、以下の公式になります。
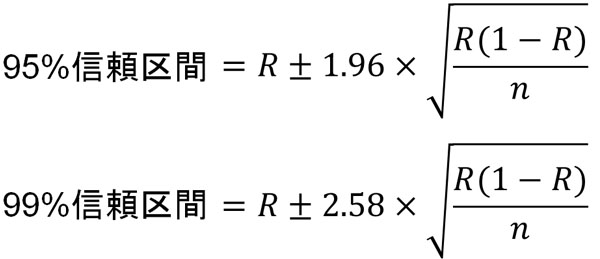
公式は少し異なるものの、考え方はこれまでと同じです。標本比率\(R\)を用いて信頼区間を求めるため、平均値\(μ\)の代わりとして標本比率\(R\)を利用しましょう。さらには標本比率の標準偏差を利用して信頼区間を得るのです。
得た結果を判断するため、95%信頼区間や99%信頼区間を利用する
なお区間推定というのは、標本を利用することによって得られた結果が特別な意味をもつのかどうかを判断するために利用するケースが多いです。異常値が出たとしても、それが本当に異常なのかどうか客観的に判断するために区間推定を活用するのです。
例えば薬の効果を調べるとき、偽薬の投与群と薬Aの投与群を比較するとき、薬Aに効果があると提示するときは区間推定を利用します。より詳しくいうと、95%信頼区間または99%信頼区間を活用します。
もし偽薬の群と薬Aの群に明らかな効果の違い(データの違い)がある場合、統計処理することによって95%(または99%)の信頼度で「2つの群に違いがある」と判定するのです。
母集団がわからない以上、「両者には必ず違いがある」と断言することはできません。ただ100回のうち95回(または99回)の頻度で違いがあるといえる場合、両者に違いがあると考えて問題ないはずです。
95%信頼区間や標準誤差、母平均・母比率の概念を理解する
推定統計学は頻繁に利用され、仕事内容によっては95%信頼区間や99%信頼区間を毎日のように使うことになります。それだけ重要であり、利用頻度の高い概念が区間推定です。
ただ初めて区間推定について学ぶとき、概念を理解するのが難しいです。点推定とは違い、区間推定では特定の範囲を利用して判断することになります。そこで95%信頼区間や99%信頼区間の意味を理解しましょう。
また95%信頼区間(または99%信頼区間)を利用し、母平均・母比率を推定できるようにしましょう。特に母平均の推定は利用頻度が高く、計算することによってデータに差があるかどうかを確認できます。
統計学で重要な内容が区間推定です。そこで95%信頼区間や99%信頼区間が何を意味しているのか学び、計算できるようにしましょう。