最も基本的な確率分布に一様分布があります。コインやサイコロを投げるとき、一様分布になります。すべての確率が同じ場合は一様分布です。
一様分布には離散一様分布と連続一様分布の2種類があります。両者は似ているものの、異なる分布です。また、期待値や分散を得る公式も異なります。
一様分布は多くの場面で利用されます。発生確率が常に同じとなるイベントはたくさんあるからです。そこで離散一様分布と連続一様分布について、期待値(平均)や分散の計算、累積分布関数での違いを理解しましょう。
統計学で重要な分野の一つが一様分布です。そこで、一様分布の特徴や公式の意味を解説していきます。
もくじ
一様分布とは何か:最も基本的な分布の一つ
一定区間について、すべての確率が同じ場合は一様分布と呼ばれます。例えばコインを投げるとき、表と裏の出る確率はそれぞれ\(\displaystyle\frac{1}{2}\)です。
またサイコロを投げる場合、出る目の確率はすべて\(\displaystyle\frac{1}{6}\)になります。以下はサイコロを投げるとき、出る目の確率です。

このような確率分布を一様分布といいます。一様分布の例としては以下があります。
- コインやサイコロを投げる
- 一年での月ごと死亡率
- 毎日の不良品の発生割合
例えば、生命保険会社は保険商品を設計するときに一様分布を利用します。大災害が発生しない限り、通常は特定の月に死亡率が大きくなることはありません。そこで過去の統計結果と一様分布を利用して保険商品を作成するのです。これは一つの例ではありますが、確率が常に一定であるケースは多いです。
一様分布には離散型確率分布と連続型確率分布がある
ただ一様分布には離散一様分布(離散型確率分布)と連続一様分布(連続型確率分布)があります。そこで、離散一様分布と連続一様分布の違いを理解しましょう。
離散型確率分布の場合、特定の点にて明確な確率を述べることができます。例えばサイコロを投げるとき、1の目が出る確率は\(\displaystyle\frac{1}{6}\)です。1の目が出る場合について明確な確率を述べることができるため、サイコロを利用する場合は離散型確率分布になります。
一方で連続型確率分布の場合、特定の点を指し示すことができません。例えば長さや重さが連続型確率分布に該当します。
例えば身長170cmの人について、ピッタリ170.0000cmの人はほとんどいません。身長は170.0402cmかもしれませんし、169.9984cmかもしれません。コインやサイコロのように、特定の点を決めることができないのです。
そのため連続型確率分布の場合、確率分布は連続している線でつながります。グラフにすると、離散一様分布と連続一様分布は以下のようになります。
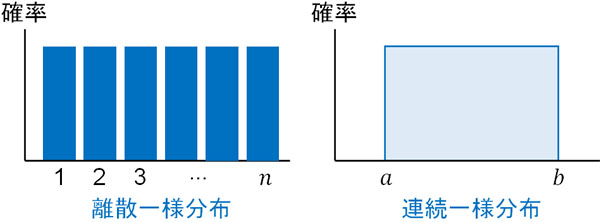
コインやサイコロのように、不連続な値を取る場合は離散一様分布です。一方で長さや重さのように、細かい値を設定することができ、グラフが連続してつながる場合は連続一様分布です。
離散一様分布の確率質量関数
それでは、離散一様分布の確率を得るにはどのようにすればいいのでしょうか。考え方はシンプルであり、1を全体の数\(n\)で割りましょう。
すべての確率を足すと1(100%)になります。また一様分布では、すべての確率が同じです。そのため全体の数でわると確率を得られるのは当然です。例えばコインを投げる場合、表と裏の2種類です。全体の数は2つなので、コインを投げるときの確率は\(\displaystyle\frac{1}{2}\)です。
またサイコロの場合、6つの数字があります。つまり、全体の数は6です。そのためサイコロを投げる場合、それぞれ出る目の確率は\(\displaystyle\frac{1}{6}\)です。
離散一様分布では、確率質量関数\(f(x)\)を以下の公式で表します。
- \(f(x)=\displaystyle\frac{1}{n}\)
確率質量関数とは、離散一様分布で確率を得るための公式を指します。離散一様分布での確率質量関数\(f(x)\)というのは、1を全体の数\(n\)で割ることで得られます。ただ、この公式に特別な意味はなく、当たり前のことを数式で表しているにすぎません。
期待値を計算する公式
それでは、離散一様分布で期待値\(E(X)\)を得る公式には何があるのでしょうか。離散一様分布で期待値を計算するとき、以下の公式を利用します。
- \(E(X)=\displaystyle\frac{n+1}{2}\)
なぜ、この公式によって離散一様分布の期待値を計算できるのでしょうか。期待値(平均)というのは、それぞれの確率変数と確率を計算することによって得られます。例えばサイコロの場合、以下のように計算することで期待値3.5を得ることができます。
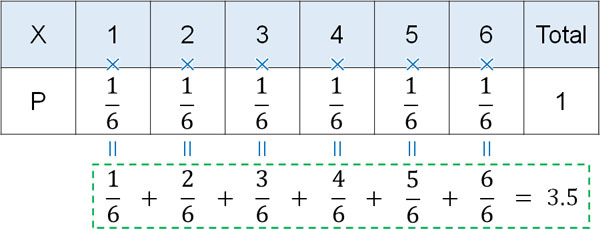
そのため、離散一様分布の期待値は確率Pを利用して以下のように計算できます。
\(E(X)=x_1P+x_2P+…x_nP\)
\(=\displaystyle\sum_{k=1}^{n}{kP}\)
前述の通り、離散一様分布では\(P=\displaystyle\frac{1}{n}\)です。そのため、以下のように期待値(平均)の公式を導くことができます。
\(\displaystyle\sum_{k=1}^{n}{kP}\)
\(\displaystyle\sum_{k=1}^{n}{k×\displaystyle\frac{1}{n}}\)
\(=\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}{k}\)
\(=\displaystyle\frac{1}{n}×\displaystyle\frac{n(n+1)}{2}\)
\(=\displaystyle\frac{n+1}{2}\)
\(\displaystyle\sum_{k=1}^{n}{k}\)については、等差数列の公式を利用しましょう。こうして、\(E(X)=\displaystyle\frac{n+1}{2}\)であるとわかります。
分散の公式を導き出す過程
次に離散一様分布の分散\(V(X)\)を計算しましょう。離散一様分布での分散を得る公式は以下になります。
\(V(X)=\displaystyle\frac{n^2-1}{12}\)
それでは、この公式を導き出しましょう。分散を得るためには、期待値(平均)を利用して、以下の公式を利用することで得られることは既に学んでいると思います。
- \(V(X)=E(X^2)-E(X)^2\)
この公式へ代入することによって分散の公式を得ましょう。\(E(X^2)\)というは、確率変数\(X\)を二乗した後、期待値を計算することを意味します。そのため、以下のようになります。
\(E(X^2)=(x_1)^2P+(x_2)^2P+…(x_n)^2P\)
\(=\displaystyle\sum_{k=1}^{n}{k^2P}\)
\(=\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}{k^2}\)
また、\(E(X)^2\)は期待値の二乗を意味します。そのため、以下のような計算になります。
\(V(X)=E(X^2)-E(X)^2\)
\(=\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}{k^2}\)\(-\left(\displaystyle\frac{n+1}{2}\right)^2\)
\(=\displaystyle\frac{(n+1)(2n+1)}{6}\)\(-\left(\displaystyle\frac{n+1}{2}\right)^2\)
\(=\displaystyle\frac{n^2-1}{12}\)
こうして、高校数学の知識を利用することによって離散一様分布で分散を得る公式を得ることができました。なお標準偏差を出したい場合、平方根を利用して計算しましょう。
累積分布関数のグラフの形を理解する
次に累積分布関数でのグラフの形を学びましょう。すべての確率を足していくのが累積分布関数です。すべての確率を足すため、最終的に確率は必ず1(100%)になります。
例えばサイコロを投げる場合、出る目の確率はそれぞれ\(\displaystyle\frac{1}{6}\)です。そのため累積分布関数では、\(\displaystyle\frac{1}{6}\)ずつ値が大きくなります。
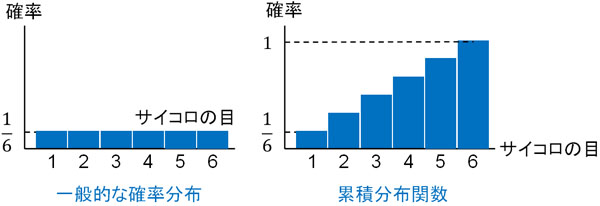
また前述の通り、サイコロを投げるときは離散一様分布です。そのため離散一様分布での累積分布関数では、一定割合で値が増えていくと理解しましょう。
なお、離散一様分布での確率Pは\(\displaystyle\frac{1}{n}\)であると解説しました。そのため累積分布関数では、\(\displaystyle\frac{1}{n}\)ずつ値が増えていきます。
連続一様分布での確率密度関数は面積を利用する
離散一様分布を理解した後、連続一様分布を学びましょう。連続一様分布で確率(確率密度関数\(f(x)\))を得る公式は以下のようになります。
\(f(x)=\displaystyle\frac{1}{b-a}\)\((a≤x≤b)\)
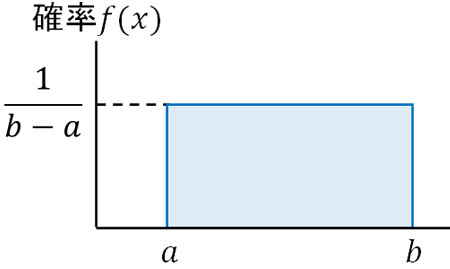
\(a≤x≤b\)のとき、連続一様分布での確率は必ず\(f(x)\)\(=\displaystyle\frac{1}{b-a}\)になります。そのため、たて軸(確率)の値は\(f(x)\)\(=\displaystyle\frac{1}{b-a}\)です。
なぜ\(f(x)\)\(=\displaystyle\frac{1}{b-a}\)となるのかについて、すべての確率を足すと1(100%)になるからです。つまり、面積(たて×横)は1になる必要があります。グラフの横の長さは\(b-a\)です。そこでたての長さを\(x\)とすると、以下のようにたての長さ(連続一様分布での確率)を計算できます。
\(x(b-a)=1\)
\(x=\displaystyle\frac{1}{b-a}\)
面積が1であることを理解すれば、連続一様分布でなぜたて軸の値が\(\displaystyle\frac{1}{b-a}\)になるのか理解するのは難しくありません。
面積(積分)を利用し、期待値を計算する
確率密度関数\(f(x)\)を得た後は期待値\(E(X)\)を計算しましょう。連続一様分布の場合、期待値は以下の公式によって計算できます。
- \(E(X)=\displaystyle\frac{a+b}{2}\)
前述の通り、期待値はそれぞれの確率変数と確率をかけ、足すことによって得られます。ただ離散型確率分布とは異なり、連続型確率分布では明確な値(確率変数)を出すことができません。そこで面積(確率密度)を利用して確率変数を計算しましょう。
期待値の計算というのは、前述の通り\(x\)の値と発生確率(確率密度)Pをかけることによって得ることができます。連続一様分布では、確率Pは\(\displaystyle\frac{1}{b-a}\)です。
また\(x\)の値は決まっておらず、連続一様分布では\(a\)から\(b\)へと増えていくため、積分を利用して計算しましょう。シグマ\(\displaystyle\sum\)を利用して足すことができないため、代わりに積分\(\displaystyle \int\)をするのです。
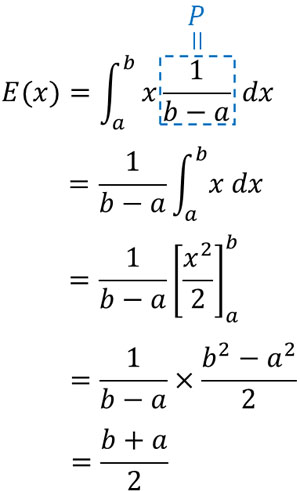
高校数学での積分の知識は必要になるものの、面積を計算することによって期待値の計算をすることができました。
連続一様分布での分散の公式を得る
期待値\(E(X)\)を計算することができたら、次は分散\(V(X)\)の計算をしましょう。連続一様分布での分散\(V(X)\)は以下の公式になります。
- \(V(X)=\displaystyle\frac{(b-a)^2}{12}\)
離散一様分布では、\(V(X)\)\(=E(X^2)-E(X)^2\)を利用することで分散を計算しました。同じように、連続一様分布でも分散の定義を利用して計算しましょう。

こうして、連続一様分布での分散\(V(X)\)を得る公式を計算できました。
面積(積分)を利用し、連続一様分布での累積分布関数を計算する
次に連続一様分布での累積分布関数を計算してみましょう。前述の通り、累積分布関数では確率を足していきます。離散型確率分布と連続型確率分布では、以下のように累積分布関数のグラフが異なります。
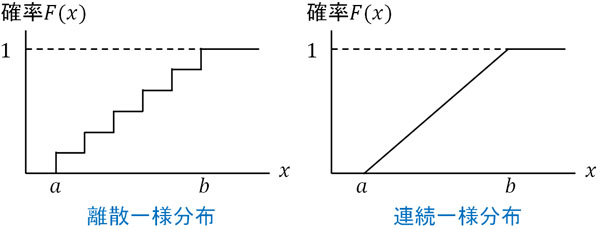
そこで連続一様分布での累積分布関数を得るため、面積を計算しましょう。累積分布関数では確率を足していくため、先ほど解説した通り、横軸の値(\(x\)軸の値)が増えていくに従ってたて軸の値も増えていきます。
確率を足すため、累積分布関数でのたて軸というのは、連続一様分布での面積に該当します。そこで、累積分布関数\(F(x)\)を出すために積分をしましょう。

連続一様分布の場合、確率は\(f(x)=\displaystyle\frac{1}{b-a}\)です。そのため、以下のように累積分布関数\(F(x)\)を計算しましょう。

こうして、\(a\)から\(b\)の範囲について、連続一様分布での累積分布関数\(F(x)\)は\(\displaystyle\frac{x-a}{b-a}\)になると計算できました。
なお、\(a<x\)の累積分布関数は0です。また、\(b<x\)での累積分布関数は1です。\(F(x)\)\(=\displaystyle\frac{x-a}{b-a}\)というのは、\(a\)から\(b\)までの範囲の関数を指しています。
一様分布の性質や公式を理解し、期待値や分散を計算する
最も単純な確率分布の一つが一様分布です。すべての確率が同じであり、コインやサイコロなど多くの場面で一様分布が存在します。
ただ、一様分布には離散一様分布と連続一様分布の2種類があります。そこで、それぞれのグラフの形を理解しましょう。離散型確率分布と連続型確率分布でグラフの形が異なるため、計算方法が違うのです。
また一様分布の期待値と分散を計算できるようになりましょう。高校数学の知識を利用すれば、離散一様分布と連続一様分布の期待値や分散を得る公式を導き出すことができます。難しい計算は必要なく、簡単な数列と積分を理解していれば計算できます。
一様分布はシンプルであるものの、利用される場面は多いです。そこで一様分布の性質や特徴、公式の出し方を理解しましょう。






