統計学で重要な検定法に二項検定とZ検定があります。両者は異なる検定法です。
二項検定では、起こる確率(p値)を直接計算することによって判定します。そのため、サンプル数が少ない場合に向いている検定法です。
一方でサンプル数が多い場合、すべての確率を計算するのは大変です。そこで二項分布を正規分布へ近似させ、確率の計算をします。標準正規分布を利用することで検定する方法をZ検定といいます。
二項検定を理解した後、Z検定を学びましょう。そうすれば、検定法の概念や違い、利用方法を理解できるようになります。
もくじ
二項分布では確率を直接計算できる
統計データを取るとき、多くの場面で二者択一です。例えば、以下のようになります。
- サイコロの目が1かどうか
- 週に一回以上、運動をするかどうか
- コインを投げ、表か裏か
このような場合、二項分布となります。以下が二項分布です。
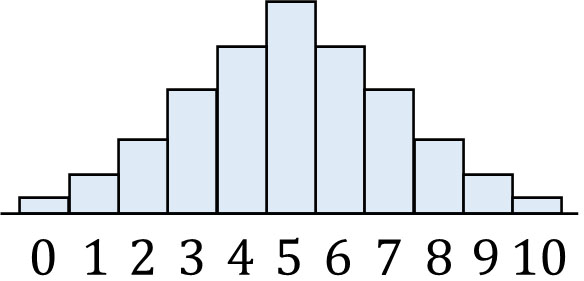
二項分布では真ん中の確率が最も高くなります。グラフの形が正規分布と同じであるのが二項分布なのです。
このとき、反復試行の確率を利用することによって、二項分布での確率を計算することができます。例えばサイコロを6回投げ、そのうち1の目が4回出ました。これは偶然でしょうか、それともイカサマがあったと考えるべきでしょうか。
※反復試行の確率を理解している前提で話を進めていきます。
帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:サイコロにイカサマなない(差はない)
- 対立仮説:サイコロにイカサマがある(差がある)
1の目が出る確率は\(\displaystyle\frac{1}{6}\)です。また、それ以外の目が出る確率は\(\displaystyle\frac{5}{6}\)です。そのため、以下の式によって確率を計算できます。
\(_6C_4\left(\displaystyle\frac{1}{6}\right)^4\left(\displaystyle\frac{5}{6}\right)^2≒0.0080\)
こうして、サイコロを6回投げて1の目が4回出る確率は0.0080(0.8%)とわかります。いずれにしても、このように直接確率を計算できるのです。
より極端な確率を計算し、確率をすべて足す
なお二項検定をする場合、より極端な確率をすべて計算し、足すようにしましょう。先ほどの例であれば、以下の確率をすべて計算して足す必要があります。
- サイコロを6回投げ、1の目が4回出る確率
- サイコロを6回投げ、1の目が5回出る確率
- サイコロを6回投げ、1の目が6回出る確率
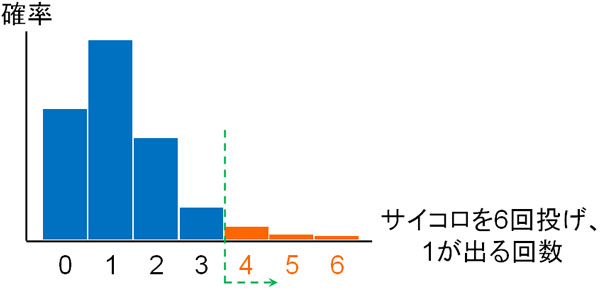
検定ではより極端なケースが出る確率をすべて足す必要があるため、二項分布で発生する極端なケースの確率も計算しましょう。
\(_6C_4\left(\displaystyle\frac{1}{6}\right)^4\left(\displaystyle\frac{5}{6}\right)^2≒0.0080\)
\(_6C_5\left(\displaystyle\frac{1}{6}\right)^5\left(\displaystyle\frac{5}{6}\right)^1≒0.00064\)
\(_6C_6\left(\displaystyle\frac{1}{6}\right)^6\left(\displaystyle\frac{5}{6}\right)^0≒0.000021\)
こうして、すべて確率を足すと約0.00866(0.87%)となります。
計算したp値と有意水準を比較する
確率(p値)を計算できれば、有意水準と比べることによって判定できます。サイコロを6回投げ、1の目が4回出る確率(1の目が5回または6回出る場合を含む)は0.00866(0.87%)です。
有意水準を0.05(5%)とする場合、計算したp値は0.00866であり、0.05よりも低いです。そのため5%以下で発生する稀なイベントが発生していると判断できます。そこで帰無仮説を棄却し、対立仮説を採用しましょう。
要は、確率を直接計算することによってp値を出し、有意水準0.05(または有意水準0.01)と比較することで検定する方法が二項検定です。二項分布では確率を直接計算するため、サンプル数が少ない場合に有意差の判定で有効です。
なお確率の計算をするとき、両側検定が可能な場合、両側確率を求めるのが一般的です。ただ今回は片側確率しか求めることができないため、片側検定によって有意差を判断しています。
標準正規分布を利用する場合はZ検定となる
一方でサンプル数が多い場合、一つずつ確率の計算をするのは大変です。そこで標準正規分布を利用して有意差の判定をしましょう。正規分布を利用することによって検定する方法をZ検定といいます。
二項検定では正規分布を利用せずに確率を計算します。一方、サンプル数が多い場合は二項分布を正規分布とみなして計算し、確率を求めることもできます。例えば、以下のケースを考えてみましょう。
- サイコロを1200回投げ、1の目が170回出ました。このサイコロにイカサマはあるでしょうか。
帰無仮説と対立仮説は先ほどと同じように以下のようになります。
- 帰無仮説:サイコロにイカサマなない(差はない)
- 対立仮説:サイコロにイカサマがある(差がある)
今回の例では、サイコロを投げる回数が多いです。この確率をすべて計算するのは大変なので、二項分布を正規分布へと近似させましょう。
二項分布を正規分布とみなす場合、以下の公式によって平均値を計算できることが知られています。

データ数(試行回数)は1200回であり、1の目が出る確率は\(\displaystyle\frac{1}{6}\)です。そのためサイコロを投げるとき、目の出る回数の平均(期待値)は200です。
\(1200×\displaystyle\frac{1}{6}=200\)
また二項分布の場合、正規分布への近似では以下の公式によって分散を計算できることがわかっています。
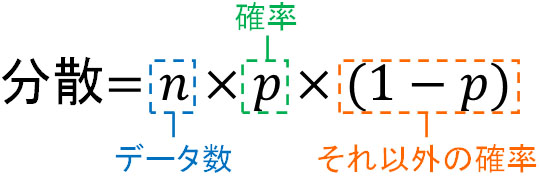
そのため、分散は166.7になります。
\(1200×\displaystyle\frac{1}{6}×\displaystyle\frac{5}{6}≒166.7\)
また、標準偏差は\(\sqrt{166.7}≒12.9\)です。こうして平均(期待値)と標準偏差を得ることができました。
平均と標準偏差がわかれば確率がわかる
正規分布での平均(期待値)と標準偏差がわかれば、標準正規分布に直すことによって確率を得ることができます。正規分布を標準正規分布に直すとき、以下の公式を利用することで確率変数Zを計算します。
- \(Z=\displaystyle\frac{X-μ}{σ}\)
そこで確率変数X(1の目が出た回数:170回)、平均値\(μ\)、標準偏差\(σ\)を代入すると以下のようになります。
\(Z=\displaystyle\frac{170-200}{12.9}≒-2.33\)
こうして、標準正規分布での確率変数Zは-2.33であるとわかります。そこでマイナスを取り、標準正規分布表から2.33となる確率を確認しましょう。そうすると、標準正規分布で確率変数Zが2.33となる確率は0.0099(0.99%)とわかります。
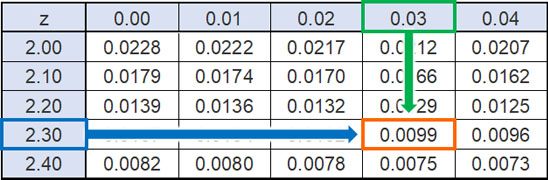
そこで有意水準を0.05(5%)とするとき、p値(0.0099)と比較すると、p値のほうが値は小さいです。そのため5%以下の確率で起こる稀なイベントが発生していると考えることができます。そこで帰無仮説を棄却し、対立仮説を採用しましょう。つまり、サイコロにイカサマがあると判断します。
二項検定を利用し、すべての確率を計算することによってもイカサマの有無を判断できます。ただそれだけ大変なので、正規分布を利用するZ検定を用いるのです。これにより、データ数が多くても有意差の判定が可能になります。
t検定やカイ二乗検定との違いと性質
なお二項検定やZ検定について、これらはt検定やカイ二乗検定とは性質が異なります。先ほど説明した通り、確率を直接計算して判定する場合は二項検定です。
一方で正規分布へ近似し、標準正規分布を利用して確率を出す場合はZ検定になります。二項分布に限らず、標準正規分布を利用する場合はZ検定となります。
これらに対して、t検定ではt分布を利用します。Z検定をする場合、正規分布を利用するため、母平均がわかっている必要があります。ただ母平均をわからないケースは多く、その場合はt分布を利用してt検定をするのです。
またカイ二乗検定では、適合度(予想される期待値とのズレ)やデータの独立性(それぞれの事象に関連性があるかどうか)を検定します。つまり、利用目的が大きく異なります。
また二項検定は直接確率を計算しますし、Z検定では標準正規分布表を利用して確率を得ます。そのためt検定やカイ二乗検定とは異なり、自由度を利用することはありません。つまり、検定法は大きく違います。
統計学では多くの検定法を学ぶことになります。そこで、これらの検定法の違いを理解しましょう。
二項検定とZ検定の性質や違いを学ぶ
統計学を学ぶとき、二項検定とZ検定をセットで理解しましょう。そうすれば、それぞれの性質や違いを理解しやすくなります。
二項分布では確率を直接計算できます。ただデータ数が多い場合、確率の計算は大変です。このとき統計学では、正規分布へ近似できる場合は「正規分布とみなして計算してもよい」というルールがあります。標準正規分布を利用して確率を出し、検定する方法をZ検定といいます。
二項分布に限らず、多くの分布を正規分布へと近似できます。標準正規分布を利用して確率を出すのであれば、どれもZ検定と呼ばれます。
二項検定とZ検定は最も基本的な検定法になります。統計学を学ぶとき、これらの違いや性質を理解しましょう。






