統計学の中でも、ベータ分布は内容が複雑です。グラフの形が変化するため、例を出しにくいのです。ベータ分布には一様分布が含まれますし、直線グラフもベータ分布の一つです。二次関数のグラフもベータ分布の一種です。
つまり、ベータ分布には多種多様なグラフの形があります。ただ多くのグラフの形があるからこそ、ベイズ統計でベータ分布がひんぱんに利用されます。つまりベイズ推定を学ぶためには、ベータ分布を学ばなければいけません。
それでは、ベータ分布の公式はどのようになっているのでしょうか。また、ベータ分布を利用して期待値を出すにはどうすればいいのでしょうか。
ベータ分布はさまざまな種類のグラフを含むため概念は難しいです。そこで、ベータ分布の特徴や公式の意味、ベイズ推定での利用法を解説していきます。
もくじ
一様分布でのベータ分布
ベータ分布は連続型確率分布の一つであり、結果が2つ(二者択一)の場合に利用されます。例えばコイン投げる場合、結果は表または裏の2つです。コイン投げは離散型確率分布であるものの、連続型確率分布の場合はベータ分布というわけです。
例として、子供の性別でベータ分布を学んでいきましょう。子供が男性または女性となる確率はいくらでしょうか。この確率については、当然ながらそれぞれ50%です。つまり、最初に子供が生まれる確率は50%で一定です。このように、常に確率が同じ分布を一様分布といいます。
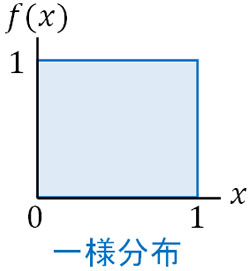
最も単純なベータ分布が一様分布です。一様分布というのは、特殊なベータ分布と理解しましょう。
因子が2つある場合での一様分布の確率
一方、父親が化学者の場合、女の子が生まれる確率はいくらでしょうか。多くの人は「あらゆるケースで子供の性別はそれぞれ50%」と考えるかもしれません。しかし、これは間違っています。確かに全体平均では、子供の性別はそれぞれ50%です。ただ、夫婦の状況によって子供の性別には偏りがあります。
例えば父親が有機化学者であったり、仕事で殺虫剤や医療用消毒剤をひんぱんに利用していたりする場合、女の子が生まれやすいと複数の論文で発表されています。この事実を踏まえ、父親が化学者の場合、「女の子を生みやすい夫婦」かもしれないのです。
つまり、夫婦の状況によって子供の性別に偏りがあります。そこで、以下の確率分布のグラフを考えましょう。
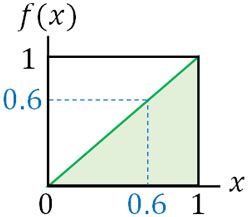
一様分布について、グラフを少し変えました。例えば「\(x\)軸の右へ行くほど、何らかの理由によって生まれる子供が女の子になりやすい」とします。\(x\)の値が0.6の場合、女の子が生まれる確率は0.6(60%)、男の子が生まれる確率は0.4(40%)です。
両方の確率を足すと1(100%)であるため、一様分布は成り立っています。ただ要素(因子)が2つあり、条件によって割合が変わる場合、このような図になります。
事前分布と事後分布を利用し、ベイズ推定を行う
ここまでの内容を基にしてベイズ推定をしましょう。ベータ分布はベイズ推定でひんぱんに利用されます。ベータ分布はグラフの形が決まっておらず、多種多様なグラフの形となります。そのため、ベイズ推定で好都合なのです。
先ほど、子供の性別について一様分布の図を作りました。何も情報がない場合、女の子が生まれる確率は50%です。ただ、「その夫婦の一人目の子供は女の子」という情報をあなたは得ました。この場合、その夫婦は女の子を授かりやすい性質があるのかもしれません。
この情報を得ることによって、先ほど提示したグラフのうち、「最初に男の子が生まれるケース」が排除されます。つまり、以下のようにグラフの形が変化します。
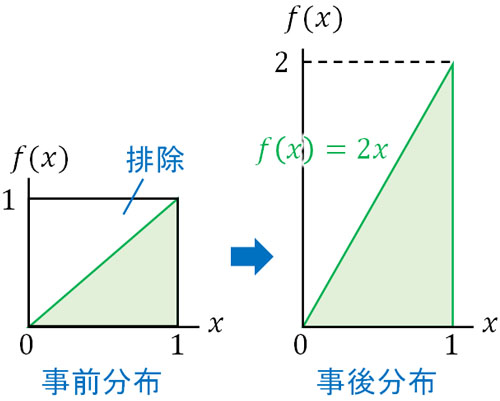
一様分布から「最初に男の子が生まれるケース」を排除する場合、グラフの形は四角形(一様分布)から直角三角形に変化します。またすべての面積(確率)が1(100%)になるように調節する必要があるため、三角形の面積を変形しましょう。そうすると、\(f(x)=2x\)\((0≤x≤1)\)の関数に変化します。
ベイズ推定を利用するとき、イベント発生によって確率が変化するため、グラフの形も変化するのです。今回の場合、一人目の子供が女性と判明したため、「二人目の子供が女の子である確率」が上昇しました。
ベータ分布での期待値を計算する
次に、期待値がどのように変化したのかを確認しましょう。横の長さが1の場合、期待値(平均)は重心に該当します。つまり、シーソーのバランスを取れる部分が期待値です。
一様分布の場合、すべての確率は同じであるため、重心は中心(0.5)です。そのため一様分布の期待値は0.5であり、女の子が生まれる確率は50%です。
一方、最初の子供が女の子と判明し、事後分布へとグラフが変化した場合はどうでしょうか。この場合、重心の位置は\(\displaystyle\frac{2}{3}≒0.667\)です。つまり、女の子が生まれる期待値(平均)は66.7%です。
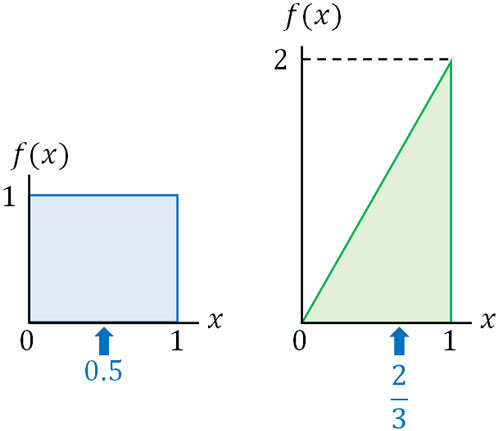
ベータ分布ではグラフの形が大きく変化し、それに伴って期待値も変化します。事後分布の期待値を確認すれば、イベントが発生する確率を推測できるようになります。
ベータ分布の確率密度関数の公式
次にベータ分布の公式を学びましょう。ベータ分布で確率密度関数\(f(x)\)を得る公式は以下になります。
- \(f(x)=Cx^{α-1}(1-x)^{β-1}\)\((0≤x≤1)\)
この公式は何を意味しているのでしょうか。Cは定数であり、重要ではありません。式によってCの値は変わり、ベータ分布ごとに決まった値が存在すると理解しましょう。
重要なのは\(α\)と\(β\)の値が変わることによって、確率密度関数が大きく変化することです。例えば\(α=1\),\(β=1\)の場合、\(f(x)=C\)となります。
- \(f(x)=Cx^0(1-x)^0=C\)\((0≤x≤1)\)
つまり、確率は常に同じです。これは一様分布を表しています。一様分布の場合、常に確率は一定です。一方で\(α=2\),\(β=1\)の場合はどうでしょうか。この場合、\(f(x)=Cx\)になります。
- \(f(x)=Cx^1(1-x)^0\)\(=Cx\)\((0≤x≤1)\)
先ほど示したような、右肩上がりの一次関数のグラフになります。
次に\(α=2\),\(β=2\)の場合を考えてみましょう。確率密度関数は\(f(x)=Cx(1-x)\)になります。
- \(f(x)=Cx^1(1-x)^1\)\(=Cx(1-x)\)\((0≤x≤1)\)
つまり、二次関数のグラフになります。ベータ分布では、\(α\)と\(β\)の値によってグラフの形が変わることを理解しましょう。
αとβの値によってベータ分布のグラフの形が変わる
それでは、どのようにベータ分布のグラフの形が変化するのでしょうか。具体的な値を\(α\)と\(β\)に代入し、グラフの形を確認しましょう。
なお前述の通り、すべての面積を1にする必要があります。そのため\(α\)と\(β\)によって定数Cの値は異なります。ただベータ分布の概念を理解するとき、定数Cは重要ではないため気にする必要はありません。
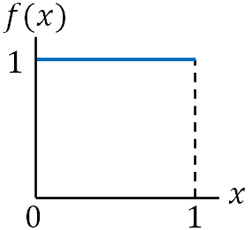
・\(α=1\),\(β=1\)の場合
確率密度関数は\(f(x)=1\)\((0≤x≤1)\)です。
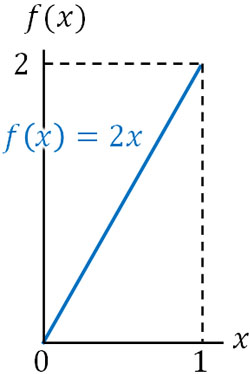
・\(α=2\),\(β=1\)の場合
確率密度関数は\(f(x)=2x\)\((0≤x≤1)\)です。
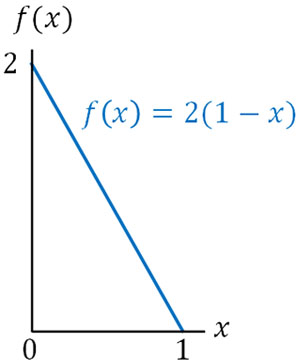
・\(α=1\),\(β=2\)の場合
確率密度関数は\(f(x)=2(1-x)\)\((0≤x≤1)\)です。
・\(α=2\),\(β=2\)の場合
確率密度関数は\(f(x)=6x(1-x)\)\((0≤x≤1)\)です。
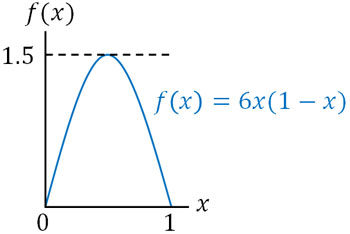
当然、\(α\)や\(β\)の値が大きくなると、グラフの形はより複雑になります。いずれにしても、ベータ分布ではさまざまなグラフの形へ変形できます。
ベータ分布で期待値\(E(X)\)を得る公式
なおベータ分布で期待値を得るとき、重心の場所が期待値になると解説しました。これを公式で表すとどのようになるのでしょうか。ベータ分布の期待値\(E(X)\)は以下の公式になります。
- \(E(X)=\displaystyle\frac{α}{α+β}\)
先ほど、一様分布では重心が中心となるため、期待値は0.5になると解説しました。そこで、\(α=1\),\(β=1\)を代入してみましょう。そうすると、以下のようになります。
\(E(X)=\displaystyle\frac{1}{1+1}=0.5\)
一方で\(α=2\),\(β=1\)の場合、\(f(x)=6x(1-x)\)\((0≤x≤1)\)の確率密度関数について、期待値は\(\displaystyle\frac{2}{3}\)になると解説しました。そこで、先ほどと同じように\(α=2\),\(β=1\)を代入しましょう。
\(E(X)=\displaystyle\frac{2}{2+1}=\displaystyle\frac{2}{3}\)
こうして、正しく計算できているとわかります。ベータ分布での期待値の計算というのは、あくまでも重心の計算式になります。シーソーのように、バランスの取れる位置が期待値です。
なおベータ分布で期待値を出す公式を計算するとき、積分をする必要があるので複雑です。そのため期待値を出す公式を証明したい場合、積分を学んだあとに証明してみてください。
事後分布を得るとき、関数が変化する
それでは、なぜベイズ統計学でベータ分布を理解することが重要なのでしょうか。この理由として、事前確率と事後確率でグラフの形が変化するからです。
例えばコインを一回投げる場合、表が出る確率は常に\(\displaystyle\frac{1}{2}\)です。つまり、一様分布です。一方でコインを何度も投げる場合、二項分布になります。以下のように、グラフの形が一様分布から二項分布へ変化するのです。
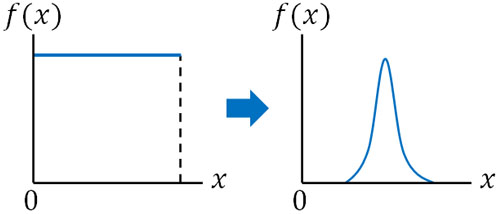
コインを投げる回数について、一回(事前確率)から多数(事後確率)に変えると確率分布が異なります。条件を変えることによってグラフの形が異なることはよくあります。そのため、ベイズ推定でベータ分布がひんぱんに利用されるのです。
事前分布としてベータ分布を利用することにより、特定のパラメーターをかけることによって事後分布(ベータ分布)を得ることができるのです。
重要なのは、事前分布と事後分布の両方ともベータ分布になることです。事前分布と事後分布で同じ分布の場合、ベイズ推定を利用することによる期待値や確率の計算が容易になります。グラフの形は大きく変わるものの、分布が同じであるため好都合なのです。
なお、事前分布と事後分布が同じとなるケースを共役事前分布といいます。ベータ分布は共役事前分布としてひんぱんに利用され、ベイズ推定で事後分布を得るときに有用です。
また事後確率の確率分布関数を得た場合、前述の方法によって期待値(平均)を計算することができます。ベータ分布での\(α\)と\(β\)の値がわかれば、関数が変化したとしても期待値の計算は簡単です。
成功数\(α\)や失敗数\(β\)の値が明らかな場合、ベータ分布を利用すれば、もっともらしい分布を得ることができます。また分布を得られるだけでなく、期待値や確率の計算など、データの分析が可能になるのです。
連続確率分布で利用されるベータ分布
グラフの形が決まっているわけではないため、ベータ分布の概念は難しいです。データによって\(α\)と\(β\)の値は変わり、それに伴ってベータ分布の形も変化します。
ただ重要なのは、\(α\)や\(β\)の値がわかっている場合、ベータ分布を利用して期待値や確率の計算を行えるようになることです。ベイズ推定をするとき、ベータ分布を利用することで事後分布の期待値の計算ができるのです。
多種多様なグラフの形を含むのがベータ分布です。ベータ分布の中には一様分布や二項分布、F分布、ガンマ分布、カイ二乗分布なども存在します。こうしたあらゆる分布を表せるのがベータ分布というわけです。
特定のグラフを表しているのがベータ分布ではありません。ただベータ分布の性質を利用すると、事前分布と事後分布で同じ分布を得られるため、ベイズ推定で便利というわけです。ベイズ推定でベータ分布を学ぶことになるため、ベータ分布とは何かについて、概念や公式の意味を理解しておきましょう。