モンティ・ホール問題と3囚人の問題：ベイズ推定での確率の変化

いくらの確率でイベントが起こるのかについて、直感と反するケースがよくあります。そうした中でも、モンティ・ホール問題や3囚人の問題は有名です。

これらはベイズ理論でひんぱんに利用される例題です。イベントが起こることによって確率が変化するとき、イベント発生後の確率を予想するのがベイズ推定です。ベイズ推定は条件付き確率でもあり、特定条件の発生によって確率が上昇したり下がったりするのです。

モンティ・ホール問題と3囚人の問題を学べば、私たちの直感は多くのケースで間違っていることがわかります。また、どのように確率が変化するのかも理解できます。

ベイズ推定で深く関係しているのがモンティ・ホール問題と3囚人の問題です。そこでこれらの例題を利用して、私たちの直感と反する現象がどのように起こるのか確認していきましょう。

1 直感と反するモンティ・ホール問題
- 1.1 極端な例を利用するとモンティ・ホール問題を理解できる
- 1.2 ベイズ推定（ベイズ定理）でのモンティ・ホール問題
2 3囚人の問題で考えるベイズ定理
- 2.1 どのケースで確率が上昇するのか学ぶ
3 モンティ・ホール問題と3囚人の問題から学ぶベイズ理論

直感と反するモンティ・ホール問題

条件付き確率の問題であり、ベイズ定理を利用した例題としてモンティ・ホール問題は非常に有名です。モンティ・ホール問題は以下のようになります。

3つのドアがあり、そのうち一つが正解です。そこで、あなたは正解と考える一つのドアを選びました。その後、司会者は答えを知っており、不正解のドアを一つ開けました。あなたは2つのドアを自由に選べます。あなたは最初に選んだドアを変えますか？

モンティ・ホール（Monty Hall）が司会者のアメリカのゲームショー番組で取り上げられた問題です。もし正解のドアを選べば、新車を得ることができます。もし、あなたが選ぶドアを変える場合、正解確率は上がるでしょうか。

多くの人は、ドアを変えたとしても正解の確率は同じと考えます。2つのドアのうち、一つが正解です。そのため、確率は\(\displaystyle\frac{1}{2}\)です。

ただ実際には異なります。選ぶドアを変えると、正解の確率が\(\displaystyle\frac{1}{3}\)から\(\displaystyle\frac{2}{3}\)へ変化します。つまり、新車を得られる確率が2倍になります。なぜ、このような奇妙な事態になるのでしょうか。

モンティ・ホール問題について、多くの人が「ドアを変えても確率は変わらない」と反論しました。反論した人の中には著名な数学者が何人も含まれていました。つまり大学で数学を教えている教授であっても、ベイズ推定を理解していない場合、直感に反するイベントについて数学的に解答せずに結論を述べるということです。

当然、ベイズ統計学について詳しくない私たちがモンティ・ホール問題の結論を受け入れにくいと考えるのは当然です。そこで、なぜ選ぶドアを変えることによって正解となる確率が上昇するのか確認していきましょう。

極端な例を利用するとモンティ・ホール問題を理解できる

なぜ、モンティ・ホール問題を生じるのでしょうか。先ほど、3つの選択肢を含む問題が出されました。そこで、より極端なケースを考えてみましょう。そうすれば、なぜ選択肢を変えると正解となる確率が上昇するのかわかります。

あなたの目の前に100枚のカードがあります。あなたはカードを1枚引きました。その後、司会者は不正解である98枚のカードを捨てました。あなたはカードを変えますか？

最初に選んだカードが正解である可能性は\(\displaystyle\frac{1}{100}\)です。つまり、不正解を選んでいる可能性が圧倒的に高いです。その後、司会者が98枚の不正解のカードを捨てます。その場合、残ったカードが正解である可能性は非常に高いです。

このように極端な例で考えると、なぜカードを変更すると正解を得られる可能性が高くなるのか容易に理解できます。

ベイズ推定（ベイズ定理）でのモンティ・ホール問題

それでは、より数学的にモンティ・ホール問題を考えていきましょう。モンティ・ホール問題というのは、前述の通りベイズ定理を利用しています。

特定のイベントが発生することによって、確率が変わることを利用する統計学がベイズ統計学です。ベイズ統計学はベイズ定理を基本としており、ベイズ定理を利用して確率を予測することをベイズ推定といいます。

ヒントなしの状態では、モンティ・ホール問題正解を得られる確率は\(\displaystyle\frac{1}{3}\)です。これについては、全員が納得すると思います。

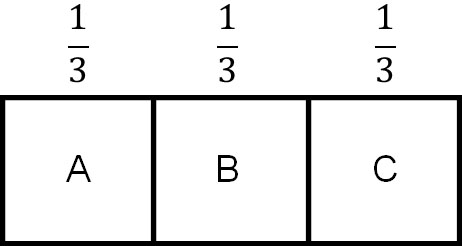
次に、司会者が不正解のドアを開けます。あなたが最初にどのドアを選ぶのかは不明ですが、いずれにしても不正解のドアを司会者はあなたに教えるのです。こうして、「司会者が不正解のドアを開ける」ことによってその後の確率が変化します。

仮にあなたがAを選ぶ場合、その後に「50%の確率で司会者がBのドアを開ける（A＆開B）」または「50%の確率で司会者がCのドアを開ける（A＆開C）」となります。そのため、あなたがドアAを選ぶ場合は以下のようになります。

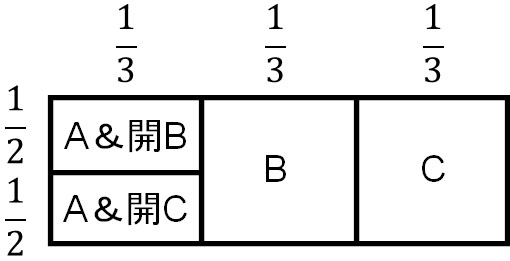
もちろんあなたがドアBを選んでも、ドアCを選んでも同じ結果となります。ひとまず、今回はドアAを選んだと仮定しましょう。

次に、司会者がBまたはCのドアを開けます。例えば司会者が不正解のドアとしてドアCを開ける場合、以下のようになります。

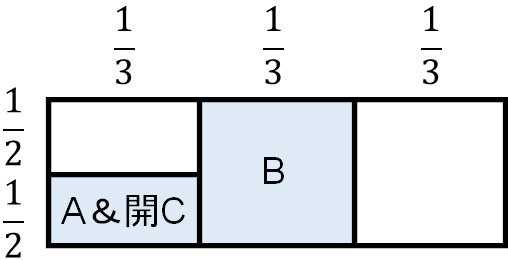
ドアCが不正解とわかったため、選択肢からドアCとA＆開Bを排除しましょう。そうすると、ドアAが正解の確率は全体に対して\(\displaystyle\frac{1}{3}×\displaystyle\frac{1}{2}=\displaystyle\frac{1}{6}\)です。一方、Bが正解の確率は全体に対して\(\displaystyle\frac{1}{3}\)です。

またベイズ推定では、イベント発生後の確率（事後確率）について、すべての確率を合計して1（100%）にします。そこで\(\displaystyle\frac{1}{6}:\displaystyle\frac{1}{3}\)の割合のまま、合計が1になるように調節しましょう。そうすると、\(\displaystyle\frac{1}{3}:\displaystyle\frac{2}{3}\)になります。

つまりドアAを選ぶ場合、正解の確率は\(\displaystyle\frac{1}{3}\)です。それに対して、選択をドアBに変える場合は正解の確率が\(\displaystyle\frac{2}{3}\)に上昇します。

3囚人の問題で考えるベイズ定理

ベイズ定理を利用する例題について、もう一つ重要なのが3囚人の問題です。3囚人の問題を学べば、ベイズ理論にて確率がどのように変化するのか理解できるようになります。

モンティ・ホール問題と3囚人の問題は本質的に同じ内容です。ただ別の角度からベイズ定理を捉えることができるようになるため、ベイズ推定を学ぶ場合、モンティ・ホール問題だけでなく3囚人の問題も習うのが一般的です。

3囚人の問題は以下になります。

囚人A、囚人B、囚人Cがいます。3人のうち2人は処刑され、1人は釈放されます。本人には、釈放されるかどうか知らされません。そこで囚人Aは「自分以外のうち、どちらが処刑されるのか教えてほしい」と看守に尋ねました。すると、看守は「囚人Bが処刑される」と答えました。
囚人Aは喜びました。囚人Bが処刑される場合、残ったのは自分と囚人Cです。2人が残っているため、自分が生き残る確率は\(\displaystyle\frac{1}{2}\)と囚人Aは考えました。この考え方は正しいでしょうか。

先に答えをいうと、この考え方は間違っています。囚人Aが生き残れる確率は\(\displaystyle\frac{1}{2}\)ではなく、\(\displaystyle\frac{1}{3}\)です。つまり、囚人Aの生存確率は変わっていません。なぜ、このような事態に陥るのでしょうか。

前述の通り、3囚人の問題はモンティ・ホール問題と本質的に内容が同じです。そこで、3囚人の問題を解き明かしていきましょう。

どのケースで確率が上昇するのか学ぶ

モンティ・ホール問題でも3囚人の問題でも、イベント発生後に確率が変化します。このとき、どのように確率が変化するのでしょうか。確率が変化するとき、3囚人の問題では以下の2パターンを思いつきます。

釈放されるのは囚人Aまたは囚人Cなので、囚人Aの生存確率は\(\displaystyle\frac{1}{2}\)になる。つまり、生存確率は\(\displaystyle\frac{1}{3}\)から\(\displaystyle\frac{1}{2}\)へ上昇する。
囚人Bが処刑されるとわかっても、囚人Aの生存確率は\(\displaystyle\frac{1}{3}\)で変わらない。一方、囚人Cの生存確率は\(\displaystyle\frac{1}{3}\)から\(\displaystyle\frac{2}{3}\)へ上昇する。

ベイズ理論では、後者の考え方が正しいとされています。つまり「囚人Bが処刑される」と囚人Aが知ったとしても、囚人Aの生存確率は変わりません。

この理由としては、先ほどモンティ・ホール問題で解説しました。最初の状態では、あなたがどのドアを選んでも、正解を当てる確率は\(\displaystyle\frac{1}{3}\)です。例えばドアAを選んで正解となる確率は\(\displaystyle\frac{1}{3}\)です。

次に、司会者はドアCが不正解と明らかにしました。これにより、以下のように確率が変化すると解説しました。

ドアAのままでは、正解を得る確率は\(\displaystyle\frac{1}{3}\)です。一方でドアBに変える場合、正解の確率は\(\displaystyle\frac{2}{3}\)です。つまり、ドアAを選んでいる状態では確率は変化しません。ドアBに変えることによって、正解の確率が2倍に増えて\(\displaystyle\frac{2}{3}\)になるのです。

これを3囚人の問題に置き換えると、「囚人Bが処刑される」と囚人Aが知ったとしても、囚人Aの生存確率は上昇しません。

ここまでの解説についても、極端な例を考えるとわかりやすいです。100枚のカードを引くとき、前述の通り正解を得る確率は\(\displaystyle\frac{1}{100}\)です。つまり、正解になる可能性は低いです。

次に、司会者が不正解のカードを98枚捨てました。この場合、あなたの手元には2枚のカードがあります。ただ、あなたが最初に選んだカードについて、正解の確率が\(\displaystyle\frac{1}{2}\)に上昇するかというと、当然ながらそのようなことは起こりません。最初に選んだカードの確率は\(\displaystyle\frac{1}{100}\)のままです。

一方、あなたがどのカードを選ぼうが司会者は不正解のカード98枚を捨てます。あなたは\(\displaystyle\frac{99}{100}\)の確率で不正解のカードを最初に選び、そのあとに司会者が98枚のカードを捨てるのです。当然、あなたが選ばなかったカードが正解である確率は非常に高いです。

イベント発生によって確率が変わるものの、すべての確率が変化するわけではありません。確率が変化しない要素があれば、確率が変わる要素もあるのです。モンティ・ホール問題と3囚人の問題を学べば、どのように要素の確率が変わるのか理解できるようになります。