統計学で最も重要な分布が正規分布です。当然、ベイズ統計学についても正規分布を利用して統計処理するケースがひんぱんにあります。
多くの現象は正規分布に従います。そのためベイズ推定によって事後確率を得たい場合、正規分布でのベイズ推定の方法を理解しなければいけません。
正規分布を利用してベイズ推定を行う場合、期待値や分散の計算を含めて理解しましょう。あらゆる場面で正規分布でのベイズ推定が活用されています。将来の予測をするとき、ベイズ推定は有効なのです。
それでは、どのように正規分布を利用してベイズ推定をすればいいのでしょうか。正規分布を活用してベイズ推定をする方法を解説していきます。
もくじ
共役事前分布により、事前分布が正規分布だと事後分布も正規分布となる
多くのデータは正規分布となります。例えば成人男性の身長を測定するとき、データの範囲として140~220cmを想定する人はいません。一方、160~180cmの身長を想定するのは一般的です。成人男性の身長を調べるとき、平均身長の周辺にあるデータが最も多くなります。
ただ、条件が加わると平均身長は変化します。例えば成人男性のデータがアジア人の場合、平均身長は低くなります。一方、データが欧米人の場合、170~190cmの身長を想定するかもしれません。
このとき、ベイズ推定では必ず事前分布と事後分布が存在します。イベント発生によって、事後分布を得ることになるのです。
ベイズ推定をするとき、事前分布と事後分布が同じ分布であると非常に好都合です。そうしたとき、正規分布を利用する場合は事前分布と事後分布が同じになります。この性質を共役事前分布といいます。
例えば成人男性の身長データがアジア人とわかっても、正規分布に従うことは容易に想像できると思います。ベイズ推定を利用するとき、事前分布と事後分布が同じなのは非常に都合がよいのです。
ベイズ推定を利用して事後確率を得る手順
それでは、実際にベイズ推定を利用して事後確率を計算しましょう。例えば、以下の場面を考えます。
- 成人男性の平均身長が170cmであり、標準偏差を10とします。ただ8人を調べたとき、平均身長は180cmであり、標準偏差は5でした。このデータから、母集団の平均身長はいくらと予想できますか?
事前分布と事後分布は両方とも正規分布です。ただ標本では平均身長が高く、以下のように事後分布は右にズレるとわかります。
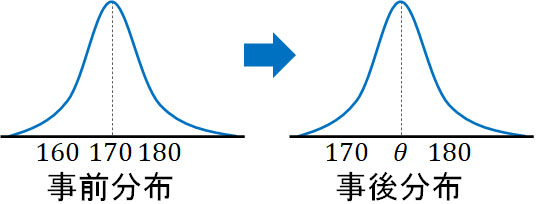
事前の情報(事前分布)と実測値が異なるのは普通です。そこで、実測値を用いて母集団(事後分布)を予測するのです。
このとき、事後分布の期待値(平均)を\(θ\)とします。つまり\(θ\)を出すことができれば、母集団の平均身長がわかります。
正規分布で事後分布の期待値(平均)を得る公式
それでは、どのようにして事後分布の期待値(平均)を出せばいいのでしょうか。正規分布で事後分布の期待値を得る場合、少し複雑な公式を利用することになります。
公式が複雑であるため、当然ながら公式の証明をするのは大変です。そのため公式の証明をしたい場合、大学数学を学んだあとに興味のある人のみ行いましょう。
事前分布の平均を\(μ_0\)、標準偏差を\(σ_0\)とします。また測定したデータ\(x\)について、事後分布の正規分布の平均を\(θ\)、標準偏差を\(σ\)とします。
この場合、事後確率は「データ\(x\)が観測されている下で、正規分布の平均\(θ\)を得られるケース\(p(θ|x)\)」になります。正規分布\(p(θ|x)\)の期待値(平均)は以下の公式を利用して計算します。
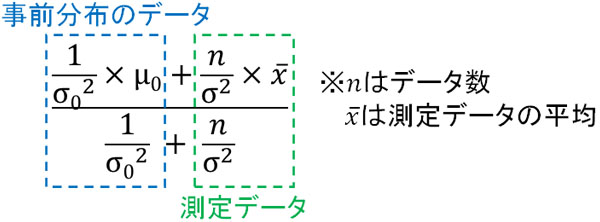
そこで、この公式に値を当てはめましょう。以下のようになります。
\(\displaystyle\frac{\displaystyle\frac{1}{10^2}×170+\displaystyle\frac{8}{5^2}×180}{\displaystyle\frac{1}{10^2}+\displaystyle\frac{8}{5^2}}\)
\(≒179.69\)
こうして、正規分布\(p(θ|x)\)の期待値(平均)は179.69とわかりました。事前分布と測定データを利用することによって、事後分布の期待値を得ることができるのです。
サンプルサイズが大きいと正確になる
なおサンプルサイズ(サンプル数)が1の場合、\(n=1\)になります。先ほどと同じ条件について、データ数を1として計算すると以下のようになります。
\(\displaystyle\frac{\displaystyle\frac{1}{10^2}×170+\displaystyle\frac{1}{5^2}×180}{\displaystyle\frac{1}{10^2}+\displaystyle\frac{1}{5^2}}\)
\(=178\)
サンプルサイズが8の場合、前述の通り事後分布の期待値は179.69です。一方でサンプルサイズが1の場合、事後分布の期待値は178です。
当然ながら、データ数が多いほど信頼性の高い標本となります。そのため試行回数が多くなるにしたがって、標本が事後分布に与える影響は大きくなります。つまり、データ数が多いとより正確な事後分布の平均値を得られると理解しましょう。
過去のデータと最新データの両方を利用し、未来を予測する
ベイズ推定がなぜ多くの場面で利用されるかというと、未来の予測が可能になるからです。過去のデータ(事前分布)を利用し、最新データ(得た情報)を活用することによって、未来の予測(事後分布)ができるのです。
例えば物流は交通渋滞の影響を大きく受けます。到着時間を予測するとき、過去のデータと最新データ(地震によって交通機関が乱れているなど)を組み合わせる必要があります。過去のデータだけ、または最新データだけを利用して正確な未来の予測はできません。
また飛行機会社や船会社が予約状況の予測をする場合、過去データと最新データ(天気予報など)を利用して未来の予約状況を予測することが可能になります。
世の中のほとんどのデータは正規分布に従うため、正規分布を利用してベイズ推定をすることは多くの場面で役に立ちます。このように過去データと最新データを利用して、期待値(平均)を得ることで将来の予測をしてみてください。






