データを得られたとき、データに差があるのかどうかを証明するためには、統計処理をする必要があります。このとき頻繁に利用されるのがt検定です。母集団の平均値(母平均)や分散(母分散)がわからなかったとしても、集めたデータ(標本)を利用することによって検定が可能です。
ただt検定には複数の種類があります。一標本t検定と二標本t検定が存在し、この二つの違いを見極めるようにしましょう。
また二標本t検定をするとき、「対応のあるt検定(関連二群)なのか、それとも対応のないt検定(独立二群)なのか」によって計算方法が異なります。そのため、どのような群を検定したいのか見極めなければいけません。
統計学で最も利用される方法がt検定です。そこで、どのようにt検定をすればいいのか解説していきます。
もくじ
標本だけを利用し、母平均の推定が可能なt分布
t検定ではt分布を利用することによって検定をします。t分布は正規分布と似た形状のグラフであり、正規分布とt分布を比べると以下のようになります。
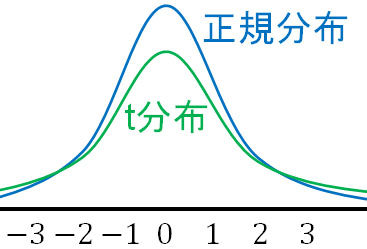
本来、正規分布を利用して有意差を確認するほうが正確です。ただ正規分布を利用するためには、母平均がわかっていなければいけません。
一方、母平均がわからなくても計算できる方法がt分布です。カイ二乗分布を利用することによって、母平均の推定が可能です。母集団が正規分布するとわかっており、標本として少数サンプルを利用するとき、t検定によって統計処理するのが有効です。
なお正規分布に従う統計学的な操作をパラメトリック検定といいます。t分布は正規分布と形が似ており、正規分布の性質を利用して統計処理します。そのため、t検定はパラメトリック検定に分類されます。
片側検定・両側検定を見極めてp値を出し、有意差を確認する
t検定をするとき、片側検定をしたいのか、それとも両側検定をしたいのか見極めるようにしましょう。p値を計算するとき、片側検定と両側検定では値が大きく異なります。当然、有意差を確認するときの結果も変わります。
例えば体重の異常を確認するとき、「肥満の人」「やせこけている人」を含める場合、両側検定になります。有意水準0.05で判断する場合、異常値は両側それぞれ0.025(2.5%)で設定します。
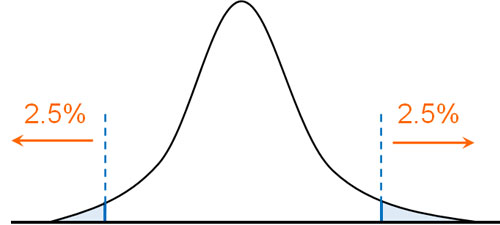
一方で肥満の人のみを対象に判断したい場合、片側検定になります。有意水準0.05で判断する場合、体重の重い人について0.05(5%)で判定します。
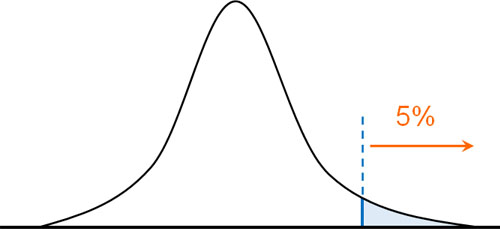
t検定をするとき、まずは前提条件を確認しましょう。前提条件が間違っていると、正しく有意差を出せていないことになります。
なお片側検定よりも、両側検定のほうが条件の厳しい検定となります。右側(または左側)の帰無仮説の棄却域が狭くなるからです。そのため両側検定で有意水準を設定し、帰無仮説を棄却できるのであれば、結果に問題はないといえます。
一標本t検定と二標本t検定の違いは何か
なおt分布・t検定はゴセットという化学者によって発見されました。彼はスチューデントというペンネームによって論文投稿したため、t検定はスチューデントのt検定とも呼ばれています。
t検定には複数の種類があります。以下のようになります。
- 一標本t検定
- 対応のある二標本t検定(関連二群)
- 対応のない二標本t検定(独立二群)
t検定を理解するためには、この違いを学ばなければいけません。ただ概念は難しくはないです。
一標本t検定とは、一つの標本を利用して検定する方法になります。標本について、母平均と比較して「通常では観測されない異常値が観測されているかどうか」を判定するのが一標本t検定です。
一方で二標本t検定では、二つの標本を利用して差があるかどうかを確認します。このとき対応のある二標本t検定(関連二群)では、同じ個体(同じ人、同じ動物、同じ物など)を利用して比較するときに利用されます。
例えば同じ人について、「薬の飲む前と飲んだ後の血圧を比較する」という場合、対応のある二標本t検定を利用します。
一方で同じ個体を比較しない場合、対応のない二標本t検定(独立二群)となります。例えばクラスごとにテストの点数を比較する場合、同じ人を利用して比較するのではなく、異なる人を比較するため、対応のない二標本t検定を利用します。
いずれにしても、標本の種類によって利用するt検定が異なることを理解しましょう。
※ここからは「t分布について理解している」という前提で話を進めていくため、t分布を理解していない場合、t検定の前にt分布を学びましょう。
一標本t検定での統計処理
それでは、実際にt検定をしてみましょう。標本平均や標本分散(不偏分散)を計算すれば、母平均の推定が可能です。つまり、t分布によって母平均の95%信頼区間(または99%信頼区間)がわかります。
母平均が95%のデータ(または99%のデータ)範囲に含まれるかどうかを確認することによって、標本データが異常であるかどうか(通常と比べて差があるかどうか)を確認できます。これがt検定です。
なお標本平均を\(\overline{X}\)、母平均を\(μ\)、自由度を\(n\)、標本標準偏差(不偏標準偏差)を\(s\)とすると、t分布での統計量Tは以下の式によって表すことができます。

そこで、一標本t検定ではこの公式に値を代入しましょう。例えば、以下の問題の答えは何でしょうか。
- 一つ20gと表示されているお菓子があります。10個のお菓子の重さを一つずつ測定すると、以下の結果でした。一つ20gという表示は正しいでしょうか、それとも虚偽でしょうか。
| 19g | 21g | 18g | 24g | 20g |
| 17g | 15g | 21g | 18g | 22g |
まず、帰無仮説・対立仮説と作りましょう。以下のようになります。
- 帰無仮説:お菓子の一つの重さに差がない
- 対立仮説:お菓子の一つの重さに差がある
母平均\(μ\)は20gであり、その他の値を計算すると以下のようになります。
- 標本平均\(\overline{X}=19.5\)
- 自由度(サンプル数)\(n=10\)
- 標本標準偏差(不偏標準偏差)\(s=2.64\)
\(T=\displaystyle\frac{(19.5-20)×\sqrt{10}}{2.64}≒-0.6\)
なおt分布は自由度\((n-1)\)に従います。それでは自由度\((10-1=)9\)のとき、95%信頼区間のTはいくらでしょうか。すべての統計学の教科書では、有意水準を0.05(5%)または0.01(1%)とするときの統計量Tの値が掲載されています。そこで自由度9のとき、0.05となるTの値を確認すると2.262と確認できます。
つまり自由度9のときの95%信頼区間(両側検定)は\(-2.262≦T≦2.262\)です。この間に計算した統計量Tがある場合、全体のうち「95%のデータが含まれている範囲」に推定される母平均が存在するため、帰無仮説を採用します。
一方で計算した統計量Tが\(-2.262≦T≦2.262\)の範囲にない場合、5%以下の確率で起こる事象が偶然に発生したと考えるのは不自然です。そこで帰無仮説を棄却し、対立仮説を採用します。
今回の場合、統計量\(T=-0.6\)であり、\(-2.262≦T≦2.262\)に含まれます。そのため標本平均は19.5gであり、20gと異なるものの、偶然に起こった現象と捉えることができます。そのため帰無仮説を棄却できず、「20gという表示は正しい」と判断します。
対応のある二標本t検定(関連二群)での検定
t分布について理解している場合、一標本t検定の内容は問題なく把握できると思います。それでは、対応のある二標本t検定(関連二群)の検定はどのようにすればいいでしょうか。
前述の通り、同じ個体(同じ人間や動物、物)を利用して比較するとき、対応のある二標本t検定を活用します。このとき、同じ個体について差を利用しましょう。引き算することによって得た値を\(d\)とすることにより、前後で変化があったかどうかを確認するのです。
同じ個体について、測定前と測定後で変化がない場合、2つの群の差は0になります。つまり\(d\)が0に近い場合、差がないと判断します。一方で\(d\)が大きなプラスの値(またはマイナスの値)の場合、差があると判断します。
このとき、利用する公式は先ほどと同じ以下を利用します。
- \(T=\displaystyle\frac{(\overline{X}-μ)×\sqrt{n}}{s}\)
データの差\(d\)を利用するため、標本平均\(\overline{X}\)の代わりとして、データの差の平均値\(\overline{d}\)を利用しましょう。またデータに差がないと仮定する場合、母平均は\(μ=0\)になります。測定の前と後で差がないため、引き算をすると当然ながら値は0であり、母平均も0になります。
そのため対応のある二標本t検定の場合、以下のように公式を変えることができます。
- \(T=\displaystyle\frac{\overline{d}×\sqrt{n}}{s}\)
関連二群の二標本t検定では、この公式を利用することによって検定しましょう。例えば以下の問題の答えは何でしょうか。
- ソフトウェアをインストールして、パソコンのスピードがどれだけ上昇するかテストしました。以下の結果のとき、ソフトウェアに効果があるかどうか調べましょう。
| 前 | 後 | 差(\(d\)) |
| 1000 | 1010 | 10 |
| 950 | 980 | 30 |
| 1100 | 1110 | 10 |
| 800 | 850 | 50 |
| 950 | 990 | 40 |
| 750 | 800 | 50 |
| 1080 | 1100 | 20 |
まず、帰無仮説と対立仮説を設定しましょう。
- 帰無仮説:ソフトウェアをインストールしてもスピードに差はない
- 対立仮説:ソフトウェアをインストールするとスピードに差がある
次に、標本の差の平均値\(\overline{d}\)と標本の差の分散\(s\)を求めましょう。計算方法は省略しますが、エクセルなどを利用すると以下のように計算できます。
- 標本の差の平均値\(\overline{d}=30\)
- 標本標準偏差(不偏標準偏差)\(s≒17.32\)
またサンプル数(自由度)\(n\)は7です。そのため、統計量Tは以下のようになります。
\(T=\displaystyle\frac{30×\sqrt{7}}{17.32}≒4.582\)
自由度\((n-1=)6\)の場合、t分布で95%信頼区間(両側検定)を確認すると、\(-2.447≦T≦2.447\)です。そのため統計量Tと有意水準0.05(5%)を比べると、統計量Tは4.582であるため、\(-2.447≦T≦2.447\)の範囲に含まれていないことがわかります。
つまり先ほどの結果は5%以下の確率で起こる事象であり、こうしたケースが偶然に起こるとは考えにくいです。そこで帰無仮説を棄却し、対立仮説を採用します。要は、「有意差があり、ソフトウェアは効果的である」と結論付けることができます。
参考までに、今回の例題について95%信頼区間ではなく、99%信頼区間で検定してみましょう。統計学の教科書を開くと、自由度6のとき、有意水準0.01(1%)となるT値(両側検定)は\(-3.250≦T≦3.250\)です。
統計量Tは4.582であるため、\(-3.250≦T≦3.250\)に含まれていません。そのため有意水準0.01で検定したとしても、このソフトウェアは優れる効果があると判断できます。
スチューデントのt検定を利用できる条件が等分散
ちなみに二標本t検定を行う場合、等分散であるかどうかを確認しましょう。等分散というのは、要は「データの形が同じかどうか」を確認することを指します。グラフの形が似ている場合は等分散であり、グラフの形が似ていない場合は不等分散です。
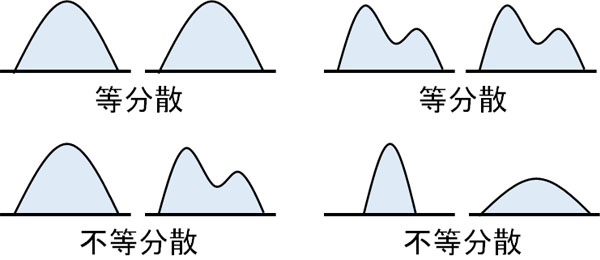
等分散かどうかを確認する方法にF検定があります。そのためスチューデントのt検定をするためには、事前にF検定をする必要があります。
一標本t検定の場合、F検定をする必要はありません。一つの標本を利用して統計処理するため、グラフの形は関係ないのです。一方で二標本t検定をする場合、グラフの形が同じである必要があります。
それではF検定を行い、等分散ではない場合はどのように判断すればいいのでしょうか。この場合、スチューデントのt検定を利用することはできません。スチューデントのt検定というのは、2つの標本が互いに等分散であるという前提条件があるのです。
等分散の確認は必要?ウェルチのt検定で確認なしに検定をする
それでは、等分散でない場合は統計処理をすることはできないのでしょうか。この場合、ウェルチのt検定を利用します。ウェルチのt検定では、2つの標本が互いに等分散かどうかに関係なく利用することができます。
つまりウェルチのt検定の場合、等分散であっても、等分散でなくても利用可能です。そのため教科書的には、以下の順番によってt検定を行うと記されていることがよくあります。
- F検定を行い、等分散かどうかを確認
- 等分散の場合、スチューデントのt検定を行う
- 等分散でない場合、ウェルチのt検定を行う
それでは必ずF検定を行う必要があるかというと、必ずしもそうではありません。最初からウェルチのt検定をしても問題ないです。この場合、F検定をスキップすることができます。そのため実際のところ、スチューデントのt検定をしなくてもいいというわけです。
ただ統計学を学ぶ場合、スチューデントのt検定は最も基礎的な内容になります。そのためウェルチのt検定を学ぶ前に、スチューデントのt検定を理解しなければいけません。
二標本t検定での統計処理:対応のないt検定(独立二群)
次に、対応のない二標本t検定の統計処理方法について確認していきましょう。前述の通り、スチューデントのt検定では等分散である必要があります。そこで、標本が等分散であるという前提で解説していきます。
対応のないt検定(独立二群)では、異なる個体を比較します。この検定方法としては、2つの標本の差を利用しましょう。
t分布を利用することによって母平均の推定が可能です。そこでt検定を利用し、2つの標本について母平均の差を検討するのです。
対応のあるt検定では、差を直接利用することによって統計処理をしました。一方で対応のない標本の場合、同じ個体ではないので引き算をすることはできません。そこで標本1と標本2について、それぞれ母平均を計算して引き算するのです。
帰無仮説では、「2つの群に差がない」と仮定します。差がない場合、母平均の引き算をすると統計量Tは0になります。一方で差がある場合、標本1と標本2の母平均は異なります。そのため、母平均の差を表す統計量Tは0よりも大きい値(または小さい値)になります。
・二群の差の公式を得る
なお対応のあるt検定について、以下の公式を利用すると説明しました。
- \(T=\displaystyle\frac{(\overline{X}-μ)×\sqrt{n}}{s}=\displaystyle\frac{\overline{X}-μ}{\displaystyle\frac{s}{\sqrt{n}}}\)
そこで\(T=\displaystyle\frac{\overline{X}-μ}{\displaystyle\frac{s}{\sqrt{n}}}\)を利用し、母平均の差を計算しましょう。
そこで標本1を\(T_1=\displaystyle\frac{\overline{x}_1-μ_1}{\displaystyle\frac{s_1}{\sqrt{n_1}}}\)、標本2を\(T_2=\displaystyle\frac{\overline{x}_2-μ_2}{\displaystyle\frac{s_2}{\sqrt{n_2}}}\)とするとき、母平均の差は以下のようになります。
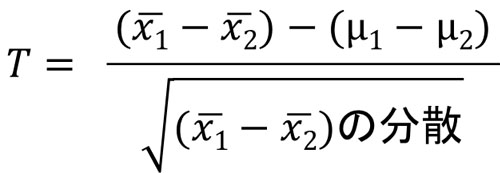
※\(\overline{x_1}\)は標本1の平均値であり、\(\overline{x_2}\)は標本2の平均値です。
また2つの群について、独立の場合の差は以下のようになります。
\(T=\displaystyle\frac{(\overline{x}_1-\overline{x}_2)-(μ_1-μ_2)}{s\sqrt{\displaystyle\frac{1}{n_1}+\displaystyle\frac{1}{n_2}}}\)
なぜ、このような式になるのかは詳細を省きます。非常に難解な計算が必要になるため、私たちは結果を知ることができれば問題ありません。
また帰無仮説では、2つの群に差がないと仮定します。母平均に差がない場合、\(μ_1-μ_2=0\)になります。そのため対応のないt検定では、以下の公式を導き出すことができます。
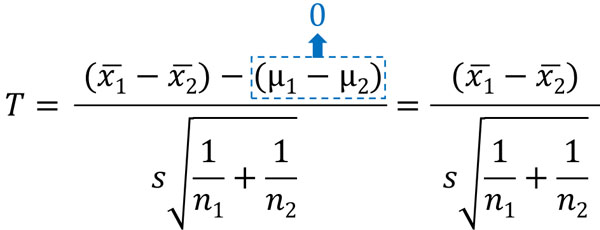
この公式を利用することによって、対応のないt分布の統計量Tを計算しましょう。
なおt検定では95%信頼区間(または99%信頼区間)を利用します。そこで有意水準として0.05(または0.01)を利用するとき、対応のない二標本t検定での自由度は\(n_1+n_2-2\)となります。
t検定をするとき、一標本t検定でも対応のある二標本t検定でも、自由度\(n-1\)のt分布を利用します。一方で対応のない二標本t検定では、2つの標本に含まれるサンプルを利用することになります。そのため自由度\(n_1-1\)と自由度\(n_2-1\)を足し、自由度\(n_1+n_2-2\)のt分布を活用するのです。
独立二群での分散(標準偏差)の計算方法
t検定をするとき、標本分散では不偏分散を利用します。つまりサンプル数から1を引いた値を利用して標本分散を計算します。
このとき標本Aと標本Bの分散を考慮する必要があるため、分散の計算は少し複雑になります。具体的には、以下の公式を利用します。
- \(s^2=\displaystyle\frac{(n_1-1)(s_1)^2+(n_2-1)(s_2)^2}{n_1+n_2-2}\)
なぜこの公式になるのかについても詳しい説明は省きます。標本Aと標本Bの分散を組み合わせる場合、この公式になると理解できれば問題ありません。
p値と帰無仮説・対立仮説を用いた検定の手順
それでは、実際に帰無仮説・対立仮説を利用して、対応のない二標本t検定をしてみましょう。以下の問題の答えは何でしょうか。
- 数学のテストを実施しました。AクラスとBクラスの点数が以下のとき、AクラスとBクラスに学力差はあるでしょうか。
| Aクラス | Bクラス |
| 50 | 70 |
| 48 | 62 |
| 40 | 55 |
| 38 | 65 |
| 66 | 52 |
| 58 | 68 |
データは正規分布し、等分散である場合、スチューデントのt検定を利用することができます。このとき、帰無仮説と対立仮説を以下のように設定しましょう。
- 帰無仮説:AクラスとBクラスに差はない
- 対立仮説:AクラスとBクラスに差がある
まず、それぞれの標本についてサンプル数\(n\)、標本平均\(\overline{X}\)、分散(不偏分散)\(s^2\)、標準偏差(不偏標準偏差)\(s\)を計算しましょう。それぞれ以下のようになります。
| Aクラス | Bクラス | |
| サンプル数\(n\) | 6 | 6 |
| 標本平均\(\overline{X}\) | 50 | 62 |
| 分散(不偏分散)\(s^2\) | 113.6 | 51.6 |
| 標準偏差(不偏標準偏差)\(s\) | 10.66 | 7.18 |
2つの標本について、分散を組み合わせましょう。公式に当てはめると以下のようになります。
\(s^2=\displaystyle\frac{(n_1-1)(s_1)^2+(n_2-1)(s_2)^2}{n_1+n_2-2}\)
\(s^2=\displaystyle\frac{5×113.6+5×51.6}{6+6-2}\)
\(s^2=82.6\)
\(s≒9.09\)
次に、統計量Tを計算しましょう。
\(T=\displaystyle\frac{\overline{x}_1-\overline{x}_2}{s\sqrt{\displaystyle\frac{1}{n_1}+\displaystyle\frac{1}{n_2}}}\)
\(T=\displaystyle\frac{50-62}{9.09×\sqrt{\displaystyle\frac{1}{6}+\displaystyle\frac{1}{6}}}\)
\(T≒-2.287\)
このとき、t分布での自由度は\((6+6-2=)10\)です。自由度10のとき、有意水準0.05(5%)は2.228です。そのため\(-2.228≦T≦2.228\)であれば、偶然起こった事象と考えることができます。ただ統計量Tは-2.287であるため、この結果は5%以下の確率で起こる稀な結果であり、偶然に起こったと考えることはできません。そのため帰無仮説を棄却し、対立仮説を採用します。
つまり、AクラスとBクラスには数学の学力に差があると判断できます。こうして、対応のない二標本t検定を利用することができます。
t検定の種類を理解し、統計を用いた検定を行う
統計学で最も利用される手法がt検定です。母集団が正規分布する場合、少数サンプルを利用することによってt分布を描くことができます。そこでt分布を利用し、t検定をすることで差があるかどうかを確認するのです。
ただt検定にはいくつかの種類があります。一標本t検定、対応のある二標本t検定、対応のない二標本t検定ではそれぞれ公式や計算方法が異なります。そこでt検定の種類や特徴を理解し、正しくt検定を利用できるようになりましょう。
またスチューデントのt検定を行う場合、正規分布していることに加えて、等分散である必要があります。そのため、事前のF検定が必要になります。
t検定を学ぶとき、多くの公式が教科書に載っています。ただ公式を覚えるよりも、t検定を行えるほうが重要です。そこで、どのようにt検定をすればいいのか理解しましょう。






