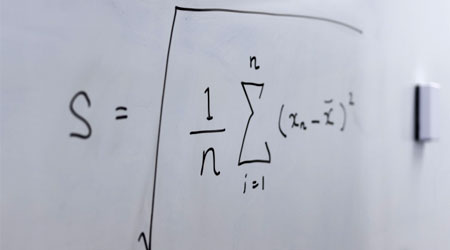統計学で学ぶ分野の一つが回帰直線です。データを集めて散布図に表した後、一つの直線を引くのです。これにより、図が何を意味しているのか理解しやすくなります。
ただ回帰直線を引くとき、ルールがあります。最小二乗法を利用することによって回帰直線を引くのが一般的です。
なお回帰直線を得たとしても、その回帰直線が意味ないケースは多いです。そこで、回帰直線が有意であるかどうか(意味あるかどうか)を検定しましょう。これにより、表計算ソフトを利用して得た回帰直線が有効かどうかを判断できるようになります。
単回帰分析をするとき、どのように利用すればいいのか理解しましょう。ここでは、回帰直線の計算方法や有効性の検定法を解説していきます。
もくじ
回帰直線として、散布図に一本の線を引く
相関係数を利用することによって、相関があるかどうかを確認できます。ただ相関の強さがわかったとしても、実世界で利用することはできません。
一方で回帰直線を利用すれば、将来の結果を予想できるようになります。例えば、売上と広告費について以下の関係があるとします。
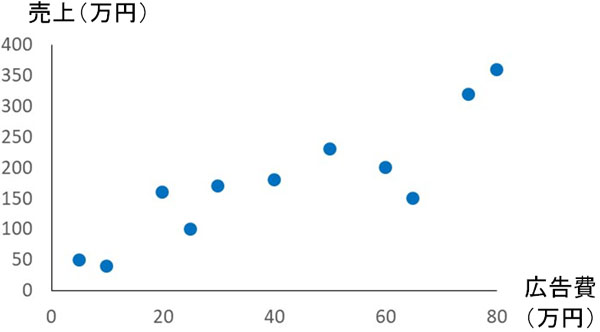
散布図を確認すると、右肩上がりであることを理解できます。つまり、広告費を使うほど売り上げが伸びるというわけです。
それでは、具体的にいくらの広告費を使えば、売り上げがどれくらいになるのでしょうか。これを予測可能にするのが回帰直線です。データを利用し、グラフ上に一本の直線(回帰直線)を引くのです。
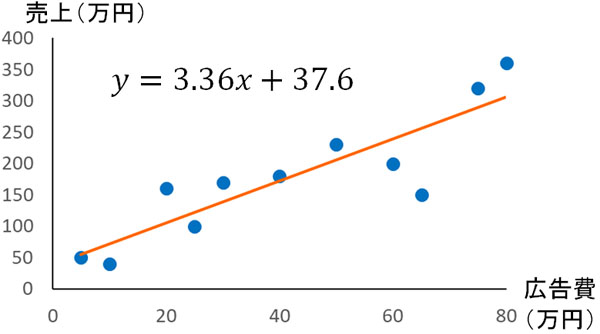
なお、回帰直線を利用して分析することを回帰分析といいます。単回帰分析では要因を横軸、結果をタテ軸に置くのが一般的です。先ほどの例であれば、要因(支払った広告費)を横軸にして、結果(売上)をタテ軸にするのです。
傾き(回帰係数)と切片を得れば回帰直線を引ける
回帰直線を引くとき、\(y=ax+b\)の式を得ることができます。一次関数のグラフになるため、当然ながら式は\(y=ax+b\)になるというわけです。
\(a\)は傾き(回帰係数)であり、\(b\)は切片を表します。単回帰分析をするとき、直線の式を求めましょう。実際の計算は表計算ソフトが行うものの、いずれにしても式を得るのです。
こうして回帰直線の式を得ることができれば、未来の予測が可能です。先ほど記したグラフでの回帰直線の式を以下に記します。
\(y=3.36x+37.6\)
散布図のグラフを確認すると、200万円の広告費を利用する場合の売上データがありません。ただこの式に\(x=200\)を代入することで、どれくらいの売上を得られるのか予想できます。
\(y=3.36×200+37.6=709.6\)
こうして、200万円の広告費によって709.6万円の売り上げを作れると予測することができます。
最小二乗法:平均値と残差を利用し、最小になる直線を描く
それでは、どのように回帰直線を引けばいいのでしょうか。ルールがない場合、誰が回帰直線を引くのかによって回帰直線の式が変わります。当然、誰が利用したとしても同じ式にならなければ統計データとして利用できません。
そこで回帰直線を引くとき、統計学では最小二乗法という方法を利用します。最小二乗法では、すべての点について、点と線の距離が最小になるように調節します。
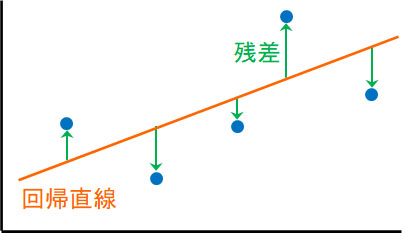
回帰直線上の値は平均値となります。そこで、回帰直線(予想の式:データの平均値)と実際の測定値の差を求めましょう。
線(回帰直線)と点(実際のデータ)の距離を残差といいます。ただ、残差はプラスになることがあれば、マイナスになることもあります。そこで残差を二乗しましょう。その後、残差の二乗の和が最小値になるように回帰直線を引きます。これにより、同じデータを利用する場合、誰が計算したとしても同じ回帰直線になります。
公式を利用し、回帰直線を引く
それでは表計算ソフトを利用するのではなく、計算によって回帰直線を引く場合はどのようにすればいいのでしょうか。先ほど解説した通り、回帰直線と実際のデータの差を求める必要があります。そのため、以下のように残差を計算します。
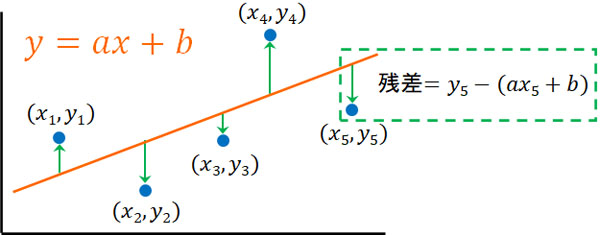
例えば5番目の点と回帰直線の残差を計算する場合、\(y_5\)から\(ax_5+b\)を引くことになります。その後、二乗しましょう。
\((y_5-ax_5-b)^2\)
また、すべての点について回帰直線との差を計算し、二乗した後に足すことになります。そのため、以下の式になります。
\((y_1-ax_1-b)^2\)\(+(y_2-ax_2-b)^2\)\(+(y_3-ax_3-b)^2…\)
\(=\displaystyle\sum{(y_i-ax_i-b)^2}\)
この式について、最小値を得られる\(a\)と\(b\)を計算すれば回帰直線の傾きと切片を求めることができます。説明を省きますが、傾き\(a\)と切片\(b\)は以下の式で計算できます。
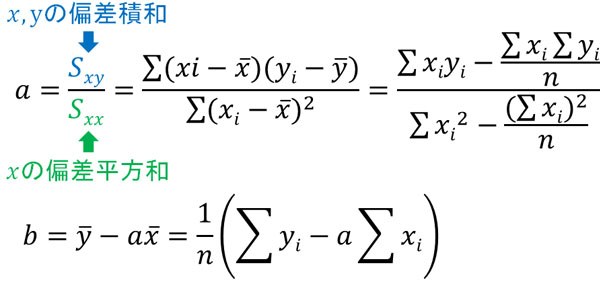
回帰直線の傾き(回帰係数)や切片を出す公式を求めるためには微分を利用しなければいけません。そのため、なぜこの公式を得られるのか詳しく理解したい場合、微分を学んだあと、\(\displaystyle\sum{(y_i-ax_i-b)^2}\)が最小になる式を導き出しましょう。そうすると、先ほどの公式を得られます。
基本的には表計算ソフトが回帰直線を計算してくれます。一方、自ら計算するときはこれらの公式を利用することによって傾き\(a\)と切片\(b\)を出し、回帰直線の式を求めましょう。
t分布を利用し、回帰係数の有意性を検定する
ただ、すべてのデータについて回帰直線を引くことができます。当然、データによっては回帰直線の信頼性が低いケースはよくあります。相関がまったくない場合、回帰直線を引いても将来の予測はできません。
そこで、回帰直線を信用できるかどうか判断できるようになりましょう。回帰係数の検定をすることによって、回帰直線の式の信頼用(回帰係数の有意性)がわかるようになります。
それでは、どのようにして回帰の有意性の検定をすればいいのでしょうか。この方法として、傾き\(a\)に着目しましょう。例えば先ほど記した「広告費と売り上げのデータ」について、相関がない場合、傾き\(a\)は0です。つまり、どれだけ広告費を出しても売り上げは上昇しません。
これはつまり、\(x\)と\(y\)に相関がないことを意味します。統計学では、差があるかどうかを証明するためには帰無仮説(差がない仮説)を利用します。つまり、「\(x\)と\(y\)には相関がない(傾きが0)」ことを帰無仮説にします。
もし帰無仮説を棄却することができれば、対立仮説(差がある)を採用します。つまり、\(x\)と\(y\)には相関があり、回帰直線の式を信頼できると判断できます。
・t分布を利用して検定を行う
回帰係数の有意性を調べるとき、利用するのはt分布です。そこで傾き\(a\)の標準誤差(データのばらつき)を利用し、統計量Tを出しましょう。95%信頼区間でのt値と計算した統計量Tを比べ、有意水準よりもp値が大きい場合、帰無仮説を棄却できます。
このときサンプル数\(n\)、\(x\)の偏差平方和\(S_{xx}\)、\(x,y\)の偏差積和\(S_{xy}\)、\(y\)の偏差平方和\(S_{yy}\)を利用すると、\(a\)の標準誤差\(S_a\)は以下の公式によって計算できます。
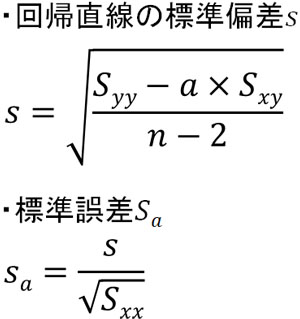
数学者が考えてくれた公式であり、意味を理解しなくてもいいので、私たちはありがたくこの公式を使わせてもらいましょう。
なお傾き(回帰係数)\(a\)の偏り度を出すため、\(a\)を\(s_a\)で割って標準化し、統計量Tを出しましょう。
- \(T=\displaystyle\frac{a}{s_a}=\displaystyle\frac{b×\sqrt{S_{xx}}}{s}\)
この統計量Tは自由度\(n-2\)のt分布に従います。そこで有意水準0.05(または0.01)となるt値と比較し、有意差があるかどうかを確認しましょう。
回帰直線の式を求め、回帰の有意性の検定を行う
それでは実際に回帰直線の式を計算によって求め、回帰の有意性の検定をしてみましょう。通常、これらの計算は表計算ソフトがしてくれます。そのため、計算できなくても基本的には問題ありません。ただ計算過程を理解すれば、どのような理論で式を出しているのかわかります。
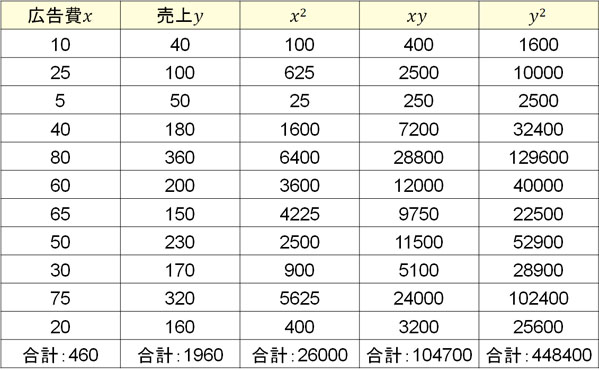
そこで以下の「広告費と売上の表」について回帰直線の式を求め、回帰係数の有意性を検定しましょう。
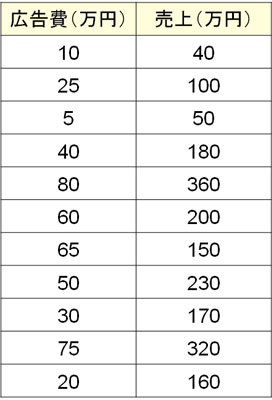
そこで以下の表を作り、\(x\)の偏差平方和\(S_{xx}\)、\(x,y\)の偏差積和\(S_{xy}\)、\(y\)の偏差平方和\(S_{yy}\)を計算しましょう。なお、サンプル数\(n\)は11です。
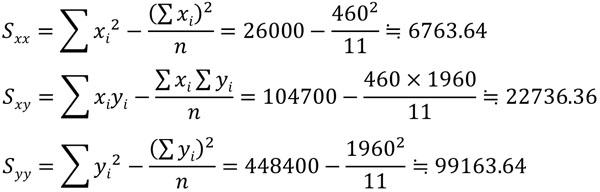
計算した値を公式に代入することによって\(S_{xx}\)、\(S_{xy}\)、\(S_{yy}\)を得ることができます。次に傾き\(a\)と切片\(b\)を計算すると以下のようになります。
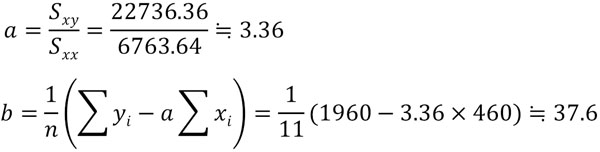
これにより、回帰直線の式は\(y=3.36x+37.6\)になるとわかります。
・回帰の有意性の検定
それでは、この回帰直線が有効かどうかを確認しましょう。帰無仮説と対立仮説は以下になります。
- 帰無仮説:\(x\)と\(y\)に相関はない(傾き\(a\)は0)
- 対立仮説:\(x\)と\(y\)に相関がある
そこで、統計量Tを求めましょう。先ほどの公式に値を代入すると以下のようになります。
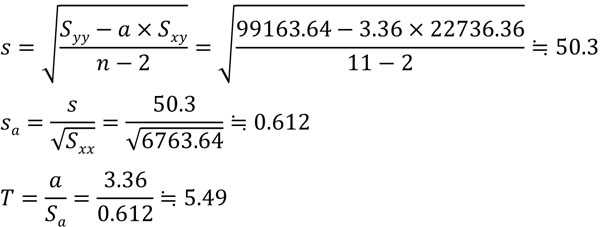
ここまで、公式に値を代入することで統計量Tを得ることができました。それでは、計算によって得られた統計量Tを有意水準と比べましょう。
前述の通り、回帰の有意性の検定では自由度\(n-2\)のt分布に従います。サンプル数は11であるため、自由度は\(11-2=9\)です。そこで自由度9のとき、有意水準0.05(5%)となるt値を統計学の教科書で確認すると2.262とわかります。
つまり統計量Tが2.262よりも大きい場合、5%以下の稀なイベントが起こっていると判断できます。p値と有意水準を比較すると、先ほど計算した統計量Tは5.49です。そのため5%以下で発生する稀なイベントが起こっているため、帰無仮説を棄却しましょう。
そこで対立仮説を採用し、\(x\)と\(y\)には相関があると判断できます。つまり今回の場合、広告費と売上の関係を表す回帰直線を利用してマーケティング戦略を練るのは意味があります。
回帰直線を利用し、将来の結果を予測する
統計で重要な分野の一つが回帰直線です。実際のデータを利用することにより、一本の線を引くことができます。回帰直線を利用することによって、将来の結果を予測できるのです。
ただ、自由に直線を引いてはいけません。回帰直線の式を得るときはルールがあり、残差の二乗をすべて足すとき、最小の値にする必要があります。この方法を最小二乗法といいます。最小二乗法を利用すれば、誰が計算しても同じ回帰直線の式を得られます。
なお、すべての散布図で回帰直線を引くことができます。そのため、得られた回帰直線が有効なのかどうかを確かめましょう。そこで、回帰の有意性の検定をしましょう。帰無仮説を棄却できる場合、「\(x\)と\(y\)に相関がある」と判断できます。
回帰直線を利用するとき、通常は表計算ソフトを利用します。ただどのように回帰直線の式を得ることができ、優位性の検定をすればいいのか学べば、より回帰直線の性質を理解できるようになります。