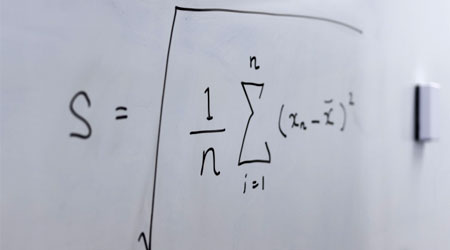母集団が正規分布しているとわかっている場合、それに基づいて統計処理をします。一方で母集団が正規分布しているかどうか不明なケースもあります。この場合、母集団の分布に関係なく利用できる統計処理をしなければいけません。これをノンパラメトリック検定といいます。
ノンパラメトリック検定には複数の種類があります。そうしたノンパラメトリック検定として、符号検定とウィルコクソンの符号順位検定があります。
符号検定では、符号がプラスなのかマイナスなのかに着目します。一方でウィルコクソンの符号順位検定では、符号に加えて「データが0からどれだけ離れているのか」を確認します。こうして統計処理をすることにより、データに差があるかどうかを判断するのです。
符号検定やウィルコクソンの符号順位検定を学べば、世の中のデータが意味あるのかどうか判断できるようになります。そこで、どのように符号検定やウィルコクソンの符号順位検定を行えばいいのか理解しましょう。
もくじ
プラスとマイナスの数に差があるかを調べるのが符号検定
ウィルコクソンの符号順位検定を理解するためには、先に符号検定を学ばなければいけません。そこでまず、概念が簡単な符号検定が何なのかについて解説していきます。
二択を利用した、非常に単純な検定方法が符号検定です。プラスとマイナスの数を調べ、差があるかどうかを調べるのが符号検定となります。例えばブドウとリンゴについて好きな果物のアンケートを取り、ブドウ好きの人が70%だったとします。この場合、偶然なのかそれとも統計学的に差があるのかを調べるのが符号検定です。
それでは「ブドウ好きが70%、リンゴ好きが30%」と判明したとき、検定できるかというと、この情報だけでは判断できません。まず、何人にアンケートを取ったのかわかりません。
符号検定では、サンプル数によって検定方法を変えます。具体的には以下のように考えましょう。
- 小標本(サンプル数が25以下):二項分布を利用して確率を計算
- 大標本(サンプル数が25超):標準正規分布を利用して確率を計算
サンプル数が少ない場合、二項分布を利用して確率の計算をするにしても手間ではありません。そのため、発生する確率を直接計算しましょう。
一方で多くの人にアンケートを取った場合、サンプル数が多くなります。その場合は確率の計算が大変になるため、標準正規分布を利用します。近似的に正規分布することを利用して確率の計算をするのです。
小標本の場合、二項分布で確率を計算する
それでは、実際に符号検定をしてみましょう。アンケートを取り、差があるかどうかを確かめてみるのです。例えば、以下の場合は差があるといえるでしょうか。
- 料理Aと料理Bについて、おいしさを10人に評価してもらいました。1~5で評価してもらい、以下の結果のとき、料理Aと料理Bに差はあるでしょうか。
| 料理A | 料理B | 符号 |
| 5 | 3 | + |
| 3 | 5 | – |
| 4 | 3 | + |
| 3 | 5 | – |
| 4 | 2 | + |
| 3 | 3 | 0 |
| 3 | 2 | + |
| 4 | 1 | + |
| 5 | 3 | + |
| 4 | 4 | 0 |
10人のうち、6人は料理Aのほうがおいしいと答えています。ただ、この結果は偶然かもしれません。そこで偶然かどうかを確かめるため、符号検定をするのです。まず、以下のように帰無仮説と対立仮説を立てましょう。
- 帰無仮説:料理Aと料理Bに差はない
- 対立仮説:料理Aと料理Bに差がある
符号検定では0を省きます。つまり、プラスまたはマイナスだけに着目しましょう。この場合、以下のようになります。
- プラス:6
- マイナス:2
なお符号検定では、数の少ないほうに着目しましょう。今回はマイナスのほうが少ないため、マイナスに着目しましょう。
より具体的には、8回中2回のマイナスが出るのは偶然なのか、それとも偶然でないのか確認しましょう。プラスとマイナスというのは、要は二択になります。二択の場合、二項分布を利用して確率を計算することができます。二項分布では、「特定のケースが出る確率またはより極端なケースが出る確率」を求めます。
今回のケースでは、以下の確率を計算した後にすべて足しましょう。
- 8回のうち、マイナスが0回出る確率
- 8回のうち、マイナスが1回出る確率
- 8回のうち、マイナスが2回出る確率
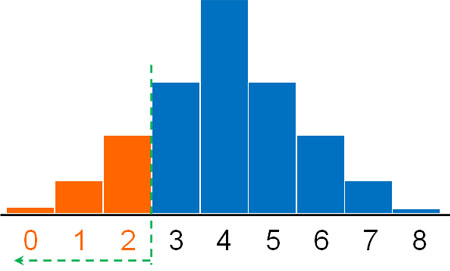
帰無仮説の場合、差がないのでプラスまたはマイナスが出る確率は\(\displaystyle\frac{1}{2}\)です。そのため、計算式は以下のようになります。
\(P=_8C_0\left(\displaystyle\frac{1}{2}\right)^0\left(\displaystyle\frac{1}{2}\right)^8\)\(+_8C_1\left(\displaystyle\frac{1}{2}\right)^1\left(\displaystyle\frac{1}{2}\right)^7\)\(+_8C_2\left(\displaystyle\frac{1}{2}\right)^2\left(\displaystyle\frac{1}{2}\right)^6\)
\(P≒0.144\)
こうして、今回の結果が出る確率は0.144(14.4%)であることがわかりました。また料理Aと料理Bに差があるかどうかの確認であるため、片側検定ではなく両側検定になります。料理Aと料理Bに差があるかどうかの確認では、プラスが多くなるケースも含める必要があるからです。参考までに、ほとんどの場合は両側検定です。
そこで両側検定にするため、0.144を2倍すると0.288(28.8%)になります。つまり今回のような結果を得られる確率は両側検定だと28.8%です。
有意水準を0.05(5%)とすると、今回の結果は0.288(28.8%)の確率で発生するため、偶然起こった結果と考えることができます。そのため帰無仮説を棄却できず、「料理Aと料理Bに差があるとはいえない」と結論付けることができます。
大標本では平均値と標準偏差を計算し、標準正規分布を利用して確率を得る
一方でサンプル数が多い場合はどのように符号検定をすればいいのでしょうか。この場合、標準正規分布を利用しましょう。
前述の通り、サンプルから0を除外します。そのためプラスの数とマイナスの数を足して25を超えるとき、標準正規分布を用いて確率を計算しましょう。また二択であるため、データ数を\(n\)とすると、帰無仮説での平均値\(μ\)は以下のようになります。
- \(μ=\displaystyle\frac{n}{2}\)
また符号分布では、以下の公式によって標準偏差\(σ\)を計算できるとわかっているのでこれを使いましょう。
- \(σ=\displaystyle\frac{\sqrt{n}}{2}\)
データ数\(n\)が多い場合、近似的に正規分布に従います。正規分布を利用して確率を出すためには、標準正規分布を利用しなければいけません。そこで、標準正規分布の確率変数\(Z\)を得る公式を使いましょう。
- \(Z=\displaystyle\frac{X-μ}{σ}\)
ただ正規分布は連続型確率分布です。例えば体重だと60kgピッタリではなく、60.1kgや59.9kgがあるように、連続している分布を作れる場合は連続型確率分布です。ただ二項分布は離散型確率分布です。プラスとマイナスの場合、分布は連続しておらず、本来のグラフはギザギザとなります。
そこで離散型確率分布を連続型確率分布に変換するときに補正をしましょう。これをイェーツの補正といいます。具体的には、以下のように公式に0.5を加えます。
- \(Z=\displaystyle\frac{X+0.5-μ}{σ}\)
プラスまたはマイナスのうち、少ない数が\(X\)になります。これに0.5を加え、\(X+0.5\)によって計算しましょう。
それでは、実際の計算はどのようになるのでしょうか。先ほどと同じように料理Aと料理Bについて、おいしさを60人に評価してもらい、以下の結果のとき料理Aと料理Bに差はあるでしょうか。
- プラスの数:35人
- 0の数:11人
- マイナスの数:14人
0の数を省くため、データ数\(n\)は49です。そのため平均値\(μ\)は24.5であり、標準偏差\(σ\)は\(\displaystyle\frac{\sqrt{49}}{2}=3.5\)です。また少ない数を基準にするため、マイナスの数に着目すると\(X=14\)です。
またイェーツの補正を利用し、0.5を加えましょう。そのため、以下のように標準正規分布での確率変数\(Z\)を計算します。
\(Z=\displaystyle\frac{14+0.5-24.5}{3.5}≒-2.857\)
統計学の教科書を開くと、標準正規分布で\(Z=-2.857\)となるときの両側確率を調べることができます。そこでマイナスを省いて\(Z=2.857\)となる確率を確認すると、0.00438(0.438%)です。有意水準0.05(5%)や有意水準0.01(1%)よりも低く、こうした稀な事象が発生していると判断できます。
そこで帰無仮説を棄却し、対立仮説を採用します。つまり、料理Aと料理Bのおいしさに違いがあると判断できます。
対応のあるt検定に相当するノンパラメトリック検定
符号検定を学んだあと、ウィルコクソンの符号順位検定を理解しましょう。符号検定では前述の通り、プラスとマイナスを利用して比較します。ただこの場合、平均値からのズレを考慮していません。例えば以下のケースを考えてみましょう。
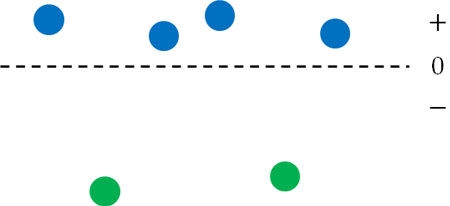
この場合、プラスのほうが数は多いです。ただ0とプラスの距離は短い一方、0とマイナスの距離は長いです。そのためプラスの数が多いとはいっても、分布がプラスとは限りません。実際の分布はマイナスかもしれません。
符号検定ではプラスとマイナスだけで判断します。ただこの場合、数字の大きさを考慮していないので正確ではありません。そこで符号に加えて、0からの距離を考慮して検定する方法がウィルコクソンの符号順位検定です。
なおウィルコクソン検定では、ウィルコクソンの符号順位検定と非常に似た名前にウィルコクソンの順位和検定があります。ただウィルコクソンの符号順位検定とウィルコクソンの順位和検定はまったくの別物なので区別しましょう。
パラメトリック検定でいう「対応のある二標本t検定」に相当するのがウィルコクソンの符号順位検定です。一方、パラメトリック検定でいう「対応のない二標本t検定」に相当するのがウィルコクソンの順位和検定です。
対応のある事象について検証し、かつ母集団が正規分布しているかどうか不明な場合、ウィルコクソンの符号順位検定を利用します。
小標本でウィルコクソン検定表を利用し、有意性を確認する
それでは、実際にウィルコクソンの符号順位検定をしてみましょう。方法としては、以下のようにして統計量Tを求めます。
- ペアについて差\(d\)を求める(差が0のケースを省く)
- 符号を無視して、小さい順に並べて順位をつける
- 少ない符号の順位を足し、統計量Tを計算する
なお順位をつけるとき、同順位の場合(例えば5と-5)の場合、順位の平均を割り当てることになります。それでは、以下の問題の答えは何でしょうか。
- パソコンにソフトウェアをインストールし、性能が向上するかどうかを点数化しました。以下の結果ではインストール前後で差はあるでしょうか。
| 前 | 後 | 差\(d\) |
| 3 | 5 | -2 |
| 16 | 8 | 8 |
| 4 | 7 | -3 |
| 4 | 4 | 0 |
| 7 | 2 | 5 |
| 10 | 3 | 7 |
| 3 | 10 | -7 |
| 7 | 2 | 5 |
| 8 | 6 | 2 |
| 5 | 7 | -2 |
まず、以下のように帰無仮説と対立仮説を立てましょう。
- 帰無仮説:インストール前後で差はない
- 対立仮説:インストール前後で差がある
差\(d\)について、符号を無視して小さい順に並べて順位をつけると以下のようになります。

次に、プラスとマイナスについて順位を並べましょう。
| プラス | 2 | 5.5 | 5.5 | 7.5 | 9 |
| マイナス | 2 | 2 | 4 | 7.5 |
マイナスのほうが少ないため、マイナスの順位を以下のようにすべて足しましょう。
\(T=2+2+4+7.5=15.5\)
差が0のデータは除くため、データ数\(n\)は\(10-1=9\)です。統計学の教科書には、データ数\(n\)に応じて、有意水準が0.05(5%)となる場合のT値がウィルコクソン検定表に掲載されています。そこでウィルコクソン検定表を利用し、データ数が9のとき、確率が0.05(5%)となる両側確率でのT値を調べると5であるとわかります。つまりT値が5よりも小さい場合、5%で起こる稀な事象が発生したと判断します。
ただ先ほどの計算では、T値は15.5です。そのため両側確率が0.05(5%)となるT値(5)に比べて数字は大きく、帰無仮説を棄却することができません。つまり偶然に起こった事象であり、ソフトウェアのインストール前後で差はないと判断できます。
なお差がある場合、少ない符号の順位を足すと、当然ながらT値は低くなります。そのため、0.05となるT値よりも、計算したT値が高ければ「差がない」と判断します。一方、0.05となるT値よりも、計算したT値が低ければ「差がある」と判断します。
大標本では標準正規分布を利用し、ウィルコクソンの符号順位検定を行う
このようにサンプル数が少ない場合、統計学の教科書に記載されているウェルコクソン検定表を利用し、有意水準が0.05(または0.01)となるT値と比較することで検定をしましょう。
一方でサンプル数が大きい場合はどのように計算すればいいのでしょうか。この場合、符号検定と同様に標準正規分布を利用して確率の計算をしましょう。サンプル数\(n\)が大きい場合、近似的に正規分布とみなすことができるからです。つまり平均値\(μ\)と標準偏差\(σ\)を利用することにより、標準正規分布を利用して確率を計算するのです。
符号検定のときとは異なる公式を利用して平均値と標準偏差を出します。細かい説明は省きますが、サンプル数\(n\)が大きい場合、以下の公式によって平均値\(μ\)と標準偏差\(σ\)を計算できることがわかっています。
- \(μ=\displaystyle\frac{n(n+1)}{4}\)
- \(σ=\sqrt{\displaystyle\frac{n(n+1)(2n+1)}{24}}\)
平均値と標準偏差を計算すれば、標準正規分布の確率変数\(Z\)を得る公式に当てはめるだけです。
- \(Z=\displaystyle\frac{T-μ}{σ}\)
符号検定とは異なり、ウィルコクソンの符号順位検定ではイェーツの補正なしに確率変数\(Z\)を計算しましょう。
例えばソフトウェアのインストールを行い、インストール前後での性能の結果が以下のとき、差はあるでしょうか。
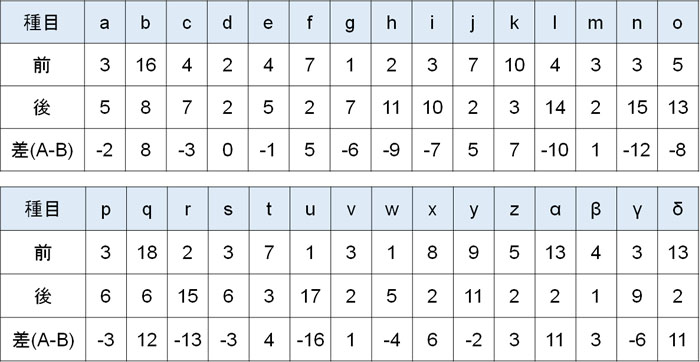
帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:インストール前後で差はない
- 対立仮説:インストール前後で差がある
そこで先ほどと同じように、順位を無視して差\(d\)を小さい順に並べましょう。その後、\(d\)の符号(プラスとマイナス)によって順位を分けましょう。差が0となるケースを省くと以下のようになります。

プラスのほうが数は少ないため、プラスの順位を足しましょう。
\(T=2+2+8+8+11.5\)\(+13.5\)\(+13.5\)\(+16\)\(+18.5\)\(+20.5\)\(+24.5\)\(+24.5\)\(+26.5\)\(=189\)
こうして、統計量Tは189になるとわかります。なお差が0のデータを省くため、データ数は\(30-1=29\)です。また平均値\(μ\)と標準偏差\(σ\)を計算すると以下のようになります。
\(μ=\displaystyle\frac{29×30}{4}=217.5\)
\(σ=\sqrt{\displaystyle\frac{29×39×59}{24}}≒52.73\)
こうして、平均値と標準偏差を求めることができました。そこで標準正規分布の確率変数\(Z\)を計算しましょう。
\(Z=\displaystyle\frac{189-217.5}{52.73}≒-0.54\)
統計学の教科書を開き、\(Z=0.54\)となる確率を確認すると0.589(58.9%)です。つまり58.9%の確率で発生する事象であり、有意水準0.05(5%)を上回っています。そのため帰無仮説を棄却できず、今回の結果は偶然に起こった事象と考えることができます。
こうして、ソフトウェアのインストール前後で性能に差はないと結論付けることができます。
符号検定とウィルコクソン検定を行えるようにする
統計学ですべての人がパラメトリック検定を学びます。t検定はパラメトリック検定です。一方で母集団が正規分布しているかどうか不明な場合、ノンパラメトリック検定を利用します。符号検定とウィルコクソンの符号順位検定はノンパラメトリック検定に分類されます。
プラスとマイナスで判断したい場合、符号検定を利用しましょう。一方で符号に加え、距離も含めた検定をしたい場合はウィルコクソンの符号順位検定を利用しましょう。
符号検定でもウィルコクソンの符号順位検定でも、サンプル数によって検定方法が異なります。ただ事象が発生する確率を求め、有意水準0.05と比べることで検定するのは同じです。
正規分布を理解している場合、符号検定とウィルコクソン検定を学べます。そこで検定法を理解し、差があるかどうかを確認できるようになりましょう。