統計学には、最尤推定法(最尤法)というやり方があります。最も一般的であろうと思われる分布を推定する方法が最尤推定法です。
ただ、知識なしに最尤推定法を学ぶと理解できません。概念は難しく、尤度関数の公式が何を意味しているのかわかりません。そこで公式の詳細を理解しましょう。
また最尤推定法(最尤法)を習うとき、多くの人が最小二乗法との違いとして何があるのか気になります。最尤推定法も最小二乗法も回帰分析でひんぱんに利用されます。そのため、両者の違いを学ぶことは重要です。
一見すると最尤推定法は難しいです。ただ実際には、原理は簡単です。そこで難しい数式を可能な限り排除し、最尤推定法の特徴を解説していきます。
もくじ
尤度とは何?世の中は最尤原理で成り立っている
統計学や機械学習を学んでいると、尤度(ゆうど)という言葉を目にすることがあります。尤度とは、一つのイベントが起こる確率を指します。
例えばコインを投げて表が2回出る確率は\(\left(\displaystyle\frac{1}{2}\right)^2\)です。つまり、尤度は\(\displaystyle\frac{1}{4}=0.25\)です。尤度というのは、確率と理解すればいいです。
また最尤原理では、「世の中で起きている現象は最も起こる確率の高いイベントが発生している」と考えます。例えば車に乗るとき、交通事故を起こす確率よりも、事故なしに目的地へたどりつく確率のほうが高いです。
私たちは常に最尤原理の中で生きています。そのため、すべての統計学は最尤原理を優先します。一般的な統計学(ネイマン・ピアソン統計学)でもベイズ統計学でも、最尤原理によって成り立っているのです。
例えば通常、一日の来店数が50人にも関わらず、ある日の来店数は200人だったとします。この場合、通常とは異なるイベントが発生していると考えます。最尤原理に基づく場合、標準偏差を10とすると、1日の来店客数は30~70人に落ち着くのが普通だからです。
そのため「店舗がマスコミ取材に取り上げられた」など、その他の要因を探すことで原因を探ります。ネイマン・ピアソン統計学やベイズ統計学を含め、最尤原理が成り立っているからこそ、特殊要因を見つけることができるのです。
最尤推定法を利用し、イカサマのコインの確率を出す
それでは、ここまで解説した原理を利用して確率を推測してみましょう。最尤推定法を利用し、イカサマのコインを探すのです。
通常、コインを投げて表になる確率は\(\displaystyle\frac{1}{2}\)です。ただイカサマのコインでは、表が出る確率は変わります。例えば以下のケースでは、イカサマのコインについて、表が出る確率はいくらでしょうか。
- コインを10回投げ、8回表が出た。
コインを投げるとき、表が出る確率について、\(\displaystyle\frac{2}{3}\)のとき、\(\displaystyle\frac{3}{4}\)のとき、\(\displaystyle\frac{4}{5}\)のとき、\(\displaystyle\frac{5}{6}\)のとき、\(\displaystyle\frac{6}{7}\)のとき、のようにさまざまなパターンで計算しましょう。
コインを10回投げ、表が8回出る確率は以下のようになります。
・表が出る確率が\(\displaystyle\frac{2}{3}\)
\(_{10}C_8\left(\displaystyle\frac{2}{3}\right)^8\left(\displaystyle\frac{1}{3}\right)^2≒0.195\)
・表が出る確率が\(\displaystyle\frac{3}{4}\)
\(_{10}C_8\left(\displaystyle\frac{3}{4}\right)^8\left(\displaystyle\frac{1}{4}\right)^2≒0.282\)
・表が出る確率が\(\displaystyle\frac{4}{5}\)
\(_{10}C_8\left(\displaystyle\frac{4}{5}\right)^8\left(\displaystyle\frac{1}{5}\right)^2≒0.302\)
・表が出る確率が\(\displaystyle\frac{5}{6}\)
\(_{10}C_8\left(\displaystyle\frac{5}{6}\right)^8\left(\displaystyle\frac{1}{6}\right)^2≒0.291\)
・表が出る確率が\(\displaystyle\frac{6}{7}\)
\(_{10}C_8\left(\displaystyle\frac{6}{7}\right)^8\left(\displaystyle\frac{1}{7}\right)^2≒0.268\)
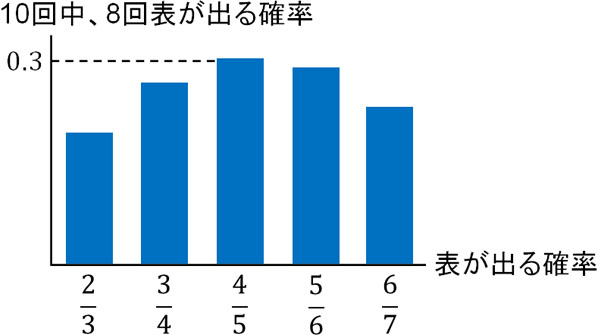
このようにさまざまなパターンで確率を計算すると、コインを一回投げて表が出る確率が\(\displaystyle\frac{4}{5}\)の場合、10回コインを投げて8回表になる確率が最も高いです。そのため今回のイカサマのコインについて、コインを一回投げて表が出る確率は\(\displaystyle\frac{4}{5}\)と推測できます。
最尤推定法については、このように「起こる確率を計算することによって最もらしい結果を採用する方法」と理解しましょう。
データを利用し、正規分布の図を描く
最尤推定法の簡単な概念を理解した後、データを利用して正規分布の図を描くことを考えましょう。最尤推定法では、母集団が正規分布に従うと仮定します。このとき最尤推定法を利用すれば、平均値\(μ\)と標準偏差\(σ\)を求めることができます。
例えば、以下のデータを得たとします。
- 2.2、3.5、5.0、5.3、6.1、6.8
このデータに最適な正規分布のグラフを描くとき、以下の2つは不適であると容易に想像できます。
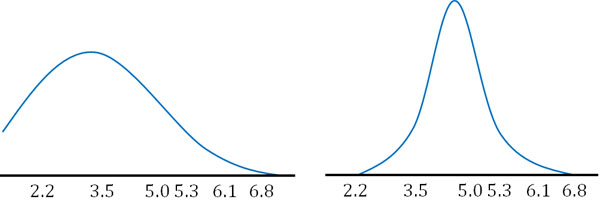
一方、以下の正規分布であれば問題なさそうに思えます。
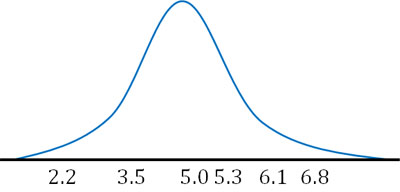
これまで説明した通り、最適な結果を得られるようにつじつまを合わせるのが最尤推定法です。
それでは、どのようなときに最適な正規分布の図を描けるようになるのでしょうか。方法としては、正規分布の確率密度関数\(f(x)\)について、それぞれの値を代入して、かけた値が最大になるようにしましょう。
つまり、以下の値が最大になるようにするのです。
\(f(2.2)\)\(×f(3.5)\)\(×f(5.0)\)\(×f(5.3)\)\(×f(6.1)\)\(×f(6.8)\)
確率密度関数\(f(x)\)を代入した値というのは、その値での確率(図での高さ)を表します。そのため、以下のように「それぞれの点での確率をすべてかけ算する」と考えましょう。
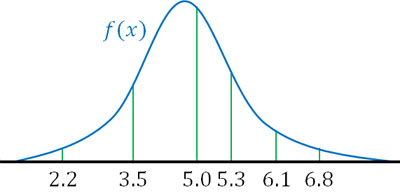
それぞれの確率は1(100%)より小さいです。最適でない正規分布のグラフでは、それぞれの確率が低くなるため、すべての確率をかけると値が小さくなります。一方で最適な正規分布のグラフだと、それぞれの確率は高くなるため、すべてかけ算することによって得られる値は最大になります。
最尤推定法と最小二乗法の違いは何か
ここまでの内容を理解すると、多くの人が疑問に思うこととして「最尤推定法と最小二乗法の違いは何か?」があります。
例えばデータから平均値\(μ\)を計算する場合、以下の違いになります。
- 最尤推定法:「サンプルデータを用いて得られる確率」が最大となる平均値を求める
- 最小二乗法:サンプルデータとの誤差が最小になる平均値を求める
最小二乗法の場合、得られたデータに対して、以下のように平均値との差(残差)が最も小さくなるように直線を引きます。
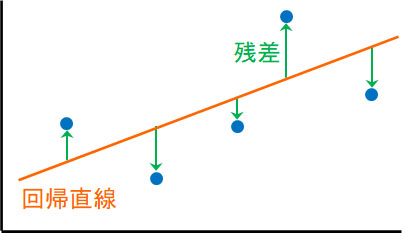
この直線を回帰直線といいます。「回帰直線上の値」と「実測値」ができるだけ小さくなるように計算することで平均値を求めます。
一方で最尤推定法では、前述の通り確率(尤度)が最大になる平均値を探します。先ほど解説した方法によって最適な正規分布のグラフを描くと、グラフの中心が平均になります。これにより、平均値を見つけることができます。
尤度関数と対数尤度関数の関係
なお最尤推定法を学ぶと、対数尤度関数を習うことになります。最尤推定法というのは、対数尤度関数の最大値を見つけることを指します。なお対数尤度関数を理解する前に、尤度関数を学びましょう。
先ほど、以下の確率密度関数\(f(x)\)が最大になる値を探すことによって、正規分布のグラフを得ることを解説しました。
\(f(2.2)\)\(×f(3.5)\)\(×f(5.0)\)\(×f(5.3)\)\(×f(6.1)\)\(×f(6.8)\)
そこで、この式を一般化しましょう。例えば、以下のデータを得たとします。
- \(x_1,x_2,x_3,…,x_n\)
この場合、以下の式になります。
- \(L=f(x_1)\)\(×f(x_2)\)\(×f(x_3)\)\(×…\)\(×f(x_n)\)
この式が尤度関数\(L\)であり、最尤推定法では\(L\)が最大になる値を探します。
なお、\(f(x)\)に代入して得た値をすべて足すときは\(\displaystyle\sum{f(x)}\)を利用します。一方、\(f(x)\)に代入して得た値をすべてかけるときは\(\displaystyle \prod f(x)\)を利用します。
\(L=f(x_1)\)\(×f(x_2)\)\(×f(x_3)\)\(×…\)\(×f(x_n)\)
\(L=\displaystyle \prod_{k=1}^n f(x_k)\)
統計学の教科書で尤度関数の公式を提示されるとき、ほとんどの人は意味を理解できないと思います。そこで、ここまで解説してきたことを学び、公式がもつ意味を理解しましょう。
なお尤度が最大になる値を見つけるとき、尤度関数ではなく、対数尤度関数を利用します。尤度関数\(L\)に対して、対数を加えただけなので概念は難しくないです。
なぜ対数を利用するかというと、計算をするときに容易になるからです。最大値を見つけるとき、微分をしなければいけません。ただかけ算の微分は式が複雑になります。そこで対数を利用すれば、かけ算を足し算に直すことができます。
\(logA×B=logA+logB\)
つまり、尤度関数\(L\)は以下のようになります。
\(logL=logf(x_1)\)\(+logf(x_2)\)\(+logf(x_3)\)\(+…\)\(+logf(x_n)\)
\(logL=\displaystyle\sum_{k=1}^{n}{logf(x_k)}\)
こうして、対数尤度関数を得ることができました。実際に微分をして極限を求める計算については、計算が複雑になるので省きます。いずれにしても、\(logL\)に対して微分すれば平均値\(μ\)や分散\(σ^2\)、標準偏差\(σ\)を得られるようになります。
なお対数尤度関数の値が最大になるとき、平均値\(μ\)と分散\(σ^2\)は以下のようになります。
- \(μ=\displaystyle\frac{x_1+x_2+…+x_3}{n}\)
- \(σ^2=\displaystyle\frac{(x_1-μ)^2+….+(x_n-μ)^2}{n}\)
※\(n\)はデータ数
つまり対数尤度関数の値が最大になるとき、\(μ\)は\(x_1,x_2,…,x_n\)の平均です。また、\(σ^2\)は\(x_1,x_2,…,x_n\)の分散です。こうして、最尤推定法を利用することによって最もらしい結果を得ることができます。
データを利用して正規分布のグラフを描くとき、最尤推定法を利用するのであれば、先ほどの結果より、全データの平均値を中心にしましょう。また分散と標準偏差を求めることにより、グラフの横幅を決めるといいです。
最尤推定法を利用し、最適な正規分布のグラフを描く
統計学の教科書では、多くの場合で公式が提示されます。ただ公式をみても内容を理解することはできません。そこで、公式がもつ意味を学びましょう。
最尤推定法というのは、最もらしい結果を推測する方法です。そこで、すべての確率をかけることによって、値が最大となる平均値や標準偏差を見つけましょう。これにより、データを利用して正規分布のグラフを描けるようになります。
また最尤推定法を学ぶとき、尤度関数を習います。公式は難しいものの、すべての確率密度関数をかけていることを理解すれば、尤度関数の公式が何を意味しているのか把握できるようになります。また尤度関数に対して対数を利用することで対数尤度関数に変換されます。対数尤度関数が最大になるように計算しましょう。
こうして最尤推定法を利用すれば、平均値や分散、標準偏差を得られます。これらの値は最もらしい結果であるため、正規分布のグラフを描くときに最尤推定法を利用するのは最適です。これらの内容を把握し、最尤推定法の概念を理解しましょう。






