緩衝液：中和によって緩衝液や塩の水溶液のpHを計算する手順

通常、酸や塩基を加えるとpHが急激に動きます。特に中性付近では、pHの変動幅が非常に大きいです。

ただ場合によっては、pHによる変動が起こってほしくない場面があります。そうしたときに利用されるのが緩衝液です。酸や塩基を加えても、pHの上昇や下落がほとんど起こらない溶液が緩衝液です。

それでは、なぜ緩衝液を利用するとpHの変動がほとんど起こらないのでしょうか。どのように緩衝液を作ればいいのでしょうか。また緩衝液を学ぶとき、不完全な中和滴定をしたり、塩のpHを計算したりする場面もあります。

これらの計算をするためには、電離定数を利用しなければいけません。そこで緩衝液の性質やpHの計算方法を解説していきます。

緩衝液の役割：pHの変化をゆるやかにする

電離平衡を学んだ後、必ず理解しなければいけないのが緩衝液です。酸または塩基を加えると、水溶液のpHは大きく変化します。ただ、この例外として緩衝液があります。緩衝液を利用する場合、強酸や強塩基を加えてもpHの変化はほとんど起こりません。

pHの変化がほとんどないため、pHを一定に保ちたい場合に緩衝液が用いられます。例えば血液や細胞内液は緩衝液で満たされています。酸や塩基によって急激にpHが変化すると、細胞に障害を与えてしまいます。そのため、pHが変化しないように血液や細胞内は緩衝液を利用しているのです。

それでは、どのように緩衝液を作るのでしょうか。以下の溶液が緩衝液の例になります。

• 弱酸 ＋ 弱酸の塩（例：CH₃COOH ＋ CH₃COONa）
• 弱塩基 ＋ 弱塩基の塩（例：NH₃ ＋ NH₄Cl）

緩衝液を理解するため、酢酸（CH₃COOH）と酢酸ナトリウム（CH₃COONa）が混ざっている例で考えましょう。酢酸は電離度が低く、水溶液には大量の酢酸（CH₃COOH）が存在します。

またナトリウムは強塩基由来の金属であるため、水溶液中で100%電離しています。つまり酢酸ナトリウム（CH₃COONa）を溶かす場合、すべて電離してCH₃COO^–とNa⁺に分かれます。そのため、水溶液中には大量のCH₃COO^–が存在します。

この緩衝液に対して、強酸として塩酸（HCl）を加えるとどうなるでしょうか。前述の通り水溶液中には大量のCH₃COO^–が存在するため、H⁺と反応することで酢酸が生まれます。また、同時に塩化ナトリウムが生まれます。

• CH₃COONa ＋ HCl → CH₃COOH ＋ NaCl

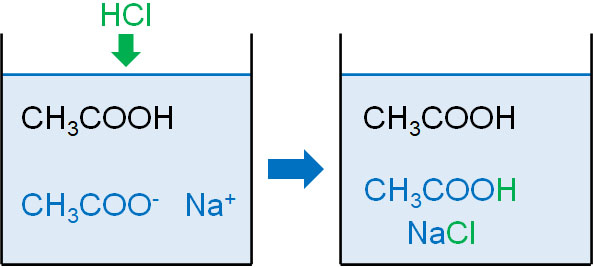
酢酸の電離度は弱いため、酢酸が生成してもpHの上昇はほとんどありません。そのため、pHの急激な上昇を防ぐことができます。

一方、強塩基として水酸化ナトリウム（NaOH）を加える場合はどうでしょうか。水溶液中には大量の酢酸（CH₃COOH）が溶けているため、水酸化ナトリウムは酢酸と反応します。

• CH₃COOH ＋ NaOH → CH₃COONa ＋ H₂O

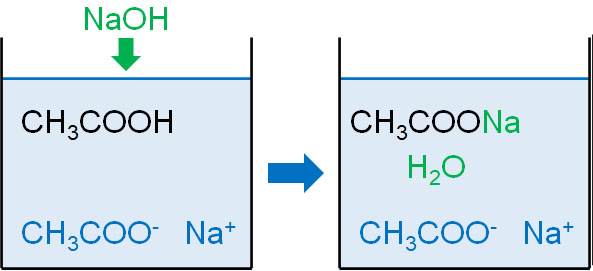
酢酸ナトリウムが生成しても、pHへの影響はほとんどありません。そのため、pHの変化を抑えることができます。

電離定数を利用し、緩衝液のpHを計算する

それでは、電離定数を利用することによって緩衝液のpHを計算してみましょう。以下の問題の答えは何でしょうか。

• 0.20mol/Lの酢酸50mLと0.20mol/Lの酢酸ナトリウム水溶液50mLを混ぜ、水を加えることで1Lにしました。電離定数K_aが2.7×10^-5mol/L、log₁₀2.7が0.43の場合、水溶液のpHを計算しましょう。なお、pHは有効数字2ケタで求めましょう。

電離定数K_aは以下の公式によって得ることができます。

• \(K_a=\displaystyle\frac{[CH_3COO^-][H^+]}{[CH_3COOH]}\)

つまり酢酸（CH₃COOH）と酢酸ナトリウム（CH₃COONa）のモル濃度がわかれば、H⁺のモル濃度を得ることができます。

なお前述の通り、酢酸の電離度は非常に低く、水溶液中でほとんど酢酸のまま存在しています。そのため酢酸イオンへの寄与は低く、「加えた酢酸の量≒水溶液中の酢酸濃度」とみなしましょう。一方、酢酸ナトリウムは水溶液中で100%電離しているため、加えた酢酸ナトリウムの量に着目しましょう。

そうすると、酢酸と酢酸ナトリウムの物質量は以下のようになります。

• 酢酸：\(0.20×\displaystyle\frac{50}{1000}=0.010\)
• 酢酸ナトリウム：\(0.20×\displaystyle\frac{50}{1000}=0.010\)

こうして、それぞれ0.010molが溶液中に溶けているとわかります。なお溶液の量は1Lなので、両方とも0.010mol/Lです。そこで電離定数K_aを利用し、H⁺のモル濃度を計算しましょう。

\(2.7×10^{-5}=\displaystyle\frac{0.01[H^+]}{0.01}\)

\([H^+]=2.7×10^{-5}\)

こうして、H⁺のモル濃度は2.7×10^-5mol/Lとわかります。そこでpHを得る公式に代入しましょう。

\(pH=-log_{10}(2.7×10^{-5})\)

\(=5-0.43\)

\(=4.57(≒4.6)\)

こうして、pHは4.6とわかります。

緩衝液に強酸または強塩基を加えるとき、変化するpHを求める

それでは、緩衝液を利用する場合は本当にpHの変化がほとんどないのでしょうか。実際に計算してみましょう。

pHが4.6の場合、強酸をわずかでも入れるとpHは1～2になります。また少しの強塩基を入れると、pHは12～13になります。ただ緩衝液に強酸または強塩基を入れる場合、pHの変化がほとんどないのです。例として、以下の問題を解いてみましょう。

• 先ほどの例題で上げた水溶液（pH=4.6）について、0.20mol/Lの水酸化ナトリウム水溶液を10mL入れる場合、pHはいくらになるでしょうか。なお電離定数Kaは2.7×10^-5mol/L、log₁₀1.8は0.26です。また、pHは有効数字2ケタで計算しましょう。

NaOHを加える場合、酢酸と反応することで酢酸ナトリウムが発生します。

• CH₃COOH ＋ NaOH → CH₃COONa ＋ H₂O

加える水酸化ナトリウムの物質量は0.0020molです。

\(0.2×\displaystyle\frac{10}{1000}=0.002\)

先ほど計算した通り、溶液中には酢酸が0.010mol、酢酸ナトリウムが0.010mol溶けています。このとき水酸化ナトリウムを0.0020mol加えると、消費される酢酸は0.0020molです。そのため、酢酸の物質量は0.0080molになります。一方で酢酸ナトリウムは0.0020mol増えます。

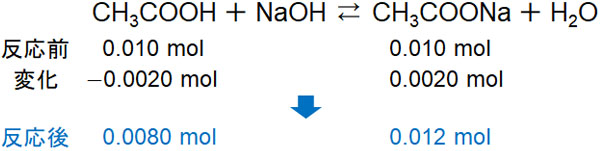
そのため反応後、酢酸の物質量は0.0080molであり、酢酸ナトリウムの物質量は0.012molになります。

また1Lの水溶液に対して10mLの水酸化ナトリウム水溶液を加えているため、全体の体積は1010mL（1.01L）です。そのため、酢酸と酢酸ナトリウムのモル濃度は以下のようになります。

• 酢酸：\(\displaystyle\frac{0.0080}{1.01}\)mol/L
• 酢酸ナトリウム：\(\displaystyle\frac{0.012}{1.01}\)mol/L

そこで電離定数K_aを利用し、H⁺のモル濃度を計算しましょう。

\(2.7×10^{-5}=\displaystyle\frac{\displaystyle\frac{0.012[H^+]}{1.01}}{\displaystyle\frac{0.0080}{1.01}}\)

\(2.7×10^{-5}=\displaystyle\frac{0.012[H^+]}{0.0080}\)

\([H^+]=\displaystyle\frac{2.7×10^{-5}×0.0080}{0.012}\)

\([H^+]=1.8×10^{-5}\)

[H⁺]のモル濃度がわかったため、pHを得る公式に代入しましょう。

\(pH=-log_{10}(1.8×10^{-5})\)

\(=5-0.26\)

\(=4.74(≒4.7)\)

このように、多めの水酸化ナトリウム水溶液を加えてもpHの変化は4.6から4.7です。緩衝液を利用すれば、計算によってもpHの変化がほとんどないとわかります。

不完全な中和反応によって生じる緩衝液のpHの計算

なお、緩衝液は中和反応によって作ることもできます。ここまで、酢酸と酢酸ナトリウムを混合する場面で解説してきました。そこで酢酸と酢酸ナトリウムを加えるのではなく、中和反応によって緩衝液を作りましょう。

例えば酢酸に水酸化ナトリウムを加える場合、以下の反応が起こります。

• CH₃COOH ＋ NaOH → CH₃COONa ＋ H₂O

酢酸と同じ物質量の水酸化ナトリウムを加える場合、水溶液に酢酸がなくなってしまいます。そこで酢酸よりも少ない物質量の水酸化ナトリウムを加えます。そうすると、溶液中に酢酸と酢酸ナトリウムの両方が存在することになります。

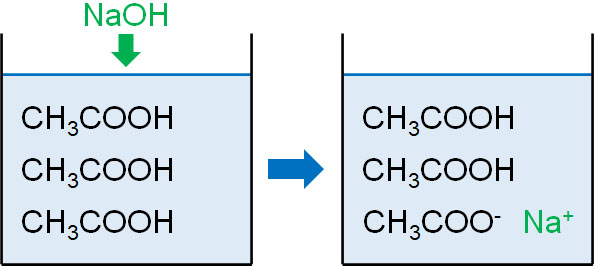
このように、不完全な中和反応によっても緩衝液を作れることを理解しましょう。また、pHの計算を行えるようになりましょう。例えば、以下の問題の答えは何でしょうか。

• 0.10mol/Lの酢酸水溶液30mLに対して、0.10mol/Lの水酸化ナトリウム水溶液を20mL加えました。溶液のpHを有効数字2ケタで求めましょう。なお電離定数Kaは2.7×10^-5mol/L、log₁₀1.35は0.13です。

まず、酢酸と水酸化ナトリウムの物質量を計算すると以下のようになります。

• 酢酸：\(0.10×\displaystyle\frac{30}{1000}=0.0030\)mol
• 水酸化ナトリウム：\(0.10×\displaystyle\frac{20}{1000}=0.0020\)mol

酢酸と水酸化ナトリウムは1：1で反応するため、反応後の物質量は以下のようになります。

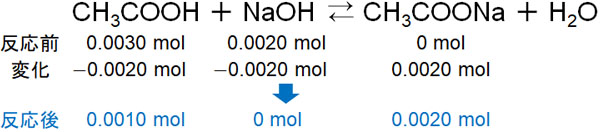
また水溶液の体積は合計で50mL（0.05L）です。そのため、酢酸と酢酸ナトリウムのモル濃度は以下のようになります。

• 酢酸：\(\displaystyle\frac{0.001}{0.05}\)mol/L
• 酢酸ナトリウム：\(\displaystyle\frac{0.002}{0.05}\)mol/L

そこで電離定数K_aを利用し、H⁺のモル濃度を計算しましょう。

\(2.7×10^{-5}=\displaystyle\frac{\displaystyle\frac{0.002[H^+]}{0.05}}{\displaystyle\frac{0.001}{0.05}}\)

\(2.7×10^{-5}=\displaystyle\frac{0.002[H^+]}{0.001}\)

\([H^+]=\displaystyle\frac{2.7×10^{-5}×0.001}{0.002}\)

\([H^+]=1.35×10^{-5}\)

[H⁺]のモル濃度を計算した後、pHを得る公式に代入しましょう。

\(pH=-log_{10}(1.35×10^{-5})\)

\(pH=5-0.13\)

\(pH=4.87(≒4.9)\)

こうして、pHは4.9であるとわかりました。これまで解説した方法と同じように、反応後の酢酸と酢酸ナトリウムのモル濃度を計算し、電離定数の公式に当てはめることで答えを得ることができます。

電離定数を利用し、塩の水溶液のpHを求める

先ほど、不完全な中和反応を利用してpHの計算をしました。それでは、すべての酢酸を中和させて反応を完了させる場合はどのようにpHの計算をすればいいのでしょうか。

酸と塩基を混ぜると塩（えん）が生成されます。塩によっては酸性を示したり、塩基性を示したりすることを既に習っていると思います。復習すると以下のようになります。

それでは、弱酸性を示す塩や弱塩基性を示す塩について、pHはいくらになるのでしょうか。塩の水溶液のpHを求められるようになりましょう。

計算方法については、手順を理解する必要があります。塩のpHを計算するときは記号を省いたり、逆数を利用したりしなければいけません。つまり、計算方法を覚えていないとほとんどの人は問題を解けません。基本的な計算方法は同じであるものの、塩のpHを得るにはコツがあるのです。

そこで、完全に中和させることによって得られる塩のpHを計算してみましょう。例えば、以下の問題の答えは何でしょうか。

• 0.10mol/Lの酢酸水溶液100mLに対して、0.10mol/Lの水酸化ナトリウム水溶液を100mL加えました。溶液のpHを求めましょう。なお酢酸の電離定数K_aは2.0×10^-5mol/L、log₁₀2は0.30、水のイオン積[H⁺][OH^–]は1.0×10^-14(mol/L)²です。

まず、中和後に起こっている平衡状態を記載しましょう。酢酸は弱酸であり、水酸化ナトリウムは強塩基です。そのため、生成する塩は弱塩基の性質を示します。

Na⁺は強塩基由来であるため、水溶液中ですべて電離しています。同時に、中和反応によって生じる酢酸イオンについても、水溶液中ですべてCH₃COO^–で存在します。ただ、中性の水溶液中に酢酸ナトリウム（CH₃COONa）が存在する場合、以下の反応によって水溶液は塩基性を示すようになります。

• CH₃COO^– ＋ H₂O ⇆ CH₃COOH ＋ OH^–

そこで酢酸ナトリウムのモル濃度と電離定数K_aに着目して問題を解きましょう。

・生成する酢酸ナトリウムの物質量を計算する

酢酸ナトリウムの物質量がわからないと計算できません。そこで、中和反応によって生まれる酢酸ナトリウムの量を計算しましょう。

酢酸と水酸化ナトリウムは1：1で中和反応を起こします。0.10mol/Lの酢酸水溶液100mLと0.10mol/Lの水酸化ナトリウム水溶液100mLを加えているため、生成する酢酸ナトリウムの物質量は以下のようになります。

\(0.10×\displaystyle\frac{100}{1000}=0.010\)

こうして、生成する酢酸ナトリウムの物質量は0.010molとわかりました。

・酢酸イオンから、酢酸と水酸化物イオンが生成物する物質量を計算する

次に、酢酸イオンが水と反応することで酢酸と水酸化物イオンへ変化するとき、どれだけの物質量が生成するのか計算しましょう。生成する水酸化物イオンの物質量を\(x\)とすると、酢酸イオンと水との反応後は以下のようになるとわかります。

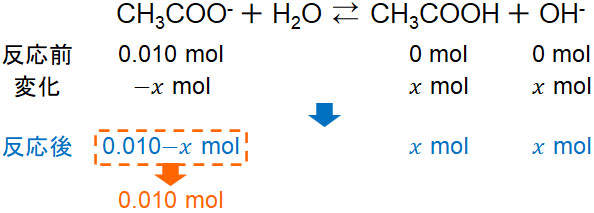
電離平衡の計算では、水溶液には大量の水が存在するため、水の量はほとんど変化がなく、平衡に寄与しないので削除できることは既に習っていると思います。そこで、水が関与する反応は無視しましょう。

またもう一つ重要なのは、反応後に生成するCH₃COO^–の物質量を\(0.010-x\)molではなく、0.010molにすることです。本来、反応後の物質量は\(0.010-x\)molが正しいです。それにも関わらず、なぜ\(x\)を排除してもいいのでしょうか。

前述の通り、弱酸や弱塩基の電離度は値が非常に低いです。0.010molに比べて値が非常に小さい場合、誤差として取り扱うことができます。数学の計算であれば、\(0.010-x\)を0.010にしてはいけません。ただ化学では、有効数字の概念があることからわかる通り、非常に小さい数字は省けるのです。

・物質量をモル濃度に直す

それでは先ほどの結果を利用して、物質量をモル濃度に直しましょう。酢酸と水酸化ナトリウムをそれぞれ100mL加えているため、合計は200mL（0.2L）です。そのため、モル濃度は以下のようになります。

• 酢酸イオン：\(\displaystyle\frac{0.010}{0.2}=0.05\)mol/L
• 酢酸：\(\displaystyle\frac{x}{0.2}=5x\)mol/L
• 水酸化物イオン：\(\displaystyle\frac{x}{0.2}=5x\)mol/L

そこで、電離定数を利用して水酸化物イオンのモル濃度を得ましょう。ここでは、酢酸イオンの電離定数をK_hとします。K_hは以下のように表されます。

• CH₃COO^– ＋ H₂O ⇆ CH₃COOH ＋ OH^–
• \(K_h=\displaystyle\frac{[CH_3COOH][OH^-]}{[CH_3COO^-]}\)

※前述の通り、電離平衡では[H₂O]を省きます。

・K_hの逆数を利用し、水のイオン積をかける

ただ、酢酸イオンの電離定数K_hは問題文に与えられていません。私たちがわかるのは、酢酸の電離定数K_a（2.0×10^-5mol/L）です。どのようにして、K_hを得ればいいのでしょうか。

まず、酢酸の電離定数を記しましょう。以下のようになります。

• CH₃COOH ⇆ CH₃COO^– ＋ H⁺
• \(K_a=\displaystyle\frac{[CH_3COO^-][H^+]}{[CH_3COOH]}\)

次に、K_aの逆数を取ります。なぜ逆数を取るのか疑問に思ってはいけません。ひとまず、逆数にすると以下のようになります。

\(\displaystyle\frac{1}{K_a}=\displaystyle\frac{[CH_3COOH]}{[CH_3COO^-][H^+]}\)

その後、両辺に対して水のイオン積をかけましょう。pHの性質より、[H⁺]と[OH^–]をかけると1.0×10^-14(mol/L)²になります。つまり[H⁺]と[OH^–]のかけ算は定数であり、決まった一つの値になります。そのため、両辺に[H+][OH-]をかけて以下の式を作りましょう。

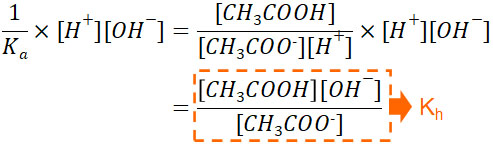
こうしてK_aの逆数と水のイオン積[H⁺][OH^–]を利用することでK_hを得ることができました。K_hや酢酸のモル濃度、水酸化物イオンのモル濃度、酢酸イオンのモル濃度はわかっているため、値を代入することによってOH^–のモル濃度を得ることができます。

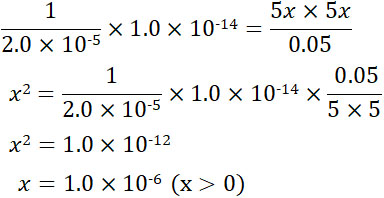
こうして、水溶液中に含まれているOH^–の物質量（\(x\)の値）は1.0×10^-6molとわかりました。1.0×10^-6molが200mL（0.2L）に溶けているため、OH^–のモル濃度は5.0×10^-6molです。

\(\displaystyle\frac{1.0×10^{-6}}{0.2}=5.0×10^{-6}\)

また前述の通り、水のイオン積は1.0×10^-14になるため、存在する[H⁺]（H⁺のモル濃度）は以下のようになります。

\(1.0×10^{-14}=5.0×10^{-6}×[H^+]\)

\([H^+]=2.0×10^{-9}\)

そこで、pHを得る公式に当てはめましょう。

\(pH=-log_{10}(2.0×10^{-9})\)

\(pH=9-0.30\)

\(pH=8.7\)

こうして、塩の水溶液のpHを求めることができました。緩衝液や電離定数に関わる問題の中でも、塩のpHを計算するときは手順を覚える必要があり、計算の過程は複雑です。ただ物質量やモル濃度、電離定数を利用することによって[H⁺]を出し、pHを計算するのは同じです。

電離定数を利用し、緩衝液のpHの計算を行う

化学を学ぶとき、難しい内容の一つが電離平衡です。その中でも、緩衝液は問題の内容が複雑になりやすいです。

ただ、基本的な解き方は同じです。物質量やモル濃度を計算した後、電離定数を利用してpHを計算しましょう。

なお場合によっては、解き方を覚えていないと答えを得られないケースがあります。代表例が塩のpHの計算です。不完全な中和であれば緩衝液を作れます。一方で完全な中和では塩によって水溶液は酸性または塩基性になります。このとき、pHを計算できるようになりましょう。

化学の計算問題というのは、解き方を理解しているかどうかが重要です。特に電離平衡の計算では、弱酸（または弱塩基）の物質量を無視するなど、解き方を覚えていないと計算が難しいです。そこで、どのように電離定数を利用して計算すればいいのか理解しましょう。