イオン結晶の結晶格子と共有結合の結晶：CsCl型、NaCl型、ZnCl型

イオンが固体として析出するとき、結晶を作ります。イオンはイオン結合によってつながっており、イオン結晶には種類があります。

イオン結晶では、結晶中に複数の原子が存在することになります。金属結晶のように、一つの原子だけで構成されているわけではありません。そのため金属結晶に比べて、イオン結晶は内容が複雑になります。

またイオン結晶では主に3つの種類があります。それぞれの結晶について、イオンの総数やイオン半径を解答できるようにならなければいけません。なお、これらイオン結合の結晶を学べば、共有結合の結晶についても理解できるようになります。

事前に結晶の形を覚えておく必要があり、さらにはイオン結晶では計算問題も出されます。そこで、イオン結晶の特徴や半径の計算方法、共有結合の結晶について解説していきます。

1 イオン結晶で重要な体心立方格子と面心立方格子
- 1.1 イオン結晶の種類：CsCl型、NaCl型、ZnCl型
2 配位数や単位格子に含まれるイオンの総数、イオン半径と単位格子の長さとの関係
3 共有結合の結晶はZnS型となっている
4 イオン結晶と共有結合の結晶での結晶構造

イオン結晶で重要な体心立方格子と面心立方格子

化学でイオン結晶を学ぶとき、必ず事前に金属結晶を学びましょう。金属結晶は金属元素一つで構成されるため、イオン結晶に比べて構造が単純だからです。金属結晶で学んだ内容を利用すれば、イオン結晶を理解しやすくなります。

金属結晶には主に3種類の結晶格子（原子の空間的な配列）が存在し、その中に体心立方格子と面心立方格子があります。

・体心立方格子

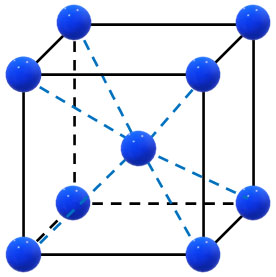
・面心立方格子（金属結晶）

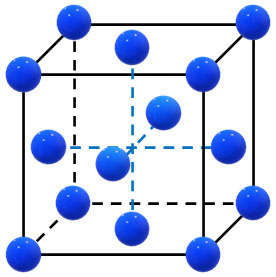
イオン結晶では、体心立方格子と面心立方格子を利用します。ただ前述の通り、イオン結晶では一つの原子で構成されているのではなく、複数の原子で構成されています。そのため、少し内容が複雑になるのです。

イオン結晶の種類：CsCl型、NaCl型、ZnCl型

それでは、イオン結晶の種類を確認しましょう。イオン結晶には主に3つの種類が存在し、それぞれの単位格子（最も小さい単位の結晶格子）は以下のようになります。

・CsCl型：体心立方格子がベース

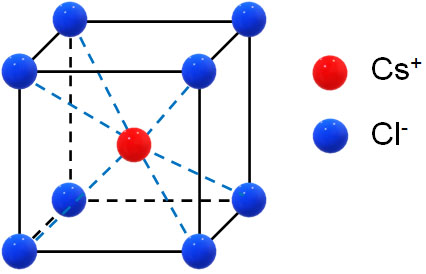
Cs⁺が中心にあり、その周辺をCl^–が取り囲んでいます。イオン結晶でのCsCl型というのは、金属結晶での体心立方格子と同じと理解しましょう。

・NaCl型：面心立方格子がベース

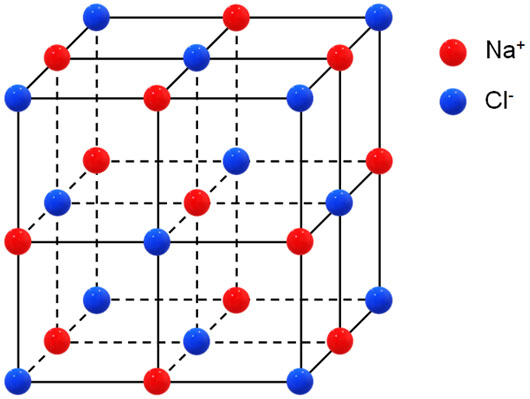
面心立方格子をベースにした結晶格子がNaCl型です。Na⁺とCl^–が交互に存在します。

・ZnS型：面心立方格子がベース

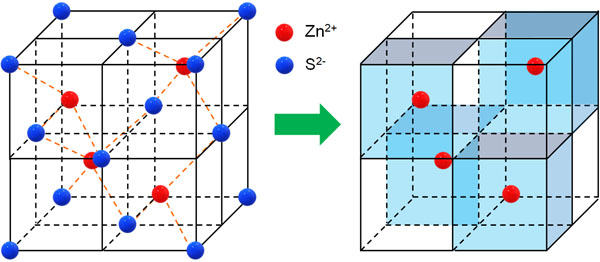
面心立方格子がベースとなっているものの、特殊な結晶格子がZnS型です。S^2-の配置は面心立方格子と同じです。その間にZn²⁺が入ることによって結晶格子が構成されています。

配位数や単位格子に含まれるイオンの総数、イオン半径と単位格子の長さとの関係

イオン結晶の結晶格子を学ぶとき、以下を答えられるようにしましょう。

配位数
単位格子に含まれるイオンの総数
イオン半径と単位格子の一辺の長さとの関係

金属結晶では、配位数（1つの原子に隣接している原子の数）や単位格子に含まれる原子の総数、原子半径を答えなければいけない問題がひんぱんに出されます。イオン結晶についても、同じ問題が出されるのです。

配位数や単位格子に含まれる原子の総数については、金属結晶もイオン結晶も考え方が同じです。一方、イオンでは2種類以上の物質を利用するため、イオン半径の計算は注意しなければいけません。

CsCl型の結晶格子は体心立方格子で考える

まず、イオン結晶で最も単純なCsCl型の結晶格子から確認していきましょう。金属結晶とほぼ同じであるため、配位数と単位格子に含まれるイオンの総数を答えるのは難しくありません。

配位数については、Cs⁺に着目すると8つのCl^–に取り囲まれていることがわかります。また1：1でイオン結合を形成しているため、Cl^–についても8つのCs⁺に取り囲まれることになります。

一方、単位格子に含まれるイオンの総数について、真ん中にCs⁺が1つあります。

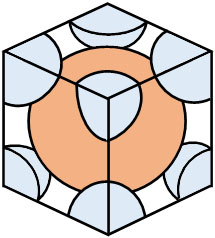
それに対してCl^–は\(\displaystyle\frac{1}{8}\)が8個あります。つまり、結晶格子にCl^–は1つあります。そのため、合計の原子の数は2です。

\(1+\displaystyle\frac{1}{8}×8=2\)

次にイオン半径と単位格子の長さとの関係を考えましょう。Cs⁺のイオン半径をr_Cs、Cl^–のイオン半径をr_Cl、結晶格子の一片の長さを\(a\)とします。このとき、以下の図を利用してイオン半径と結晶格子の一辺の長さとの関係を出しましょう。

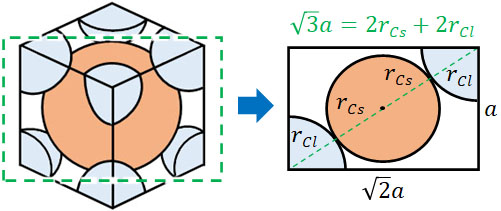
三平方の定理を利用すると、右図の対角線の長さは\(\sqrt{3}a\)です。そのため、以下の関係になるとわかります。

\(\sqrt{3}a=2r_{Cs}+2r_{Cl}\)

金属結晶の体心立方格子で原子半径を計算する方法を理解している場合、イオン半径の計算も可能です。原子の種類は2つになるものの、考え方は同じです。

NaCl型の結晶格子は面心立方格子で考える

それでは、NaCl型の結晶格子はどのように考えればいいのでしょうか。面心立方格子をベースにしているものの、NaClは2種類の原子を含むため、金属結晶とは異なる考え方をしなければいけません。

配位数を数えるとき、NaCl型の結晶格子では真ん中にある原子に着目しましょう。例えば以下の図では、真ん中にあるNa⁺に着目します。

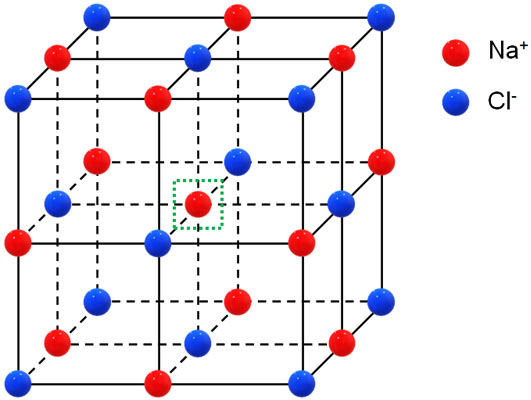
そうすると、Na⁺は6つのCl^–と接していることがわかります。そのため、Na⁺の配位数は6です。またNa⁺とCl^–は1：1の割合であるため、Cl^–の配位数は6です。

なお単位格子に含まれる原子の数について、単位格子を確認すると以下のようになります。

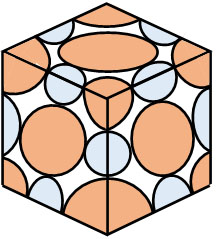
そこで辺の中心にあるイオンをNa⁺とすると、Na⁺は合計で4つあります（辺の中心にそれぞれ\(\displaystyle\frac{1}{4}\)、単位格子の中心に1つ）。

\(\displaystyle\frac{1}{4}×12+1=4\)

一方、Cl^–（オレンジ色）は4つあるとわかります。

\(\displaystyle\frac{1}{2}×6+\displaystyle\frac{1}{8}×8=4\)

そのため、NaCl型の結晶格子には合計で8つの原子が存在します。

次に、イオン半径と単位格子の一辺の長さとの関係を計算しましょう。以下の図を作ることによって計算できます。

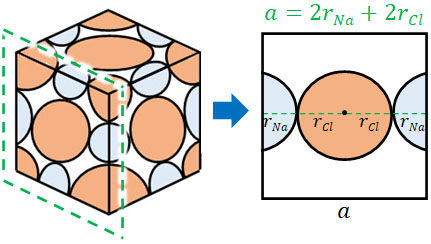
Na⁺のイオン半径をr_Na、Cl^–のイオン半径をr_Cl、結晶格子の一片の長さを\(a\)とします。この場合、イオン半径と単位格子の長さとの関係は以下のようになります。

\(a=2r_{Na}+2r_{Cl}\)

金属結晶での単位格子に比べて、イオン結晶では配位数の考え方が異なります。また単位格子に含まれるイオンの数やイオン半径の計算方法も異なります。そこで、どのような結晶構造になっているのか理解しましょう。

ZnS型の結晶格子は特殊な面心立方格子

イオン結晶で難しい概念がZnS型です。S²⁺に着目すると、面心立方格子と同じ配置になっていることがわかります。一方でZn²⁺では、立方体の中心に1つ飛ばしで原子が入っています。

そこで、Zn²⁺に着目しましょう。以下のように単位格子の一部を取り出すと、Zn²⁺の周囲には4つのS²⁺が存在するとわかります。

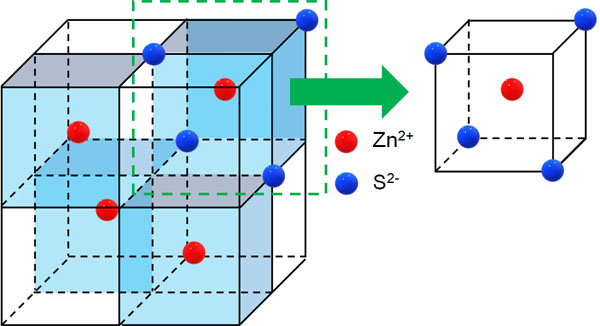
こうして、Zn²⁺の配位数は4であるとわかります。またZnSは1：1の割合でイオンを作るため、S²⁺の配位数も4です。

また単位格子に存在する原子数を確認しましょう。Zn²⁺は立方体の中心に存在します。単位格子を確認すると、立方体の数は4つなので、Zn²⁺の数は4であることがすぐにわかります。またS²⁺はZn²⁺と1：1の割合で結合しているため、単位格子に存在するZn²⁺は4とわかります。そのため、単位格子に存在する合計の原子は8つです。

次にイオン半径と単位格子の一辺の長さとの関係を計算しましょう。Zn²⁺のイオン半径をr_Zn、S^2-のイオン半径をr_S、結晶格子の一片の長さを\(a\)とします。このとき単位格子の一部を取り出すと、イオン半径と単位格子の一辺の長さとの関係は以下のようになります。

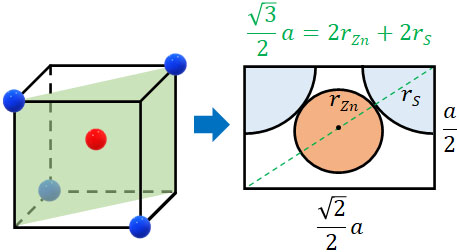
単位格子の一辺の長さは\(a\)であるため、右図のたての長さは\(\displaystyle\frac{a}{2}\)です。そのため三平方の定理を利用して横の長さを計算すると\(\displaystyle\frac{\sqrt{2}a}{2}\)になります。つまり、図の対角線の長さは\(\displaystyle\frac{\sqrt{3}a}{2}\)です。

また\(r_{Zn}+r_S\)によって、対角線の半分の長さを出すことができます。そのため、以下の関係が成り立ちます。

\(\displaystyle\frac{\sqrt{3}a}{2}=2r_{Zn}+2r_S\)

こうして、イオン半径と単位格子の一辺の長さとの関係を表すことができました。

共有結合の結晶はZnS型となっている

ここまでの内容を理解したら、次に共有結合の結晶を学びましょう。なぜイオン結晶の後に共有結合の結晶を学ぶのがいいかというと、共有結合の結晶はZnS型となっているからです。共有結合の結晶としては、炭素（C）やケイ素（Si）が有名です。

共有結合の結晶の中でも、黒鉛（C）は層状の構造をしています。それに対して、ダイヤモンド（C）やケイ素（Si）、二酸化ケイ素（SiO₂）、炭化ケイ素（SiC）は正四面体構造をしています。言い換えると、ダイヤモンド（C）やケイ素（Si）、二酸化ケイ素（SiO₂）はZnS型の構造になっているのです。

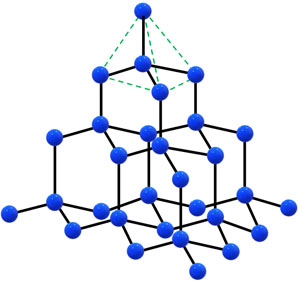
先ほどZnS型の結晶について、配位数や単位格子に含まれるイオンの総数、半径と単位格子の一辺の長さとの関係を解説してきました。共有結合の結晶の場合、イオンは存在しません。そこでイオンを「共有結合を形成している原子」に置き換えましょう。そうすると、共有結合の結晶について単位格子に存在する原子の数や原子半径を計算できるようになります。

共有結合の結晶では、すべて共有結合でつながっているため硬く、融点が高いです。またイオン結晶とは違って水に溶けにくいです。ほかには、金属結晶とは違って電気を通しません（結晶構造が大きく異なる黒鉛は例外的に電気を通します）。こうした違いを理解しましょう。