統計学では多くの分布を学びます。その中でも、非常に特殊な分布の一つがコーシー分布です。特殊な分布なので重要ではないものの、物理学でコーシー分布が観測されることがあります。
コーシー分布はブライト・ウィグナー分布やローレンツ分布とも呼ばれています。そのため統計学の教科書ではなく、物理学の教科書ではブライト・ウィグナー分布やローレンツ分布で記されることもあります。
一般的な確率分布とは異なり、コーシー分布には期待値や分散が存在しません。これが、コーシー分布が特殊な確率分布と認識されている理由です。
それでは、コーシー分布はどのような性質をもつ確率分布なのでしょうか。ここでは、コーシー分布の特徴を解説していきます。
もくじ
コーシー分布とは何か:期待値・分散が存在しない
通常、確率分布には期待値や分散があります。しかし前述の通り、コーシー分布には期待値や分散が存在しません。そのため、理解しにくい確率分布となっています。
コーシー分布は連続型確率分布です。また、コーシー分布は発見者のヘンドリック・ローレンツの名を取ってローレンツ分布とも呼ばれています。
特殊な確率分布であるため、多くの確率分布で利用されている法則がコーシー分布では当てはまりません。そのため、例外としてコーシー分布がひんぱんに利用されます。
正規分布(ガウス分布)に比べ、ゆるやかに減少する分布
まず、コーシー分布はどのようなグラフの形になるのでしょうか。コーシー分布では、以下のように横に幅広い連続型確率分布になります。
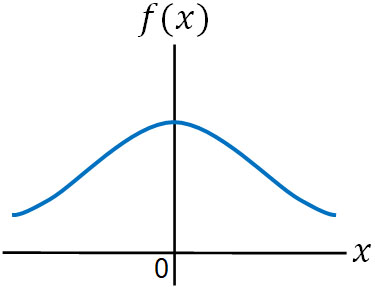
通常、確率分布では指数関数的に確率が減少していきます。例えば統計学で最も重要な正規分布(ガウス分布)であれば、以下のように標準偏差の2倍の範囲内に95.5%の確率が含まれます。標準偏差の3倍であれば、99.7%の確率が含まれます。
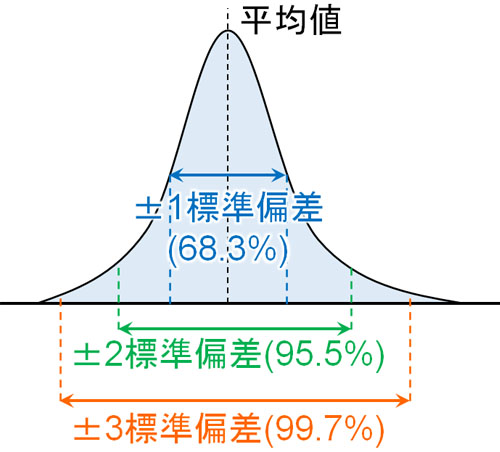
つまり、正規分布では外れ値を取る可能性が低いです。
一方でコーシー分布の場合、\(x\)の値が大きくなるとき(または小さくなるとき)、指数関数的に確率が減少していくことがありません。前述の通り、横に幅広いグラフの形となるのです。これを「裾が重い分布」といいます。
裾が重い分布であるため、コーシー分布(ブライト・ウィグナー分布、ローレンツ分布)では外れ値を取るケースが多くなります。正規分布と同じ左右対称のグラフではあるものの、確率密度の性質は大きく異なります。
大数の法則や中心極限定理はコーシー分布で成立しない
なお期待値や分散が存在しないというのは、大数の法則や中心極限定理が成立しないことを意味しています。
試行回数が多い場合、必ず期待値(平均)へと収束していくのが大数の法則です。ただ平均値がない以上、何らかの値に近づくことはないのです。
また試行回数が多い場合、平均値または合計を確認すると正規分布となります。この法則が中心極限定理です。中心極限定理によってほとんどの分布で正規分布となるため、あらゆるケースで正規分布(ガウス分布)を利用することができます。
ただ期待値が存在しないため、コーシー分布では中心極限定理が成立しません。ほとんどの分布で中心極限定理を利用できるものの、コーシー分布は中心極限定理の例外としてひんぱんに利用されます。
標準コーシー分布での確率密度関数
それでは、コーシー分布の確率密度関数はどのようになっているのでしょうか。標準コーシー分布(コーシー分布の中でも、最も一般的な分布)の場合、以下が確率密度関数\(f(x)\)になります。
- \(f(x)=\displaystyle\frac{1}{π(x^2+1)}\)\((-∞<x<∞)\)
この公式をみても理解できないと思いますが、ひとまず「この確率密度関数に値を代入すると、コーシー分布での確率密度を計算できる」と納得してください。
なお、\(\displaystyle\frac{1}{π}\)は正規化定数です。確率密度をすべて合計するとき、1(100%)になるように調節する定数が正規化定数です。合計の確率密度を1にする値が正規化定数であるため、\(π\)は以下のように計算できます。
- \(π=\displaystyle \int_{-\infty}^{\infty} \displaystyle\frac{1}{x^2+1} dx\)
いずれにしても、標準コーシー分布では定数と\(x\)を利用することによって、確率密度を計算することができます。
期待値(平均)が存在しないことの証明
それでは、なぜコーシー分布では期待値(平均)が存在しないのでしょうか。左右対称のグラフを描くため、平均値は0(中央値)と考えてしまいます。ただ、実際には異なります。つまり期待値はゼロではなく、特定の値を記すことができないのです。
そこで期待値の定義にしたがって、コーシー分布での期待値\(E(X)\)の計算をしてみましょう。以下のようになります。
\(E(X)=\displaystyle \int_{-\infty}^{\infty} xf(x) dx\)
\(=\displaystyle\frac{1}{π} \displaystyle \int_{-\infty}^{\infty} \displaystyle\frac{x}{x^2+1} dx\)
\(=\displaystyle\frac{1}{π} \displaystyle \int_{-\infty}^{0} \displaystyle\frac{x}{x^2+1} dx\)\(+\displaystyle\frac{1}{π} \displaystyle \int_{0}^{\infty} \displaystyle\frac{x}{x^2+1} dx\)
\(=∞-∞\)
無限大から無限大を引くことになるため、特定の値を定めることができません。また期待値(平均)というのは、無限大よりも値が小さい必要があります。これらの理由から、コーシー分布には期待値が存在しないのです。
また期待値が存在しないため、分散を定義することもできません。分散の計算には期待値を利用するため、これについては当然です。参考までに、分散\(V(X)\)は以下の公式を利用して計算します。
- \(V(X)=E(X^2)-E(X)^2\)
このように、分散の計算には期待値の存在が必須です。そのため、コーシー分布には期待値だけでなく分散も存在しません。
特殊な確率分布がコーシー分布
統計学では、特殊な分布としてコーシー分布を学ぶことがあります。通常、確率分布には期待値と分散があります。そのため、合計したり平均を利用したりすることによって正規分布となります。また大数の法則や中心極限定理に従います。
ただ、これらの法則に従わない例外が存在します。この例外としてひんぱんに示されるのがコーシー分布です。
外れ値を取るケースが多く、裾が重い分布となるのがコーシー分布です。グラフの形は正規分布(ガウス分布)と似ているものの、分布の特徴は大きく違うのです。
統計学や物理学でコーシー分布(ブライト・ウィグナー分布、ローレンツ分布)を学びます。そこでコーシー分布について、その他の確率分布との違いや特徴を理解しましょう。