医療統計で頻繁に利用される方法にコホート研究と症例対照研究(ケースコントロール研究)があります。コホート研究は前向き研究と呼ばれており、症例対照研究は後ろ向き研究と呼ばれます。要は将来に向かって研究をするのか、過去に向かって研究をするのかによって研究法が違ってきます。
またコホート研究の場合、相対危険度(RR)を利用して統計処理することになります。一方で症例対照研究の場合、オッズ比を利用して差があるかどうかを判定します。
臨床研究をするとき、コホート研究のほうが信頼性は高いです。ただコホート研究は時間がかかります。それに対して症例対照研究のほうが信頼性は低いものの、ビッグデータを活用して論文の量産も可能です。
それでは、コホート研究と症例対照研究にはどのような違いがあるのでしょうか。また、どのように統計処理をすればいいのでしょうか。ここではコホート研究と症例対照研究(ケースコントロール研究)の内容を解説していきます。
もくじ
医療統計で広く利用されるコホート研究と症例対照研究
臨床研究では必ずコホート研究と症例対照研究(ケースコントロール研究)を学ばなければいけません。論文を読むにしても、医療論文では多くのケースでコホート研究または症例対照研究をしていることになります。
このとき、コホート研究と症例対照研究には以下の違いがあります。
- コホート研究(前向き研究):未来に向かって研究を行う
- 症例対照研究(後ろ向き研究):過去に向かって研究を行う
コホート研究というのは、原因を追究するために行います。原因があるため、何かが起こります。そこで原因を探るため、未来に何が起こるのか観察するのがコホート研究です。
一方で症例対照研究の場合、結果ありきの研究になります。既に何か悪いことが起こっている場合、どのような理由でそのような結果になったのか調査するのです。これがコホート研究と症例対照研究の違いです。
コホート研究と症例対照研究(ケースコントロール研究)の例
それでは、具体的にコホート研究と症例対照研究ではどのような研究方法の違いとなるのでしょうか。
コホート研究の場合、暴露ありと暴露なしの群を用意します。例えばタバコと肺がんの関係を知りたい場合、タバコを吸っている人と吸っていない人を調べます。当然ながら、タバコを吸っている人のみを調べても何もわかりません。
タバコを吸っていない人と比べることで、ようやく肺がんの発症確率が高くなっているのか、それとも低くなっているのかわかるのです。
また前向き研究であるコホート研究では、将来に向かって調査をします。そのため2つの群を用意した後、「調査開始日から10年間でどれくらいの人が肺がんを発症したか」を調べます。このように、コホート研究では未来に向かって調べるというわけです。
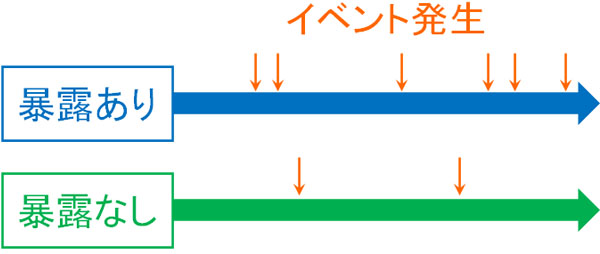
調査するとき、暴露ありの群と暴露なしの群で明らかにイベント発生数が異なる場合、病気を発症した原因を特定できます。
なお症例対照研究(ケースコントロール研究)についても、2つの群を用意して比較します。このときは病気ありと病気なしの群を利用します。ただコホート研究とは異なり、過去にさかのぼって研究をするのがケースコントロール研究です。
そこで同じ年齢の人を集め、肺がんを発症した人と発症していない人について、過去の喫煙歴を調査します。これにより過去の暴露歴を調べ、何が原因か調査するのです。
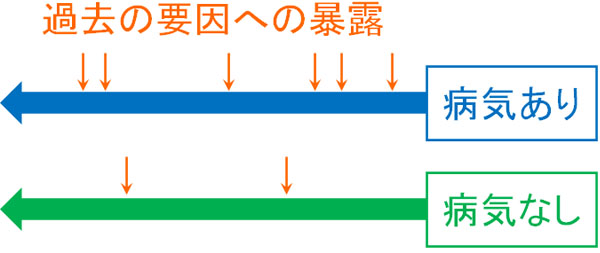
同じ臨床研究であっても、コホート研究と症例対照研究は内容が大きく異なります。
症例対照研究より、コホート研究のほうが精度は高い
当然ながら、コホート研究のほうが時間はかかります。コホート研究をする場合、5~20年という長い時間をかけての追跡調査が必要になることは多いです。当然、途中で脱落する調査対象者もたくさん現れます。そのため前向き研究であるコホート研究はかなり大変な調査方法です。
ただ大変だからこそ、ケースコントロール研究に比べ、コホート研究のほうが精度や信頼性は高いです。
また、実際のところ何が原因で病気を発症するのかわからないケースは多いです。そうしたとき、コホート研究では開始時点で原因がわからなかったとしても、研究によって原因を突き止めることも可能です。
一方、過去の事例を調べる方法であるため、コホート研究に比べて圧倒的に調査時間を削減できるのが症例対照研究です。
ただケースコントロール研究のほうが精度は低いです。調査対象となる人にアンケートを取るにしても、その回答の内容が本当に正しいかどうかわかりません。また多くの人は過去の出来事を忘れているため、コホート研究のように正確に内容を把握することができないのです。
ビッグデータなど過去の事例を利用して論文を量産したい場合、症例対照研究は最適です。ただ臨床研究の信頼性という意味では、ケースコントロール研究はコホート研究に劣ります。
コホート研究での相対危険度(RR)の公式と意味
それでは、コホート研究やケースコントロール研究を行う方法を理解しましょう。コホート研究でも症例対照研究(ケースコントロール研究)でも、以下の表を利用して統計処理をしていきます。
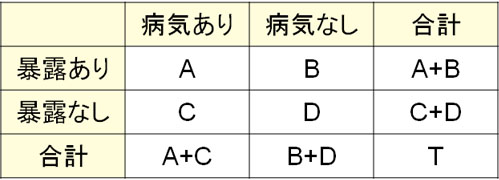
ただ、同じ表を利用するものの、統計処理の方法が異なります。まずはコホート研究について解説していきます。
すべてのコホート研究では相対危険度(RR)を利用します。相対危険度は以下の公式によって計算することができます。
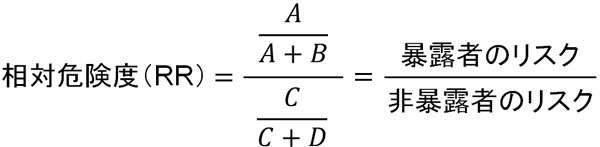
それでは、この公式は何を意味しているのでしょうか。\(A+B\)によって、要因に対して暴露ありのすべての人を足すことができます。その後、病気を発症した人(A)を割ることによって、要因暴露した人のリスク(病気発症の割合)を知ることができます。
一方で\(C+D\)をすれば、要因への非暴露者をすべて足すことができます。そこで病気を発症した人(C)を割れば、要因へ暴露していない人のリスク(病気の発症割合)を得ることができます。
もし要因暴露者でリスクが高い場合、当然ながら\(\displaystyle\frac{A}{A+B}\)の値は大きくなります。そこで暴露者のリスク(割合)と非暴露者のリスク(割合)を利用することによって、相対危険度(PR)を計算するのです。
もし要因への暴露と病気の発症に関係がない場合、相対危険度は1になります。関係ないケースだと分子と分母が同じ数字になるため、これは当然だといえます。一方で要因暴露によってリスクが増える場合、\(\displaystyle\frac{A}{A+B}\)の値が大きくなり、結果として相対危険度の値は大きくなります。
例えば相対危険度が2の場合、非暴露者に比べて、暴露者は2倍の病気発症リスクがあると判断できます。
相対危険度を利用して95%信頼区間を得る
次に相対危険度(RR)を利用して95%信頼区間を出しましょう。95%信頼区間を出すとき、標準正規分布では標準偏差を1.96倍することによって計算したと思います。また99%信頼区間の場合、標準偏差を2.58倍することによって計算しました。
同じように、相対危険度を用いて95%信頼区間を出すときについても1.96を利用しましょう(99%信頼区間の場合は2.58を利用する)。このとき相対危険度(RR)の95%信頼区間を出すため、以下の公式を利用して\(x\)を求めましょう。
\(x=ln(PR)±1.96\sqrt{\displaystyle\frac{\displaystyle\frac{B}{A}}{A+B}+\displaystyle\frac{\displaystyle\frac{D}{C}}{C+D}}\)
私たちは数学者ではなく、統計処理できればそれでいいです。そのため、公式の意味は深く考えなくていいです。
次に、計算して得た\(x\)について、\(e^x\)に代入しましょう。\(x\)は2つの値が出るため、\(e^x\)に2つの値を代入するのです。仮に\(x\)の答えが\(a\)と\(b\)のとき、以下のようになります。
- \(e^a<e^x<e^b\)
このとき、\(e^a<e^x<e^b\)の範囲に1を含んでいない場合、「暴露群と非暴露群で差がある」ことになります。
コホート研究での統計処理の例
それでは、先ほど解説した公式を利用して実際に計算してみましょう。例えば、以下のコホート研究を実施したとします。
- 遺伝子Xがあるかどうかを幼児のときに調べ、20年後に肥満であったかどうかを調査したら以下の結果を得られました。遺伝子Xと肥満は関係あるでしょうか。
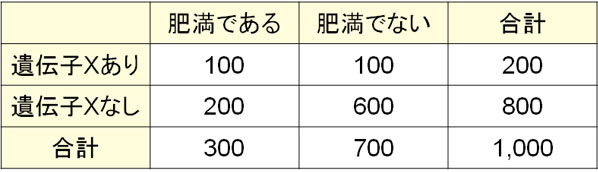
未来に向かって調査している研究であるため、コホート研究になります。また、20年後にイベント発症の有無(肥満かどうか)を調べるという非常に簡単な内容のコホート研究になります。
それでは、実際に計算をしてみましょう。まずは相対危険度(RR)を求めます。
\(RR=\displaystyle\frac{100÷200}{200÷800}=2\)
RRが2であるため、遺伝子Xがあると2倍肥満になりやすいことがわかります。それでは、統計的に差があると判断できるでしょうか。95%信頼区間を利用して確認してみましょう。
相対危険度(RR)の95%信頼区間を得るため、先ほど提示した公式を利用して\(x\)を計算しましょう。
\(x=ln2±1.96\sqrt{\displaystyle\frac{100÷100}{200}+\displaystyle\frac{600÷200}{800}}\)
\(x≒0.510,0.876\)
こうして、\(x=0.510\)と\(x=0.876\)を得ることができました。次に\(e^{0.510}\)と\(e^{0.876}\)を計算しましょう。
\(e^{0.510}≒1.665\)
\(e^{0.876}≒2.401\)
そのため、\(1.665<e^x<2.401\)となります。95%信頼区間に1を含んでいないため、今回の結果は「遺伝子Xと肥満は関係がある」と解釈できます。
ケースコントロール研究で利用されるオッズ比
次に症例対照研究(ケースコントロール研究)での統計方法を学びましょう。症例対照研究の場合、オッズ比(OR)を利用することで計算します。オッズ比では、名前の通り比を利用します。
それでは、症例対照研究ではなぜオッズ比を利用するのでしょうか。この理由として、コホート研究とは異なり、症例対照研究では「集団の人数」を設定することができないからです。
コホート研究では最初に集団の人数を設定します。例えば先ほど、「遺伝子Xありの人:200人」「遺伝子Xなしの人:800人」と決めました。この標本は母集団を代表しており、最初に人数を設定するため、その後の調査によって罹患率を測定することができます。
一方でケースコントロール研究の場合、病気ありの人と病気なしの人は研究者が集めることになります。その後、要因暴露があったかどうかを調べます。つまり、コホート研究とは違って「要因暴露があった正確な人数(または、要因暴露がなかった人数)」を知ることができません。
「要因暴露があったかどうか」についてアンケートを取ったとしても、ケースコントロール研究では回答が正確ではありません。本人が過去の出来事を忘れている可能性は高いです。また要因暴露の有無を「遺伝子Xがあるかどうか」を基準にするにしても、20年前と現在では遺伝子の活動状況が大きく変化しており、結果が正しくないケースは多いです。
症例対照研究はあくまでも過去の調査をするため、最初の人数を決定することができません。そのため、コホート研究のように集団の人数を決定できず、公式にある\(A+B\)と\(C+D\)の正確な人数を計算することができません。
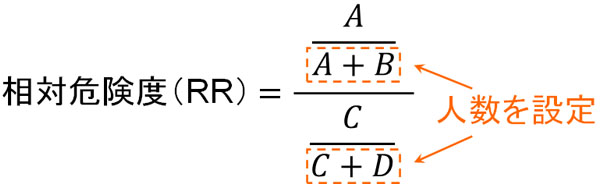
症例対照研究(ケースコントロール研究)では、罹患率を計算することはできません。最初の人数を決めることができないため、\(A+B\)や\(C+D\)の計算をしても意味がないのです。
そこでケースコントロール研究では、コホート研究とは異なる方法によって計算しなければいけません。そこでオッズ比を利用して統計処理をします。
オッズ比(OR)を計算する公式と意味
標本全体の正確な人数を出すことはできないものの、比であれば計算することができます。つまり病気ありと病気なしの人について、暴露群と非暴露群でそれぞれ比率を出すのです。
オッズ比は以下の公式によって計算することができます。

このように合計人数を利用せず、\(\displaystyle\frac{A}{B}\)を利用することで暴露者のリスク比率を計算します。また、\(\displaystyle\frac{C}{D}\)を利用して非暴露者のリスク割合を計算しましょう。
もし暴露群と病気が関係しているのであれば、\(\displaystyle\frac{A}{B}\)の値は大きくなります。つまり、オッズ比は大きい値になります。
なおオッズ比を得た後、オッズ比の95%信頼区間を計算します。95%信頼区間を出す場合、先ほどと同じように1.96を利用します(99%信頼区間の場合は2.58を利用する)。オッズ比の95%信頼区間を出すため、以下の公式を利用して\(x\)を計算します。
- \(x=ln(OR)\)\(±1.96\sqrt{\displaystyle\frac{1}{A}+\displaystyle\frac{1}{B}+\displaystyle\frac{1}{C}+\displaystyle\frac{1}{D}}\)
その後に\(x\)を利用し、\(e^x\)を計算しましょう。例えば\(x\)の答えが\(a\)と\(b\)の場合、コホート研究と同様に、以下の計算をします。
- \(e^a<e^x<e^b\)
この区間に1が含まれていない場合、暴露群と非暴露群に差があると判断できます。
オッズ比を活用し、症例対照研究での統計処理を行う
それでは、実際にオッズ比を利用して症例対照研究をしてみましょう。コホート研究で利用した先ほどの事例を活用すると以下のようになります。
- 20代の肥満の人と肥満でない人を集め、遺伝子Xが存在するかどうかを調べました。以下の結果のとき、遺伝子Xと肥満に関係はあるでしょうか。

オッズ比(OR)を出すため、公式を利用して計算しましょう。以下のようになります。
\(OR=\displaystyle\frac{100×600}{100×200}=3\)
こうして、オッズ比は3であるとわかりました。この値は有意差があるのでしょうか。有意差を確認するため、公式を利用して\(x\)を出しましょう。
\(x=ln3\)\(±1.96\sqrt{\displaystyle\frac{1}{100}+\displaystyle\frac{1}{100}+\displaystyle\frac{1}{200}+\displaystyle\frac{1}{600}}\)
\(x≒0.779,1.419\)
こうして、\(x=0.779\)と\(x=1.419\)を得ることができました。次に電卓やパソコンを使い、\(e^x\)に値を代入して計算しましょう。
\(e^{0.779}=2.179\)
\(e^{1.419}=4.133\)
こうして、\(2.179<e^x<4.133\)になるとわかりました。オッズ比の95%信頼区間に1が含まれていないため、肥満と遺伝子Xは関係しているとわかります。
症例対照研究の場合、今回のように肥満である人と肥満でない人を集めた後、調査をします。そのため本当に遺伝子Xが関係しているかどうかは不明であり、ほかの要因によって肥満になったのかもしれません。
またコホート研究であれば、何のイベントが発生したのかそのつど調査できます。例えば、年齢が低いときは体重が同じであったものの、思春期のころから群の間で体重差を確認できるようになるかもしれません。
一方で症例対照研究は自己申告になりますし、詳しい調査をすることができません。そのため、どうしてもコホート研究に比べるとバイアスが大きくなり、圧倒的に研究の精度が劣るというわけです。
医療統計ではコホート研究と症例対照研究が重要
コホート研究と症例対照研究(ケースコントロール研究)は医療統計で頻繁に利用されます。そこで、コホート研究や症例対照研究をどのように行うのか理論を理解しましょう。
研究をするとき、コホート研究のほうが圧倒的に大変です。標本を集めるだけでなく、その後の追跡調査を何年も行う必要があります。そのため労力と時間はかかるものの、精度の高い研究をすることができます。
一方で症例対照研究の場合、過去のイベント発生を調べる方法です。そのためコホート研究に比べて楽であり、ビッグデータを利用することで論文の量産も可能です。ただコホート研究よりも大幅に精度は劣ります。
こうした違いを理解して、相対危険度(RR)やオッズ比(OR)を利用して統計処理をしましょう。コホート研究と症例対照研究は医療統計で非常に重要なので、原理を知っていると論文の内容をより深く理解できるようになります。






