二者択一の結果になるケースは多く、そうした場合に利用されるのが二項分布です。一方、負の二項分布という確率分布が存在します。
負の二項分布では、失敗回数\(x\)を利用します。二項分布では成功回数のみを利用して確率を計算します。それに対して、負の二項分布では成功回数だけでなく、失敗回数を考慮して確率を計算することになります。
それでは、負の二項分布の確率関数はどのようになっているのでしょうか。また、期待値(平均)や分散はどのように計算すればいいのでしょうか。
二項分布と非常に似ているものの、新たな概念となるのが負の二項分布です。そこで、負の二項分布の特徴や公式の意味、期待値・分散の計算方法を解説していきます。
もくじ
負の二項分布とは何か?離散型確率分布での確率分布
結果が二つだけの試行をベルヌーイ試行といいます。コインを投げるとき、結果は表または裏です。またサイコロを投げるとき、結果は1の目またはそれ以外です。このような施行がベルヌーイ試行です。
ベルヌーイ試行を何度も行うことによって二項分布を得られます。同様にベルヌーイ試行を何度も行うことにより、負の二項分布を得られます。
負の二項分布では、成功確率\(p\)のイベントについて、\(k\)回成功するまでに\(x\)回の失敗をするときの確率分布を得ることができます。
ベルヌーイ試行を行うため、負の二項分布は離散型確率分布に分類されます。二項分布とほとんど同じですが、失敗回数が含まれるのが負の二項分布の特徴です。
一般的な二項分布と負の二項分布の違い
それでは、具体的に二項分布と負の二項分布でどのような違いがあるのかについて、より詳細に確認していきましょう。
サイコロを投げるとき、1の目が出たら成功、1の目以外が出たら失敗とします。1の目が出る確率は\(\displaystyle\frac{1}{6}\)です。また、1の目以外が出る確率は\(\displaystyle\frac{5}{6}\)です。それでは、サイコロを5回投げて1の目が2回出る確率はいくらでしょうか。
二項分布を理解している場合、確率は以下のようになると計算できます。
\(_5C_2\left(\displaystyle\frac{1}{6}\right)^2\left(\displaystyle\frac{5}{6}\right)^3≒0.161\)
一方で負の二項分布ではどのような計算になるのでしょうか。先ほどと同じように、サイコロを5回投げる場面を考えましょう。サイコロを投げて1の目が3回出るまでに、1の目以外が2回出る確率はいくらでしょうか。
高校数学を学んでいる場合、全員がこの問題を解くことができると思います。サイコロを投げて3回目に1の目が出るためには、以下の条件でなければいけません。
- それまでに1の目が2回出ており、かつ1の目以外が2回出ており、5回目に1の目が出る。
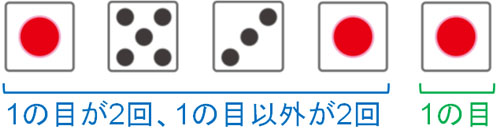
そのため、以下の計算式になります。
\(_4C_2\left(\displaystyle\frac{1}{6}\right)^2\left(\displaystyle\frac{5}{6}\right)^2×\displaystyle\frac{1}{6}≒0.0193\)
こうして\(k\)回成功(1の目が出る)までに、\(x\)回失敗する(1の目以外が出る)確率を出すことができました。
負の二項分布の確率関数
負の二項分布というのは、概念は難しくありません。\(k\)回の成功するためには、それまでに\(k-1\)回の成功をしていなければいけません。また\(k\)回の成功をするまでに\(x\)回の失敗をする場合、\(k\)回目の成功の一つ前に合計で\(k+x-1\)の試行をすることになります。そして、最後(\(k\)回目)で成功します。
つまり\(k+x-1\)回の試行の中から、\(x\)回の失敗を選ぶ必要があります。サイコロの例であると、以下のようになります。
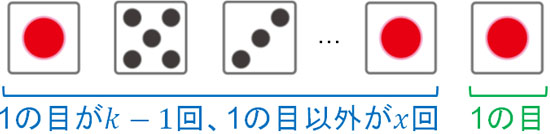
そのため成功確率が\(p\)の場合、以下の式を作ることができます。
\(_{k+x-1}C_xp^{k-1}(1-p)^x×p\)
\(=_{k+x-1}C_xp^k(1-p)^x\)
こうして、負の二項分布の確率関数を得ることができました。高校数学で学ぶ確率の初歩を理解していれば、負の二項分布の確率関数を出すことができます。
統計学の教科書で負の二項分布を学ぶ場合、最初に公式が出されます。そのため、ほとんどの人は理解できません。そこで、公式がもつ意味を学びましょう。\(k\)回成功するまでに\(k-1\)回と\(x\)回の試行をしていることを理解すれば、なぜ先ほど提示した公式を得られるのかわかります。
期待値(平均)を得る公式
次に、負の二項分布で期待値(平均)を得る公式を学びましょう。どのようにして期待値の計算をすればいいのでしょうか。
成功確率が\(p\)であり、成功回数が合計で\(k\)回の場合、負の二項分布の期待値\(E(X)\)は以下のようになります。
- \(E(X)=\displaystyle\frac{k(1-p)}{p}\)
例えばサイコロを投げて成功確率が\(\displaystyle\frac{1}{6}\)であり、合計で3回成功する場合、期待値は以下のようになります。
\(\displaystyle\frac{3\left(1-\displaystyle\frac{1}{6}\right)}{\displaystyle\frac{1}{6}}=15\)
このように、失敗回数\(x\)を利用せずに期待値を計算できます。なお、期待値の計算でなぜ先ほどの公式になるのかは解説しません。証明したい場合、期待値の定義を利用して計算してみましょう。
負の二項分布で分散を計算する
それでは、負の二項分布で分散を得るにはどのようにすればいいのでしょうか。負の二項分布で分散\(V(X)\)を出したい場合、以下の公式を利用しましょう。
- \(V(X)=\displaystyle\frac{k(1-p)}{p^2}\)
分散を得る公式は期待値を得る公式と似ています。先ほどの例題について、分散を計算すると以下のようになります。
\(\displaystyle\frac{3\left(1-\displaystyle\frac{1}{6}\right)}{\left(\displaystyle\frac{1}{6}\right)^2}=90\)
このように公式を用いて分散を計算しましょう。なお分散の公式を証明したい場合、分散の定義を利用して計算するといいです。
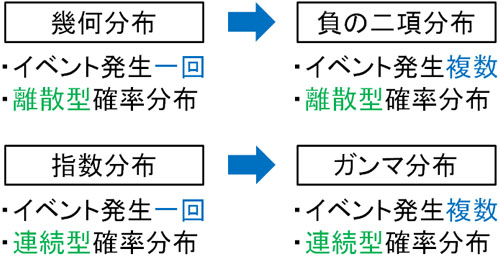
幾何分布や指数分布、ガンマ分布など、ほかの確率分布との関係
なお確率分布には、多くの種類の分布が存在します。そのため、ほかの確率分布との関係を理解にしくいです。二項分布と負の二項分布との関係は既に説明しました。ザックリと以下のようになります。
- 二項分布:試行回数を固定し、成功回数(イベントの発生回数)が確率変数となる
- 負の二項分布:成功回数(イベントの発生回数)を固定し、試行回数が確率変数となる
一方、負の二項分布は幾何分布や指数分布、幾何分布とも関係性があります。
・幾何分布との関係
負の二項分布について、\(k=1\)のときが幾何分布です。つまり、初めてイベントが発生する確率を表すのが幾何分布です。
離散型確率分布の中でも、イベント発生回数が一回の場合は幾何分布です。一方、イベント発生回数が複数の場合は負の二項分布です。
・指数分布との関係
幾何分布や負の二項分布は離散型確率分布です。一方、連続型確率分布にて、初めてイベントが発生するまでの確率を表すのが指数分布です。幾何分布について、離散型確率分布を連続型確率分布に変えると指数分布になります。
・ガンマ分布との関係
指数分布は次のイベントが一回発生するまでの確率を表します。一方、イベントが何度も発生する場合の確率を表す連続型確率分布がガンマ分布です。
言い換えると、負の二項分布(離散型確率分布)を連続型確率分布に変えるとガンマ分布になります。
統計学では多くの分布を学ぶことになります。そこで、それぞれの確率分布の特徴を理解しましょう。
負の二項分布を利用し、試行回数ごとの確率を計算する
高校数学で確率の計算を習っている場合、負の二項分布を理解するのは簡単です。合計で\(k\)回成功し、それまでに\(x\)回の失敗をするためには、\(k-1\)回目までに\(x\)回の失敗をすればいいです。これを理解すれば、負の二項分布の確率関数を得ることができます。
二項分布で成功回数(イベントの発生回数)が変動するのに対して、負の二項分布では試行回数が変わります。
また負の二項分布が何を意味しているのか理解したのであれば、期待値(平均)と分散を計算できるようになりましょう。公式を利用し、値を当てはめることによって期待値と分散を得ることができます。
統計学の教科書を読み、公式を覚えても利用できません。そうではなく公式が何を意味しているのか理解し、負の二項分布の特徴を学びましょう。






