統計学で最も重要な法則の一つが中心極限定理です。中心極限定理を理解していない場合、統計学を学んだとはいえません。それくらい重要な法則が中心極限定理です。
それでは、中心極限定理とは何なのでしょうか。中心極限定理があるからこそ、ほとんどの分布は正規分布することになります。そのため正規分布を利用することによって、簡単に確率を計算できるようになります。なぜ中心極限定理を利用するかというと、単純に便利だからです。
また中心極限定理では大数の法則が重要になりますし、「どのように正規分布を利用して確率を計算するのか」についての方法を理解しなければいけません。
統計学を学ぶとき、中心極限定理が何を意味しているのか必ず理解しましょう。そこで、中心極限定理の意味や例題を含めて解説していきます。
もくじ
理論的な確率に収束する大数の法則
中心極限定理を学ぶ前に、大数の法則を理解しましょう。大数の法則とは、「試行回数が多いと必ず理想的な確率に収束する」という法則です。
例えばコインを投げる場合、表と裏の二種類があります。表が出るのか、裏が出るのかわかりません。ただ何度もコインを投げる場合、表が出る確率は\(\displaystyle\frac{1}{2}\)に収束します。
次にサイコロを投げるとき、出る目はいくつになるでしょうか。1~6の数字について、出る確率はそれぞれ\(\displaystyle\frac{1}{6}\)です。そのためサイコロの期待値は3.5になります。
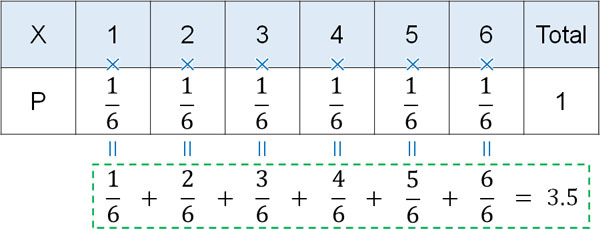
つまり何度もサイコロを投げる場合、平均値は3.5に収束していきます。このように試行回数を増やすと、期待値(理論値)に近づいていくのが大数の法則です。
一方でサンプル数が少ない場合、極端な値を取る可能性があります。例えばサイコロを2回投げる場合、1が連続して2回出るケースは珍しくありません。期待値は3.5にも関わらず、実際には1を連続して得られるのです。
正確な確率を得たい場合、非常に多くのサンプル数を必要とするのは、試行回数が少ないと正しいデータを得られないことがよくあるからです。
例えば医薬品の研究開発では、臨床試験をするときに何万人もの治験データを集めます。この理由として、多くのデータを集めれば大数の法則によって正しい治験結果を得られやすくなるからです。
また銀行や保険会社が倒産しないのは、大数の法則を利用しているからです。銀行は何万社にお金を貸しており、お金を貸す企業数が多ければ、会社が倒産する確率は一定割合に落ち着きます。生命保険会社についても、何百万人もの加入者がいれば、死亡する割合は特定の値に収束します。
データ数が多ければ多いほど、理論的な確率へと収束するため、より正確に起こる確率を計算できるようになるのです。
平均値(または合計)が正規分布となる中心極限定理
大数の法則を学べば、中心極限定理を理解することができます。大数の法則と中心極限定理というのは、ほぼ同じ意味です。
大数の法則では、確率が理論値に収束します。一方で中心極限定理では、事象の平均(または合計)が正規分布となります。どのようなデータであっても、試行回数が多くなると正規分布になるのが中心極限定理というわけです。
大数の法則をより詳細にしたのが中心極限定理であると理解しましょう。
中心極限定理の場合、正規分布へ近似できるため、あらゆるパターンについて確率を計算できるようになります。そのため期待値へ収束する大数の法則よりも、利用する場面が多いのです。
中心極限定理とは何か?正規分布でないケースは多い
それでは、中心極限定理とは何かより詳しく確認していきましょう。中心極限定理でよくある勘違いとしては、「すべての分布について正規分布になる」と理解することです。
ただ当然ながら、すべての分布が正規分布になることはありません。正規分布ではないデータは非常にたくさんあります。例えば、賛成(0)または反対(1)を問う投票での結果は以下のようになります。
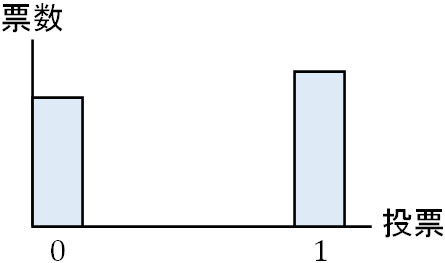
このように、正規分布ではありません。
他には、目の数が「2,2,4,4,5,6」という特殊なサイコロを一回投げる場合、以下のような分布になります。
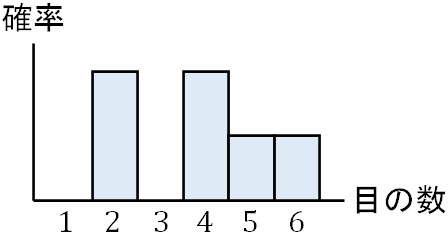
それでは、どのようなときに中心極限定理が有効なのでしょうか。中心極限定理では、「試行回数が多い場合、平均または合計が正規分布になる」といえます。つまりデータを集めるだけでは不十分であり、平均または合計をしなければ正規分布に近似できないと理解しましょう。
データをたくさん集めると正規分布になる:平均値・合計の事例
そこでデータをたくさん集めるとき、平均値または合計を計算しましょう。例として、目の数が「2,2,4,4,5,6」である特殊なサイコロを2回投げ、その合計について確率を数えましょう。
試行回数が少ない場合、正規分布にはなりません。特殊なサイコロを2回投げる場合、確率は以下のようになります。
- 合計が4:\(\left(\displaystyle\frac{1}{3}\right)^2=\displaystyle\frac{1}{9}\)
- 合計が6:\(2×\left(\displaystyle\frac{1}{3}\right)^2=\displaystyle\frac{2}{9}\)
- 合計が7:\(2×\left(\displaystyle\frac{1}{3}\right)\left(\displaystyle\frac{1}{6}\right)=\displaystyle\frac{1}{9}\)
- 合計が8:\(\left(\displaystyle\frac{1}{3}\right)^2\)\(+2×\left(\displaystyle\frac{1}{3}\right)\left(\displaystyle\frac{1}{6}\right)\)\(=\displaystyle\frac{2}{9}\)
- 合計が9:\(2×\left(\displaystyle\frac{1}{3}\right)\left(\displaystyle\frac{1}{6}\right)=\displaystyle\frac{1}{9}\)
- 合計が10:\(2×\left(\displaystyle\frac{1}{3}\right)\left(\displaystyle\frac{1}{6}\right)\)\(+\left(\displaystyle\frac{1}{6}\right)^2\)\(=\displaystyle\frac{5}{36}\)
- 合計が11:\(2×\left(\displaystyle\frac{1}{6}\right)^2=\displaystyle\frac{1}{18}\)
- 合計が12:\(\left(\displaystyle\frac{1}{6}\right)^2=\displaystyle\frac{1}{36}\)

それでは特殊なサイコロについて、2回ではなく、100回投げるときの合計はどのようになるでしょうか。この場合、以下のようなヒストグラムになります。
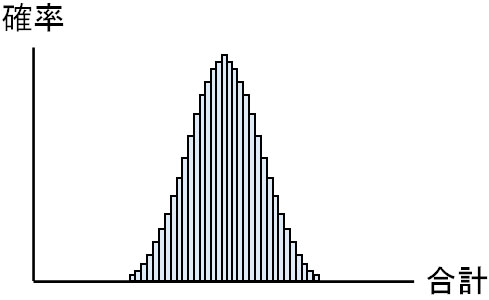
特殊なサイコロであっても、イカサマのゲームであったとしても、試行回数が多ければ平均または合計を正規分布へ近似できます。正規分布とみなすことができるため、期待値や分散、標準偏差の計算ができるというわけです。
そこで、以下のように考えましょう。
- 同じ事象について何度も同じ操作を行うとき、試行回数が多くなると、平均または合計は正規分布とみなせる
これが中心極限定理です。正規分布とみなすことができれば、特定の事象が起こる確率を計算できます。中心極限定理を利用すれば、正規分布を利用することでさまざまな値を得ることができるのです。
全データがなくても、中心極限定理を利用することによって特定の事象が起こる確率を予測することができるため、中心極限定理は非常に多くの場面で利用されています。
統計学で中心極限定理は重要
サンプル数が多い場合、二項分布やイカサマのサイコロを含め、ほとんどの場面で成り立つのが中心極限定理です。ほとんどの場面というのは、コーシー分布(平均や分散が存在しない分布)では成り立たないからです。ただそれ以外では、すべての場面で中心極限定理が適用されます。
要は、平均や分散が存在しない特殊な場合を除き、中心極限定理を利用することによって正規分布とみなすことができるのです。
統計データを処理するとき、正規分布とみなすことができるのは非常に便利です。正規分布へ近似すれば期待値や分散、標準偏差を計算することによって、特定の事象(確率変数)が起こる確率を計算できます。
ただ、中心極限定理は「すべての分布が正規分布になる」という意味ではありません。サンプル数が多い場合、平均や合計が正規分布になるのが中心極限定理です。中心極限定理について、この性質を理解しましょう。






