物理で学ぶ内容に円運動があります。同じ速さで円軌道を描く運動をする場合、円運動と呼ばれています。
円運動を理解するためには、角速度を学ばなければいけません。新たな概念を学ぶことになるため、円運動は理解が難しいです。また計算問題を解くためには、公式を覚えなければいけません。それに加えて、公式の意味を理解しましょう。
力学では、円運動の中でも等速円運動を学びます。このとき中心に向かって発生する力が向心力です。また、円運動にとっての慣性力を遠心力といいます。向心力と遠心力は同じ大きさの力であり、力の大きさを計算できるようにならなければいけません。
それでは、角速度とは何なのでしょうか。また、どのようにして向心力を計算すればいいのでしょうか。円運動で利用される公式や向心力・遠心力の計算方法を解説していきます。
もくじ
等速円運動では、ベクトルを考慮した速さが変化する
等速直線運動では、常に速度が同じです。等速円運動でも、同じ速さで円運動をします。以下のように、常に速さ\(v\)で円運動をするのが等速円運動です。
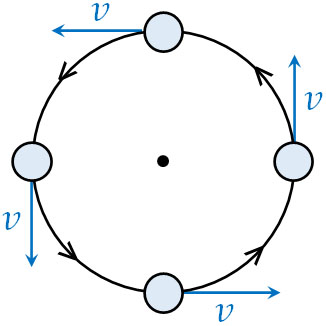
ただ円運動の場合、ベクトルを考慮すると速度は変化します。例えば上向きの速度を正とする場合、運動の向きを考慮する場合の速度は以下のようになります。
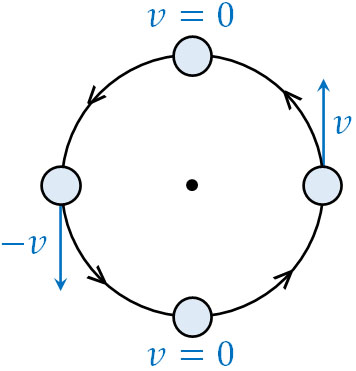
つまりスピードは同じであるものの、ベクトルを考慮する場合は速度が異なるのです。これが等速直線運動と等速円運動の違いです。物理ではベクトルを考慮して速度の計算をする必要があるため、力の向きを確認しましょう。
・速度は円軌道の接線方向となる
なお円運動での速度というのは、円軌道の接線方向となります。これについては、先ほどの図を確認すれば理解できます。速度を計算するとき、必ず円軌道に対して接線を引きましょう。
円運動では中心へ向かう力(向心力)を生じる
前述の通り、円運動ではベクトルを考慮した速度が変化します。速度が変化するとき、必ず加速度が存在します。それでは、円運動で加速度はどこに生じているのでしょうか。
イメージとしては、ハンマー投げの場面がわかりやすいです。ハンマー投げではワイヤーに鉄球をつけ、高速で回転させます。このとき、ハンマー投げ選手はワイヤーを常に引っ張る必要があります。言い換えると、ワイヤーには張力がかかっています。
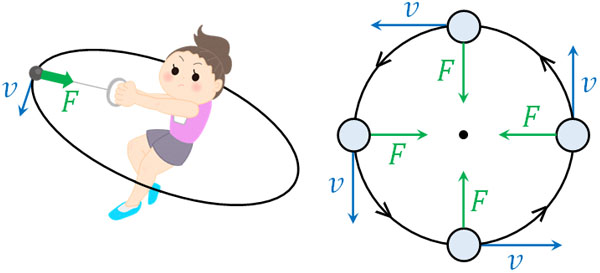
つまり回転している物体では、円の中心に対して一定の力\(F\)が加わっています。この力を向心力といいます。
\(F=ma\)であり、向心力が中心に向かって働いているというのは、言い換えると、中心に向かって一定の加速度\(a\)が加わっていることになります。
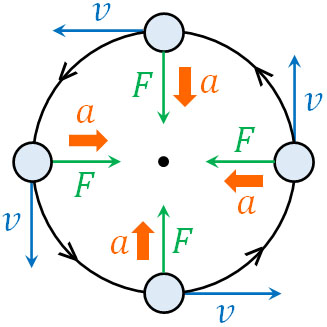
向心力によって加速度が発生しているため、ベクトルを考慮して速さを確認する場合、速度が変化するのです。円運動を学ぶとき、加速度の向きと向心力の概念を理解しましょう。
弧度法を利用し、角速度\(ω\)を用いる
円運動を学ぶとき、もう一つ理解しなければいけない概念に角速度があります。角速度は\(ω\)(オメガ)で表され、これは「一秒間で角度\(ω\)を移動する」ことを意味します。
なお角速度の計算で利用するのは弧度法です。つまりθは180°や90°ではなく、πや\(\displaystyle\frac{π}{2}\)で表されます。弧度法では、360°のときは2πです。また180°のときはπです。90°のときは\(\displaystyle\frac{π}{2}\)です。
このとき半径をrとすると、2π(360°)の円周は2πrです。直径(2r)に円周率(π)をかけると、当然ながら円周の長さ\(l\)を得ることができます。またπ(180°)の弧の長さはπrです。θは弧度法での角度であるため、弧の長さ\(l\)は\(l=rθ\)によって計算できます。
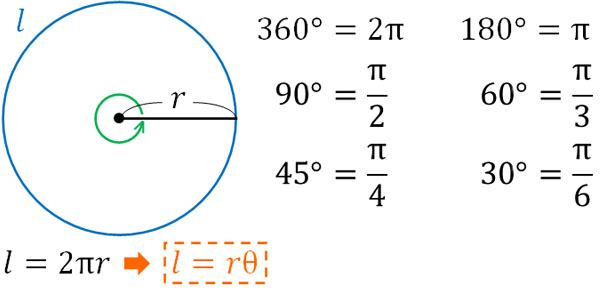
θが2π(360°)の場合、\(θ=2π\)を代入すると、\(l=2πr\)になります。またθがπ(180°)の場合、\(θ=π\)を代入すると、弧の長さは円周の半分である\(l=πr\)と計算できます。そのため、この式に間違いはないとわかります。なお、この式は等速円運動の公式を得るときに重要です。
弧度法での角度の表し方を理解した後、角速度\(ω\)を学びましょう。前述の通り、角速度は1秒間に進む角度のスピードを表します。例えば角速度が\(\displaystyle\frac{π}{6}\)の場合、1秒間に\(\displaystyle\frac{π}{6}\)進みます。
言い換えると、1秒間で30°ずつ回転します。また6秒経過すればπ(180°)進むので反転し、12秒経過すれば元の位置に戻ります。
等速円運動の速度と加速度を得る公式の証明
それでは、等速円運動の速度\(v\)と加速度\(a\)の公式を導き出しましょう。1回転するために必要な時間\(T\)を周期といいます。例えば角速度が\(\displaystyle\frac{π}{6}\)の場合、前述の通り1秒間に\(\displaystyle\frac{π}{6}\)進むため、周期\(T\)は12秒です。
そのため、角速度\(ω\)と周期\(T\)をかけると2πになります。
- \(ωT=2π\) – ①
また速さ\(v\)で\(T\)秒が経過すると、円を一周することになります。言い換えると、速さ\(v\)と\(T\)秒をかけると、弧の長さ\(l\)を得ることができます。
- \(vT=2πr\) – ②
そこで、①を②に代入しましょう。
\(vT=2πr\)
\(vT=ωTr\)
\(v=rω\)
こうして、角速度\(ω\)と円の半径\(r\)を用いて速度\(v\)を得る公式を導くことができました。
・等速円運動の加速度の公式
次に等速円運動の加速度を得る公式を導き出しましょう。ベクトルを考慮する場合、前述の通り速度が変化します。また、円運動では速さの向きも変わります。速度が変化するというのは、加速度が関わっていることを意味します。そこで、速度の変化を計算することで加速度を求めましょう。
角速度\(ω\)で\(t\)秒が経過すると、回転する角度は\(ωt\)です。このとき、回転する前の速さを\(v_A\)、\(t\)経過後の速さを\(v_B\)とします。等速円運動であるため、\(v_A=v_B\)です。ただ加速度が加わることにより、向きが変化しています。
そこで\(v_A\)と\(v_B\)について、向きを考慮した速度の変化\(Δv\)を計算しましょう。図にすると、\(Δv\)は以下のようになります。
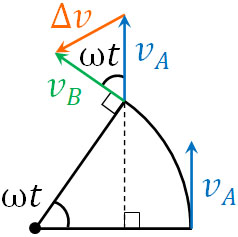
次に、\(t\)をできるだけ短くしましょう。経過時間\(t\)が短い場合、角度\(wt\)は非常に小さくなります。また\(v_A\)と\(v_B\)によって作られる角度は\(wt\)であり、角度は小さくなります。
このとき、\(v_A\)と\(v_B\)によって作られる三角形は「中心角が\(wt\)、半径\(v\)のおうぎ形」とみなすことができます。
またおうぎ形の弧の長さ\(l\)は前述の通り、\(l=rθ\)によって計算できます。半径は\(r\)ではなく\(v\)であり、θ(角度)は\(ωt\)です。そのため、\(l=vωt\)となります。
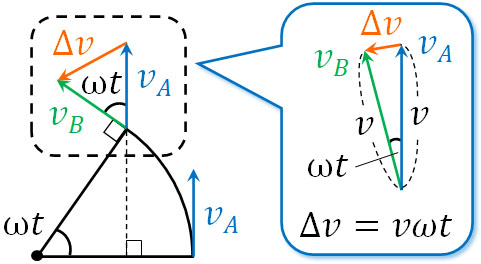
重要なのは、弧の長さ\(l\)を速度の変化\(Δv\)とみなせることです。速度の変化\(Δv\)は直線であり、曲線ではありません。そのため厳密には、弧の長さ\(l\)と速度の変化\(Δv\)は違います。
ただ経過時間\(t\)は非常に短いため、\(Δv\)は弧の長さとほぼ等しくなります。そこで\(l\)を\(Δv\)に変えることで、以下の式を得ましょう。
\(Δv=vωt\)
また、両辺を\(t\)で割ると以下のようになります。
\(\displaystyle\frac{Δv}{t}=vω\)
速度\(Δv\)を経過時間\(t\)で割ると、加速度\(a\)を得られることは既に理解していると思います。加速度というのは、時間経過によってどれだけの割合で速度が上昇するのかを表します。そのため、速度を時間で割ると加速度になるのです。
そこで、\(\displaystyle\frac{Δv}{t}\)を加速度\(a\)に変えましょう。
- \(a=vω\)
こうして、等速円運動で加速度を得る公式を導き出すことができました。
なお時間\(t\)が非常に短い場合、速度の変化\(Δv\)は\(v_B\)に対してほぼ直角になります。図にすると以下のようになります。
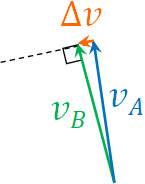
前述の通り、等速円運動の速度は円の接線方向に向きます。つまり速度の変化\(Δv\)は円の中心に向かって発生しているとわかります。また速度の変化\(Δv\)が円の中心にベクトルが向いているため、加速度\(a\)の向きも円の中心です。
向心力では、円の中心に向かって力が発生していると解説しました。これは、経過時間\(t\)が短い場合、円の中心に向かって速度の変化が起こっているからなのです。
・加速度の公式を変形する
なお前述の通り、\(v=rω\)です。そこで、\(v=rω\)を\(a=vω\)に代入すると以下のようになります。
- \(a=rω^2\)
また\(v=rω\)より、\(ω=\displaystyle\frac{v}{r}\)です。そこで、\(ω=\displaystyle\frac{v}{r}\)を\(a=vω\)に代入しましょう。
- \(a=\displaystyle\frac{v^2}{r}\)
つまり、等速円運動で加速度\(a\)を求める方法は3つあります。
- \(a=vω=rω^2=\displaystyle\frac{v^2}{r}\)
\(v=rω\)を利用することで、このように公式の変形が可能です。
等速円運動の公式の覚え方と変形
実際に等速円運動の計算をするとき、ここまで解説した公式の証明を利用して問題を解くことはありません。そのため、等速円運動の計算問題を解くときは公式を覚えましょう。
覚え方としては、半径\(r\)に角速度\(ω\)をかけると速度\(v\)の公式になります。また速度\(v\)に角速度\(ω\)をかけると加速度\(a\)の公式になります。

先ほど説明した通り、\(v=rω\)を利用することで加速度の公式を変形できます。加速度の公式3つをすべて覚える必要はなく、一つだけ覚えれば十分です。
公式を利用し、角速度や向心力を計算する
それでは、等速円運動の公式を利用して角速度や速さ、加速度、向心力を計算しましょう。以下の問題の答えは何でしょうか。
- 糸につながれた質量\(m\)の球がなめらかな床を速さ\(v\)、半径\(r\)で等速円運動をしています。
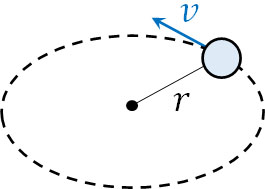
- 球が一回転するために必要な時間(周期)\(T\)を求めましょう。
- 球に働く力を求めましょう。
1) 球が一回転するために必要な時間(周期)\(T\)を求めましょう
まず、周期\(T\)を利用する式を作りましょう。球は1秒で\(ω\)進み、\(T\)秒で一周します。また2πは360°であるため、以下の式を作ることができます。
\(ωT=2π\)
等速円運動の公式より、\(v=rω\)です。つまり、\(ω=\displaystyle\frac{v}{r}\)です。そこで、\(ω=\displaystyle\frac{v}{r}\)を先ほどの式に代入しましょう。
\(ωT=2π\)
\(\displaystyle\frac{v}{r}×T=2π\)
\(T=\displaystyle\frac{2πr}{v}\)
こうして、\(T=\displaystyle\frac{2πr}{v}\)と計算できました。
2) 球に働く力を求めましょう
球に働く力というのは、要は向心力を計算すればいいとわかります。力を計算するためには加速度が必要です。等速円運動の公式より、\(a=\displaystyle\frac{v^2}{r}\)です。
また球の質量は\(m\)です。力の計算をするとき、\(F=ma\)であるため、\(a=\displaystyle\frac{v^2}{r}\)を代入しましょう。
\(F=ma\)
\(F=\displaystyle\frac{mv^2}{r}\)
こうして、球に働く向心力を計算できました。\(F=\displaystyle\frac{mv^2}{r}\)の力が円の中心に向かって働きます。
遠心力:慣性力の円バージョンが遠心力
向心力を学んだら、同時に遠心力を理解しましょう。遠心力は多くの人が利用している言葉であり、向心力と遠心力はほぼ同じ概念です。
遊園地など、等速円運動で回転しているイスにあなたが座ると、イスは外側に引っ張られます。これが遠心力です。

回転している物体は円の中心に力が加わります。一方であなたが回転している物体に乗っている場合、円の中心とは反対側に力が加わるのです。
この理由は慣性力です。直線に加速している乗り物にあなたが乗っている場合、乗り物の進行方向とは逆向きに加速度が加わります。同様に、回転している乗り物にあなたが乗っている場合、向心力とは逆向きに加速度が加わるのです。遠心力とは、向心力によって生じる慣性力なのです。
そのためベクトル(力の向き)は反対であるものの、向心力と遠心力の大きさは同じです。また、あなたは乗り物に乗っていて動いていないため、水平方向の力がつり合っています。
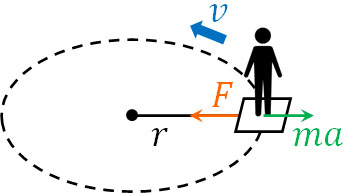
そこで、遠心力を計算しましょう。向心力の加速度と遠心力の加速度\(a\)は同じです(向きは反対)。そこで向心力を\(F\)、あなたの体重を\(m\)とすると、力のつり合いの式は以下のようになります。
\(F=ma\)
等速円運動の公式より、\(a=\displaystyle\frac{v^2}{r}\)です。そのため半径\(r\)の円を速さ\(v\)で回転している場合、あなたに加わる遠心力は\(\displaystyle\frac{mv^2}{r}\)です。
角度がある場合の計算方法:円すい振り子の問題
それでは、遠心力を含む物理の問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 長さ\(l\)の糸を天井と質量\(m\)の重りに固定し、下図のように角度θを保って等速円運動をしています。糸に働く張力、円運動の速さ、円の周期を求めましょう。なお、重力加速度は\(g\)です。
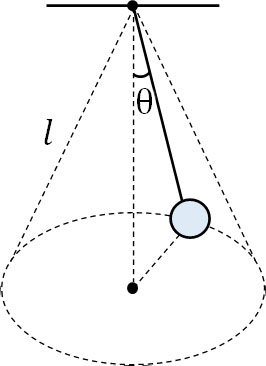
・糸の張力\(S\)
まず、糸の張力\(S\)を計算しましょう。鉛直方向だけに着目すると、球の高さは一定です。つまり、鉛直方向では力がつり合っています。
そこで、張力\(S\)と重りによる力が等しくなるように式を作りましょう。そうすると、以下の式を作れます。
\(Scosθ=mg\)
\(S=\displaystyle\frac{mg}{cosθ}\)
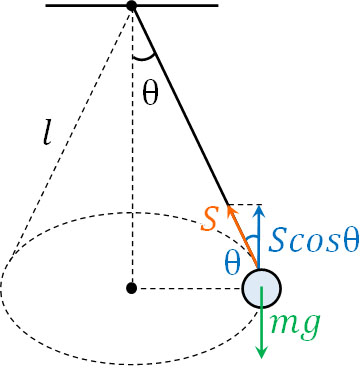
こうして、糸の張力は\(S=\displaystyle\frac{mg}{cosθ}\)とわかります。
・円運動の速さ\(v\)
あなたが球の上に乗っていると仮定すると、あなたは球から動いていないため、水平方向では力がつり合っています。言い換えると、向心力と遠心力がつり合っています。この場合、以下の力のつり合いの式を作ることができます。
\(Ssinθ=ma\)
\(S=\displaystyle\frac{mg}{cosθ}\)を代入。
\(\displaystyle\frac{mg}{cosθ}×sinθ=ma\)
\(a=gtanθ\)
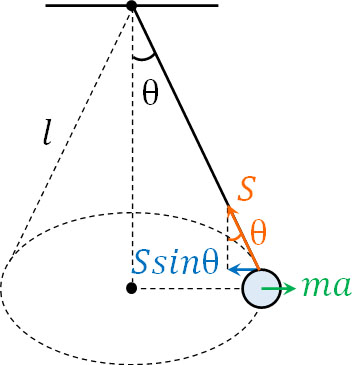
なお等速円運動の公式より、\(a=\displaystyle\frac{v^2}{r}\)です。また今回の問題では、円の半径\(r\)は\(lsinθ\)です。つまり、\(a=\displaystyle\frac{v^2}{lsinθ}\)となります。そこで、\(a=\displaystyle\frac{v^2}{lsinθ}\)を\(a=gtanθ\)に代入しましょう。
\(a=gtanθ\)
\(\displaystyle\frac{v^2}{lsinθ}=gtanθ\)
\(v^2=gltanθ·sinθ\)
\(v=\sqrt{gltanθ·sinθ}\) (\(v>0\))
こうして、速さ\(v\)は\(\sqrt{gltanθ·sinθ}\)とわかりました。
・円の周期\(T\)
角速度が\(ω\)の場合、1秒で\(ω\)進みます。また\(T\)秒で円を一周するため、以下の式を作れます。
\(ωT=2π\)
\(T=\displaystyle\frac{2π}{ω}\) – ①
等速円運動の公式より、\(v=rω\)です。つまり、\(v=\sqrt{gltanθ·sinθ}\)と\(r=lsinθ\)より、以下のようになります。
\(v=rω\)
\(\sqrt{gltanθ·sinθ}=lsinθ·ω\)
\(ω=\sqrt{\displaystyle\frac{gtanθ}{lsinθ}}\) – ②
そこで、②を①に代入しましょう。
\(T=\displaystyle\frac{2π}{ω}\)
\(T=\displaystyle\frac{2π\sqrt{lsinθ}}{\sqrt{gtanθ}}\)
\(T=\displaystyle\frac{2π\sqrt{lcosθ}}{\sqrt{g}}\)
こうして、周期\(T\)は\(\displaystyle\frac{2π\sqrt{lcosθ}}{\sqrt{g}}\)と計算できました。
等速円運動でない場合の計算:運動方程式と力学的エネルギー保存則の利用
ここまで、等速円運動について解説してきました。ただ場合によっては、等速円運動ではない計算問題を解かなければいけないことがあります。例えばジェットコースターのように、上下を一周する円運動を考えてみましょう。

ジェットコースターのスピードが十分ではない場合、ジェットコースターは円を回ることができません。円を回転するとき、重力がかかります。重力による影響の分だけ、円を上昇するにしたがって速さは落ちていきます。一方で円を下降するとき、重力によって速さは上昇します。
このように考えると、円を回転させるときに物体の高さが変化するため、等速円運動ではないとわかります。
なお等速円運動ではない場合であっても、基本的な考え方は同じです。ただ等速円運動ではない場合、重力によって円運動するときの速さが変わります。そこで、運動方程式と力学的エネルギー保存則を利用することで式を作りましょう。
重要なのは、向心力が行う仕事はゼロである点です。前述の通り、速さ\(v\)は円の接線方向になります。向心力\(F\)に対して、物体は常に垂直に動いているため、向心力\(F\)による仕事は0です。そのため力学的エネルギー保存則を円運動で利用する場合、向心力による仕事を無視できます。
その代わり、円運動をするときに物体の位置が高くなるため、位置エネルギーが高くなります。それに伴い、物体のスピードが遅くなります。そこで、変化前と変化後でのエネルギーの変化を利用して式を作りましょう。
物体が1回転するための条件
それでは、実際に計算問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 長さ\(l\)の糸に質量\(m\)の物体をつけ、最下点から初速\(v_0\)を加えると円運動をしました。なお、下図のように鉛直方向と糸との角度をθ、重量加速度を\(g\)とします。
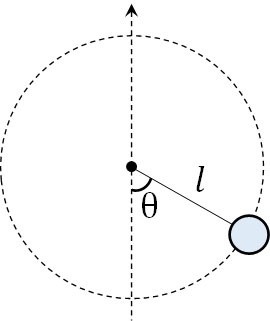
- 角度θのとき、物体の速さ\(v\)を求めましょう。
- 角度θのとき、張力\(S\)を求めましょう。
- 物体が一回転するために必要な\(v_0\)の条件を求めましょう。
1) 角度θのとき、物体の速さ\(v\)を求めましょう
運動方程式であっても、力学的エネルギー保存則であっても、物体の速さ\(v\)に関する式を作ることができます。ただ張力が与えられていないため、張力を利用せずに物体の速さを求めましょう。そこで、力学的エネルギー保存則を利用します。
初速\(v_0\)が加えられているため、物体がもつエネルギーは\(\displaystyle\frac{1}{2}mv_0^2\)です。その後、角度θのとき、物体は位置エネルギーと運動エネルギーをもちます。
物体の高さは以下のように計算できます。
\(l-lcosθ\)
\(l(1-cosθ)\)
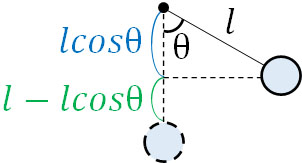
つまり、角度θのときに物体がもつ位置エネルギーは\(mgl(1-cosθ)\)です。また、角度θのときに物体がもつ運動エネルギーは\(\displaystyle\frac{1}{2}mv^2\)です。そのため力学的エネルギー保存則を利用し、以下の式を作れます。
\(\displaystyle\frac{1}{2}mv_0^2=mgl(1-cosθ)+\displaystyle\frac{1}{2}mv^2\)
\(v_0^2=2gl(1-cosθ)+v^2\)
\(v^2=v_0^2-2gl(1-cosθ)\)
\(v=\sqrt{v_0^2-2gl(1-cosθ)}\) (\(v>0\))
こうして、角度θのときの速さは\(\sqrt{v_0^2-2gl(1-cosθ)}\) とわかりました。
2) 角度θのとき、張力\(S\)を求めましょう
張力(向心力)\(S\)と遠心力\(mgcosθ\)による力のつり合いを考え、\(S=mgcosθ\)の式を作ってはいけません。鉛直方向では、物体は静止していません。また、重力による力を受けることによって速度が変化しており、力はつり合っていません。
そこで力のつり合いの式を作る代わりとして、運動方程式を作りましょう。
円運動をするためには、向心力が働く必要があります。向心力があるからこそ、遠心力が働くことによって物体は円運動をするのです。そこで、向心力を基準にして運動方程式を作りましょう。向心力は以下の方法によって計算できます。
- 向心力(遠心力) = 糸の張力 - 重力による影響
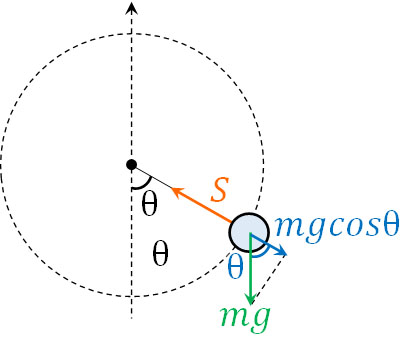
そこで、以下の式を作りましょう。
- 向心力\(=S-mgcosθ\)
なお運動方程式より、\(F=ma\)です。そのため、\(S-mgcosθ=ma\)となります。
重要なのは、円運動をするときは\(a=\displaystyle\frac{v^2}{r}\)を利用できることです。これまで説明した通り、円運動の公式では「非常に短い時間に働く力(向心力)」を利用しています。
等速円運動ではないため、角速度ωと速さ\(v\)は変化します。ただ糸の長さ\(l\)(円の半径\(r\))は同じです。また角度θのとき(速さ\(v\)のとき)に生じる瞬間的な加速度がわかればいいため、\(a=\displaystyle\frac{v^2}{r}\)を利用できるのです。
そこで、\(a=\displaystyle\frac{v^2}{r}\)を\(S-mgcosθ=ma\)に代入しましょう。
\(S-mgcosθ=ma\)
\(S-mgcosθ=m\displaystyle\frac{v^2}{l}\)
\(S=m\displaystyle\frac{v^2}{l}+mgcosθ\)
また問題1の答えより、\(v^2=v_0^2-2gl(1-cosθ)\)です。そこで、\(v^2=v_0^2-2gl(1-cosθ)\)を代入しましょう。
\(S=m\displaystyle\frac{v^2}{l}+mgcosθ\)
\(S=m\displaystyle\frac{v_0^2-2gl(1-cosθ)}{l}+mgcosθ\)
\(S=m\displaystyle\frac{v_0^2}{l}-2mg(1-cosθ)+mgcosθ\)
\(S=m\displaystyle\frac{v_0^2}{l}+mg(3cosθ-2)\)
こうして、\(S=m\displaystyle\frac{v_0^2}{l}+mg(3cosθ-2)\)が答えになります。
3) 物体が一回転するために必要な\(v_0\)の条件を求めましょう
物体が回転しないとき、向心力が0になります。言い換えると、中心に向かう加速度が0になるときに物体は回転をやめます。速さ\(v\)が0になるときに物体が回転をやめるわけではありません。速さがあっても、物体が一回転せずに円運動をやめる例は多いです。
そのため物体が一回転する条件(糸がたるまない条件)として、円の中心に向かって常に加速度が働いていることがあげられます。
それでは、重力による影響が最も大きくなる点はどこでしょうか。最も高い位置で重力による影響が最も強くなり、θがπ(=180°)のときに円運動による加速度が最も小さくなると想像できます。
また先ほど解説した通り、\(S-mgcosθ=ma\)です。そのため、向心力(張力)は以下のように表すことができます。
\(S-mgcosθ=ma\)
\(S=ma+mgcosθ\)
\(cosθ=-1\)のとき、向心力が最も小さくなります。つまり式からも、\(θ=π\)のときに加速度が最も小さくなるとわかります。
また問題2より、張力\(S\)は以下の式になると既に計算しています。
\(S=m\displaystyle\frac{v_0^2}{l}+mg(3cosθ-2)\)
そこで、張力(向心力)がゼロ以上となる式を作って計算しましょう。なお\(θ=π\)であるため、式は以下のようになります。
\(m\displaystyle\frac{v_0^2}{l}+mg(3cosπ-2)≧0\)
\(m\displaystyle\frac{v_0^2}{l}-5mg≧0\)
\(m\displaystyle\frac{v_0^2}{l}≧5mg\)
\(v_0^2≧5gl\)
\(v_0≧\sqrt{5gl}\) \((v_0>0)\)
こうして、物体が円運動をするためには、初速度\(v_0\)は最低でも\(\sqrt{5gl}\)よりも速くなければいけないと計算できました。
円運動の公式を利用して計算する
物理で円運動を学ぶとき、内容は難しいです。角度は弧度法を利用しますし、角速度という新たな概念を理解しなければいけません。また覚えなくてもいい物理の公式は多いものの、円運動の計算では公式を覚える必要があります。
なお物体が運動する向きではなく、円運動では円の中心に向かって常に力が加わります。言い換えると、円の中心に向かって加速度が加わります。
等速直線運動や等加速度直線運動とは異なる概念が円運動です。力のつり合いや運動方程式、力学的エネルギー保存則を利用して式を作るものの、円運動に特有の考え方を理解しましょう。
円運動の性質を学べば、等速円運動ではないケースであっても式を作れます。そこで公式の意味や式の作り方を理解し、式を作れるようになりましょう。