統計学で確率論を学ぶとき、教科書にチェビシェフの不等式が出てくることがあります。ただ多くの人にとって、チェビシェフの不等式は難しいです。
数式を見てもチェビシェフの不等式を理解できるようになることはありません。そこで数式の意味を学びましょう。要は、チェビシェフの不等式が何を表しているのか理解するのです。
すべての確率変数Xに対して成立するのがチェビシェフの不等式です。またチェビシェフの不等式を利用すれば、グラフの形や分布がわからなかったとしても、範囲外の確率がいくら含まれているのか把握できるようになります。
式を見ても理解できないものの、概念を学び、そのあとに例題での確認や証明をすれば内容を把握できます。そこでマルコフの不等式と共に、チェビシェフの不等式を解説していきます。
もくじ
統計学でのチェビシェフの不等式と公式の意味
チェビシェフの不等式には2つの種類があり、この記事で解説するのは確率論でのチェビシェフの不等式になります。
統計学で学ぶチェビシェフの不等式は以下の公式によって表されます。
- \(P(|X-μ|≥kσ)\)\(≤\displaystyle\frac{1}{k^2}\)
すべての分布について、この公式が成立します。正規分布だけでなく、特殊な形をした分布であっても成り立つため、統計学では有用な公式です。なおこの公式をみても、まったく意味を理解できないと思います。それでは、この公式は何を意味しているのでしょうか。
\(k\)は任意の数であり、どのような値を入れても問題ありません。また\(μ\)は平均(期待値)であり、\(σ\)は標準偏差です。
まず、左側\(P(|X-μ|≥kσ)\)から確認していきましょう。\(|X-μ|\)というのは、確率変数Xから平均値\(μ\)を引くことを意味します。正規分布を標準正規分布に直すとき、\(X-μ\)によって、グラフの中心\(μ\)を0に移動したと思います。同じように、確率変数Xから平均値\(μ\)を引きましょう。
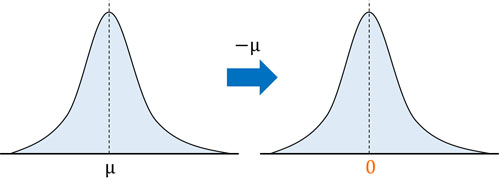
その後、標準正規分布を作るとき、すべての正規分布の横幅を同じにするために\(σ\)で割りました。
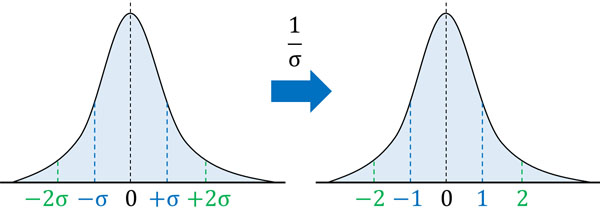
こうして、正規分布から標準正規分布へ変換するための公式を得られます。
- \(Z=\displaystyle\frac{X-μ}{σ}\)
なお正規分布では、すべてのグラフについて「中心からの長さ」と「範囲に含まれる確率」が決まっています。
- 平均値から「標準偏差×1」の範囲:データ全体の68.3%
- 平均値から「標準偏差×2」の範囲:データ全体の95.5%
- 平均値から「標準偏差×3」の範囲:データ全体の99.7%
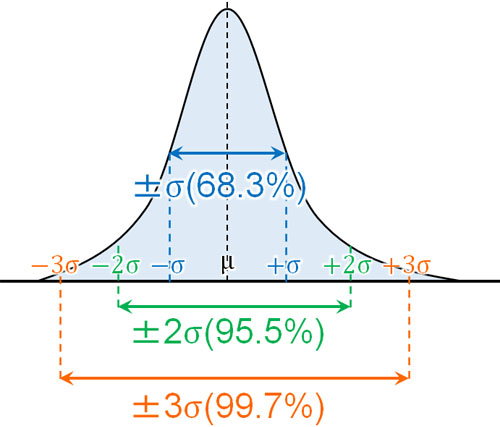
ここまでの内容を復習すれば、チェビシェフの不等式の意味を理解できます。標準正規分布では確率変数Zを利用します。確率変数Zが2よりも大きい場合、トップ(または下位)4.5%に含まれることになります。
そこで、確率変数Zを任意の数\(k\)に変えましょう。また確率変数Xから平均\(μ\)を引くとき、絶対値をつけましょう。そうすると、以下の式に変えることができます。
\(k=\displaystyle\frac{|X-μ|}{σ}\)
\(|X-μ|=kσ\)
こうして、\(P(|X-μ|≥kσ)\)とほぼ同じ形にすることができました。つまり\(|X-μ|≥kσ\)というのは、確率変数Xが含まれる場所を指します。
例えば\(k=2\)の場合、\(|X-μ|≥2σ\)です。前述の通り、中心から\(2σ\)の範囲にはデータ全体の95.5%が含まれています。ただ\(|X-μ|≥2σ\)となっているため、確率変数Xはデータ全体の95.5%よりも大きい値(または小さい値)になります。
このように\(P(|X-μ|≥kσ)\)というのは、\(|X-μ|\)が\(kσ\)よりも大きい値(または小さい値)のときの確率を指します。
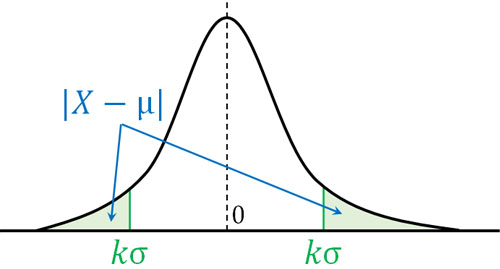
標準正規分布を利用してチェビシェフの不等式の左辺を解説しましたが、前述の通り正規分布だけでなく、すべての分布でチェビシェフの不等式が成り立ちます。
チェビシェフの不等式の右辺は何を意味しているのか
次に、チェビシェフの不等式の右辺を確認しましょう。チェビシェフの不等式の右辺は\(\displaystyle\frac{1}{k^2}\)です。
\(k\)というのは、任意の数であることを先に述べました。正規分布で\(|X-μ|\)が含まれる範囲を31.7%(データ全体の68.3%以外)にしたい場合、\(k=1\)にします。一方、正規分布で\(|X-μ|\)が含まれる範囲を4.5%(データ全体の95.5%以外)にしたい場合、\(k=2\)にします。
例えば\(k=2\)とする場合、チェビシェフの不等式は以下のようになります。
- \(P(|X-μ|≥2σ)\)\(≤\displaystyle\frac{1}{2^2}\)
\(\displaystyle\frac{1}{2^2}=0.25\)です。つまり\(k=2\)の場合、\(|X-μ|\)が\(2σ\)よりも大きい値(または小さい値)になる確率は0.25%(25%)以下であることを示しています。
正規分布の場合、前述の通り\(k=2\)の場合だと\(|X-μ|≥2σ\)となるケースは4.5%(データ全体の95.5%以外)になります。ただチェビシェフの不等式は正規分布だけでなく、すべてのグラフに当てはまる公式であるため、正規分布よりも\(|X-μ|\)が含まれる範囲は広くなります。
例題を利用し、チェビシェフの不等式を理解する
それでは、例題を利用してチェビシェフの不等式を理解しましょう。確率変数Xの分布に関係なく成立するため、どのようなデータであってもチェビシェフの不等式を使うことができます。
例えば、以下の問題の答えは何でしょうか。
- テストの平均点は60点であり、標準偏差は15です。平均点よりも30点以上、離れている人の割合の最大値はいくらと予想できるでしょうか。
\(kσ\)というのは、中心(平均)からどれだけ離れているのかを表します。標準偏差\(σ\)は15であり、平均点よりも30点の高得点(または低い点数)を取っている人というのは、\(30=15k\)より、\(k=2\)を想定しましょう。
また\(P(|X-60|≥2σ)\)というのは、\(|X-60|\)が\(2σ(30)\)よりも大きい値(または小さい値)を指します。そのため、平均点よりも30点以上離れている確率を意味します。
なお\(k=2\)であるため、\(\displaystyle\frac{1}{2^2}=0.25\)です。そのため、以下のようになります。
\(P(|X-60|≥2σ)≤0.25\)
そのためすべてのデータについて、平均点よりも30点以上離れている人の割合は最大25%であるとわかります。
マルコフの不等式の公式と意味
数式を見ても、チェビシェフの不等式を理解することはできません。ただ、式の中身を一つずつ確認していけば、何を意味しているのか分かるようになります。
次のステップとして、チェビシェフの不等式が成り立つことを証明しましょう。チェビシェフの不等式を証明する前に、必ず理解しなければいけないのがマルコフの不等式です。\(a>0\)のとき、以下がマルコフの不等式です。
- \(P(X≥a)\)\(≤\displaystyle\frac{E(X)}{a}\)
チェビシェフの不等式と比べて、式が似ています。それでは、マルコフの不等式は何を意味しているのでしょうか。
\(a\)は任意の定数\((a>0)\)です。そのため\(P(X≥a)\)というのは、\(a\)よりも大きい値のときの確率を指します。一方で右辺には期待値があります。つまり、期待値を\(a\)で割った値というのは、\(P(X≥a)\)よりも大きいことを意味します。
データを得るとき、期待値(平均)から大きく外れる値が出ることは珍しいです。これを数式で表しているのがマルコフの不等式です。任意の値\(a\)よりも大きい確率変数Xであっても、発生確率は期待値を\(a\)で割る値よりも必ず小さいのです。
マルコフの不等式を証明する
それでは、マルコフの不等式を証明してみましょう。高校数学で学ぶ積分を理解していれば、マルコフの不等式の証明が可能です。
連続型確率分布の場合、期待値\(E(X)\)というのは、確率密度\(f(x)\)(発生する確率)に対して確率変数X(\(x\))をかけることによって計算することができます。ただ連続型確率分布のグラフは曲線であるため、積分を利用して以下のように期待値を計算しましょう。
\(E(X)=\displaystyle \int_0^∞ xP dx\)
次に、任意の点\(a\)で面積を分けましょう。
\(\displaystyle \int_0^∞ xf(x) dx\)\(=\displaystyle \int_0^a xf(x) dx\)\(+\displaystyle \int_a^∞ xP dx\)
この積分というのは、\(\displaystyle \int_a^∞ xf(x) dx\)に比べて大きい値になります。
\(\displaystyle \int_0^a xf(x) dx\)\(+\displaystyle \int_a^∞ xf(x) dx\)\(≥\displaystyle \int_a^∞ xP dx\)
なお期待値の計算をするとき、\(x\)の値は増えていきます。例えばサイコロの目は1~6までの数があります。この場合、\(x\)の値は「1、2、3、4、5、6」と増えていきます。
一方で\(x\)の値を増やすのではなく、スタート地点の値\(a\)に固定する場合はどのようになるでしょうか。\(x\)の値を\(a\)に固定するため、以下の関係が成り立ちます(\(X>a\))。
\(\displaystyle \int_a^∞ xf(x) dx\)\(≥a\displaystyle \int_a^∞ f(x) dx\)
また確率密度では、面積を計算することによって発生確率Pを得ることができます。つまり、\(P=\displaystyle \int_a^∞ f(x) dx\)です。
\(a\displaystyle \int_a^∞ f(x) dx=aP(X≥a)\)
こうして、マルコフの不等式を証明することができました。
\(E(X)≥aP(X≥a)\):両辺を\(a\)で割る
\(P(X≥a)\)\(≤\displaystyle\frac{E(X)}{a}\)
確率論でのチェビシェフの不等式の証明
チェビシェフの不等式を証明するためには、先ほど解説したマルコフの不等式を利用します。まず、\(X=(X-μ)^2\)に変えましょう。どのようなケースであってもマルコフの不等式が成り立つため、確率変数Xを\((X-μ)^2\)へ変更するのは問題ありません。
また任意の数\(a\)を\(k^2σ^2\)に置き換えましょう。すると、以下の式になります。
\(P((X-μ)^2≥k^2σ^2)\)\(≤\displaystyle\frac{E((X-μ)^2)}{k^2σ^2}\)
なお\((X-μ)^2≥k^2σ^2\)が成り立つ場合、必ず\(|X-μ|≥kσ\)となります。そこで、以下のように式を直しましょう。
\(P(|X-μ|≥kσ)\)\(≤\displaystyle\frac{E((X-μ)^2)}{k^2σ^2}\)
また\(E((X-μ)^2)\)は分散の定義です。つまり、\(E((X-μ)^2)=σ^2\)です。そのため、以下のように計算できます。
\(P(|X-μ|≥kσ)\)\(≤\displaystyle\frac{σ^2}{k^2σ^2}\)
\(P(|X-μ|≥kσ)\)\(≤\displaystyle\frac{1}{k^2}\)
こうして、チェビシェフの不等式を得ることができました。マルコフの不等式を利用すれば、簡単なステップによってチェビシェフの不等式を証明できます。
チェビシェフの不等式の意味を理解し、証明を行う
統計学で学ぶ確率論の一つがチェビシェフの不等式です。数式を見ても内容を理解することはできないため、多くの人が意味を把握することなく教科書を読み進めていくことになります。
そこで、チェビシェフの不等式が何を意味するのか理解しましょう。確率変数Xに関係なく、すべての分布について、取りうる最大の確率を計算できるのがチェビシェフの不等式です。正規分布でなくても利用できるため、有用な公式です。
またチェビシェフの不等式を証明するとき、マルコフの不等式を利用します。そこでマルコフの不等式が何を意味しているのか学び、マルコフの不等式を証明できるようになりましょう。そうすれば、マルコフの不等式を利用してチェビシェフの不等式を証明できます。
確率論を学ぶとき、数式をみて理解するのはやめましょう。そうではなく、数式が持つ意味を理解すれば内容を把握できるようになります。






