分散と標準偏差：統計データのばらつきと変量の変換

統計学を学ぶとき、必ず学ばなければいけない言葉として分散（Variance）と標準偏差（Standard deviation）があります。データのばらつき（散らばり）を示すのが分散と標準偏差です。

ただ分散と標準偏差を学ぶとき、これらが何を意味しているのか理解している人は少ないです。例えば、分散と標準偏差を利用できるのはヒストグラムが左右対称のときのみです。また標準偏差を利用すれば、どの範囲にどれくらいの個数が含まれているのかすぐに判断できます。

また統計データによっては、後で数字を足したり、かけたりすることもあります。この場合、平均値や分散、標準偏差がどのように変化するのか理解しなければいけません。これを変量の変換といいます。

統計データを解析するとき、分散や標準偏差を出せるようになるだけでは意味がありません。それらの値が何を意味するのか学びましょう。そこで、分散・標準偏差の出し方や意味、統計でどう役立つのかを含めて解説していきます。

1 データのばらつき（散らばり）を表す指標が分散と標準偏差
- 1.1 平均や分散、標準偏差を使えるのは正規分布のみ
2 分散と標準偏差はヒストグラムの勾配を表す
- 2.1 分散で二乗する理由：二乗すると数字は必ずプラスになる
- 2.2 ほかの公式を利用し、分散を出す
3 分散の平方根が標準偏差になる
- 3.1 ヒストグラムでの標準偏差の意味
4 データへの足し算とかけ算による変量の変換
- 4.1 足し算・引き算による平均値や分散、標準偏差の変化
- 4.2 かけ算・割り算による平均値や分散、標準偏差の変化
5 ばらつきを表す分散と標準偏差

データのばらつき（散らばり）を表す指標が分散と標準偏差

統計データで重要な値として代表値があります。代表値には平均値や中央値、最頻値があります。ただ平均値がわかったとしても、意味のあるデータなのかどうかわかりません。同じ平均値であっても、例えば以下のヒストグラムでは様子が大きく異なるとわかります。

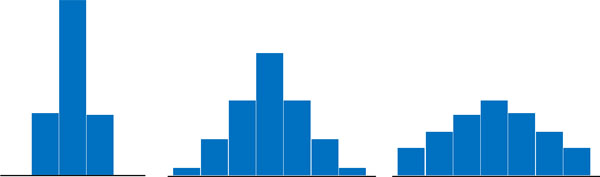
このように、グラフの形は大きく異なります。それぞれのデータがほぼ同じ値になる場合、ばらつきは小さくなります。例えば体温を測定する場合、ほとんどのケースで36℃代になります。つまり体温を測定すると、ばらつきは小さいです。

一方でそれぞれのデータの値が大きく異なる場合、ばらつきも大きくなります。例えば体重を測定する場合、人によって体重が大きく異なるため、ばらつきも大きくなります。体温のように、特定の値の周辺で測定結果を得られることはないからです。

この事実から、たとえ平均値が同じであっても、データのばらつきを考慮することが重要であるとわかります。そこでばらつきの度合いを示す指標として、分散と標準偏差が利用されるのです。

平均や分散、標準偏差を使えるのは正規分布のみ

なお分散や標準偏差を利用するときは注意点があります。それは、正規分布を示している統計データでのみ利用できることです。

ヒストグラムが左右対称の場合、正規分布しているグラフと判断できます。一方でグラフの左端（または右端）にある値が最も大きい場合、正規分布しているデータではありません。グラフの中に大きな山が2つ以上ある場合についても正規分布しているデータではありません。

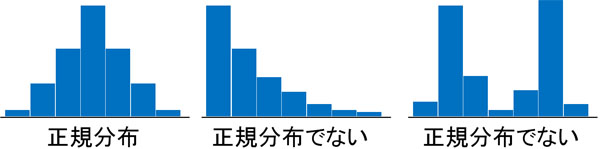
統計データで平均値が役立つのは、正規分布しているときのみです。正規分布していないデータでは、平均値を利用することはできません。正規分布していないデータで平均値を利用する場合、以下のようにデータ数の少ない場所が平均値になってしまいます。

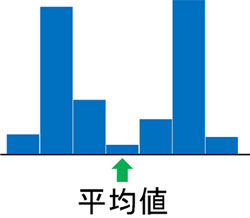
この場合、平均値を確認してもデータの形を正しく読み取ることはできません。これが、正規分布しているデータのみ、平均値が意味ある理由です。

なお分散と標準偏差は平均値を利用して値をだします。そのため平均値が意味ない値の場合、分散や標準偏差も意味がありません。これが、正規分布しているデータでない場合だと分散や標準偏差を利用できない理由です。

分散と標準偏差はヒストグラムの勾配を表す

それでは、分散と標準偏差は何を表すのでしょうか。データのばらつきというのは、どれだけグラフが左右に広がっているのかを示します。これはつまり、ヒストグラムの勾配を表しているのと意味が同じです。

データのばらつきが小さく、分散や標準偏差が小さい場合、ヒストグラムの勾配は大きくなります。一方でデータのばらつきが大きく、分散や標準偏差が大きい場合、ヒストグラムの勾配は小さくなります。

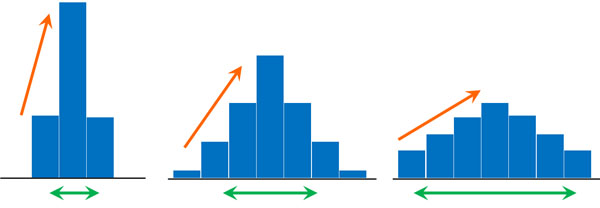
いずれにしても、このように分散や標準偏差はグラフの傾きに関与しています。

分散で二乗する理由：二乗すると数字は必ずプラスになる

それでは、どのようにしてデータのばらつきを出すのでしょうか。まずは分散の出し方を理解しましょう。データが正規分布している場合、平均値を利用することができます。

データによって、平均値からどれだけ値がずれているのか異なります。そこですべてのデータについて、平均値からのずれを計算します。平均値と比べてデータがどれだけずれているのかを知るためには、それぞれのデータから平均値を引けばいいとわかります。

例えば以下のデータについて、正規分布していると仮定して分散を求めてみましょう。

0, 6, -1, 3, 8, 2

先ほどのデータについて、平均値（Averege）は3です。そこでそれぞれのデータについて、3からどれだけずれているかを計算します。以下のようになります。

ただ、この状態では困ったことが起こります。平均値はすべてのデータを均一化した値です。そのため平均値からのずれを計算した後、すべて足すと必ず答えはゼロになります。つまりこの状態のまま計算すると、すべてのデータで分散がゼロになります。当然ながら、すべてのデータで分散がゼロなのは明らかにおかしいです。

平均値からの差を足すと合計がゼロになるのは、答えがプラスになったりマイナスになったりするからです。そこで平均値からの差を出した後、以下のように答えをプラスに変えましょう。

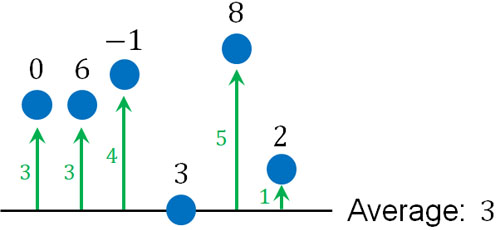
どのようにすれば、すべてのデータを自動的にプラスに変えることができるのでしょうか。プラスとマイナスが混ざっている場合、すべての数について二乗しましょう。そうすれば平均値との差がプラスであってもマイナスであっても、すべての値がプラスになります。

つまり分散を出すとき、平均値からそれぞれのデータを引いた後に二乗します。以下のようになります。

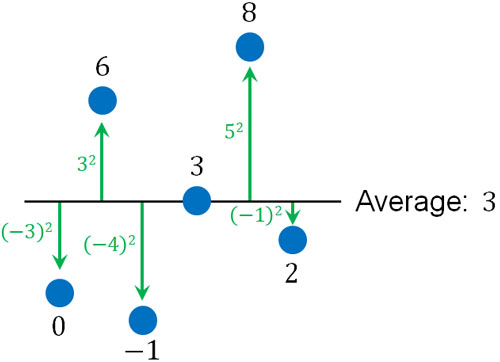
二乗する場合、すべての値がプラスになります。また二乗する場合、平均値との距離も反映されます。平均値との距離が大きいほど、二乗すると値が大きくなります。そこで分散を出すとき、以下のように平均との差をすべて足した後、データの個数で割りましょう。

\(\displaystyle\frac{(-3)^2+3^2+(-4)^2+5^2+(-1)^2}{6}=10\)

これによって、分散を出すことができます。参考までに、分散の公式は以下になります。

\(S^2=\displaystyle\frac{(x_1-\overline{x})^2+(x_2-\overline{x})^2+…+(x_n-\overline{x})^2}{n}\)

S²：分散
\(x_1\)や\(x_2\)など：それぞれのデータの値
\(\overline{x}\)：平均値
n：データの数

分散の公式を覚えても、何を意味しているのかわからず、利用することができません。統計学では、公式はどれも難しいです。そこで公式を覚えるのではなく、何を意味しているのか理解しましょう。そうすれば、公式を覚えなくても計算できるようになります。

統計データを扱う場合、コンピューターが計算してくれます。ただ試験問題を解く必要がある場合、分散の意味を理解して、公式を覚えなくても問題を解けるようにしましょう。

ほかの公式を利用し、分散を出す

なお分散を出すとき、ほかの方法を利用することによっても計算することができます。先ほどの公式を変形することによって、以下の公式を導き出すことができます。

\(S^2=\overline{x^2}-(\overline{x})^2\)

S²：分散
\(\overline{x^2}\)：「各データを二乗した値」の平均値
\((\overline{x})^2\)：平均値の二乗

この公式が成り立つ証明はしないものの、先ほど示した公式を展開することによってこの公式を作れます。なお先ほどのデータであれば、この公式を利用して以下のように分散を計算できます。

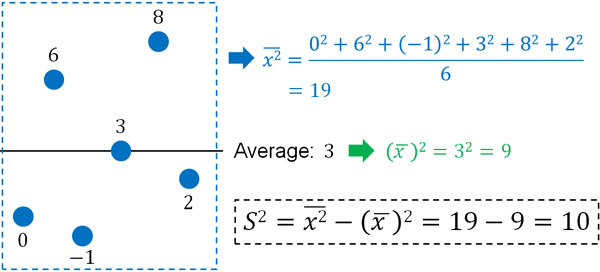
分散を計算するとき、「各データを二乗した後、平均化した値」と「平均値を二乗した値」を比べるとき、平均値を二乗するほうが数字は小さくなると予想できます。平均値は全体を均一化した値であるため、実際の各データを利用するほうが数字は大きくなるのです。

分散は数字を二乗するため、必ずプラスの値になります。大きい数字から小さい数字を引く必要があるため、先ほど記した公式を利用するためには、平均値の二乗（小さい値）を引けばいいとわかります。

分散の平方根が標準偏差になる

分散について理解した後、標準偏差を学びましょう。分散がわかる場合、標準偏差の出し方は簡単です。分散の平方根が標準偏差です。

例えば分散が10の場合、標準偏差は\(\sqrt{10}\)です。また分散が16の場合、標準偏差は4です。このように、ルートの記号を加えることによって標準偏差を出すことができます。

分散を出すとき、前述の通り「データと平均値の差」に対して二乗します。この場合、単位が合っていません。例えば距離の測定データについて、単位がcmの場合、二乗するとcm²になります。つまり距離ではなく、単位が面積になります。

そこで単位を元に戻すために標準偏差を利用します。数字を二乗しているため、平方根を利用することによって単位を戻すのです。平方根を利用すれば、cm²はcmになります。

分散はデータのばらつきを表します。同じように、標準偏差もデータのばらつきを表します。データの散らばりを示す指標としては、分散と標準偏差の2つがあると理解しましょう。

ヒストグラムでの標準偏差の意味

それでは、なぜ標準偏差を利用するのが重要なのでしょうか。この理由として、データが正規分布に従う場合、以下のようになるからです。

平均値から「標準偏差×1」の範囲：データ全体の68.3%
平均値から「標準偏差×2」の範囲：データ全体の95.5%
平均値から「標準偏差×3」の範囲：データ全体の99.7%

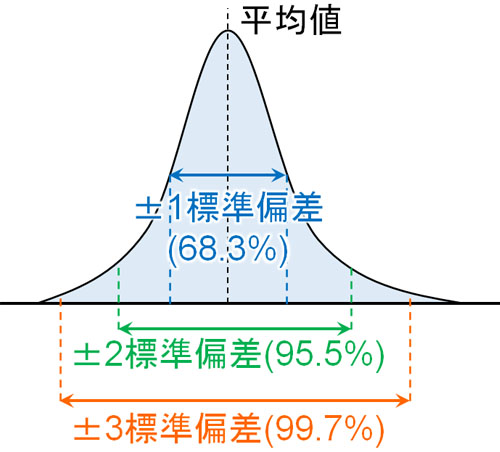
データが正規分布している場合、すべてのヒストグラムでこの関係が成り立ちます。標準偏差の大小に関係なくこの関係となるため、標準偏差を利用することによって得られたデータが何を意味するのか理解しやすくなるのです。

データへの足し算とかけ算による変量の変換

ここまでの内容を理解すれば、データへの足し算やかけ算を理解できるようになります。得られたデータについて、操作を加えることができます。例えばすべてのデータに対して数字を加えたり、数字をかけたりするのです。この場合、どのように平均値や分散、標準偏差が変わるのか理解しましょう。

統計データに対して足し算やかけ算をするとき、公式を利用してもいいです。ただ公式を覚え、数字を代入しても、それが何を意味しているのか理解していないと意味がありません。また応用問題が出されたとき、どのように解けばいいのかわかりません。

そこで公式を覚えるのではなく、統計データを操作することで値がどのように変化するのか考え方を理解しましょう。そうすれば公式を利用しなくても、統計データでの変量の変換を理解できるようになります。

なお先に結論を述べると、データに対して足し算（または引き算）をしたり、かけ算（または割り算）をしたりするとき、以下のように平均・分散・標準偏差が変化します。

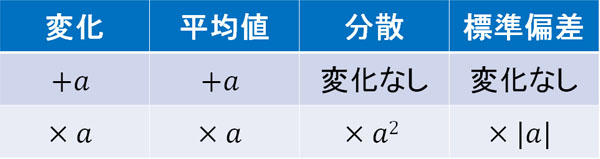
なぜ、このように変化するのでしょうか。

足し算・引き算による平均値や分散、標準偏差の変化

元のデータに対して足し算（または引き算）をするとは、つまりどういうことなのでしょうか。例えば、以下のデータがあるとします。

0, 6, -1, 3, 8, 2

このデータの平均値や分散、標準偏差は先ほど計算した通り以下のようになります。

平均値（Averege）：3
分散（Variance）：10
標準偏差（Standard deviation）：\(\sqrt{10}\)

一方、すべてデータに対して2を足すとどうなるでしょうか。先ほどのデータについて、2が加わるので以下のデータになります。

2, 8, 1, 5, 10, 4

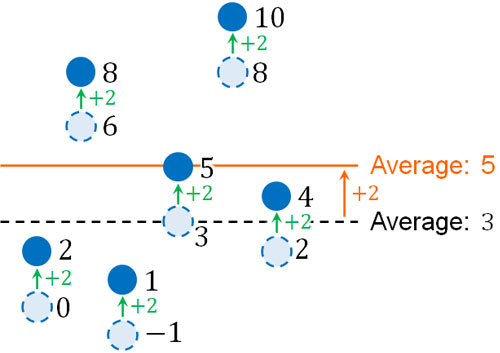
すべてのデータに2が加わっているため、平均値についても2増えると予想できます。全データを足した後、個数で割ると平均値を出すことができます。全データで2増えているため、当然ながら平均値も2増えるのです。

また全データの値が増えたとしても、データのばらつきは変化していません。データの場所は移動しているものの、それぞれのデータのばらつきは同じです。

データの散らばりが同じであるため、分散と標準偏差は変わりません。これが、データに対して数字を足したり、引いたりするときの分散と標準偏差の変化です。

例えば統計データ（変量\(x\)）について、以下のような新しいデータ（変量\(y\)）を作るとき、平均値や分散、標準偏差はどのように変化するでしょうか。

\(y=x-4\)

この場合、すべてのデータについて4引くことになります。そのため元の統計データ（変量\(x\))と比べて、新たなデータ（変量\(y\)）の平均値は4低いです。一方で分散と標準偏差は変わりません。

かけ算・割り算による平均値や分散、標準偏差の変化

次に、統計データに対してかけ算（または割り算）をするときの変量の変化を考えてみましょう。例えば全データに対して3倍したり、\(\displaystyle\frac{1}{4}\)倍したりするのです。先ほどと同じように、「0, 6, -1, 3, 8, 2」のデータを使いましょう。

平均値（Averege）：3
分散（Variance）：10
標準偏差（Standard deviation）：\(\sqrt{10}\)

例えば全データを2倍する場合、平均値や分散、標準偏差はどのように変化するでしょうか。以下のようになります。

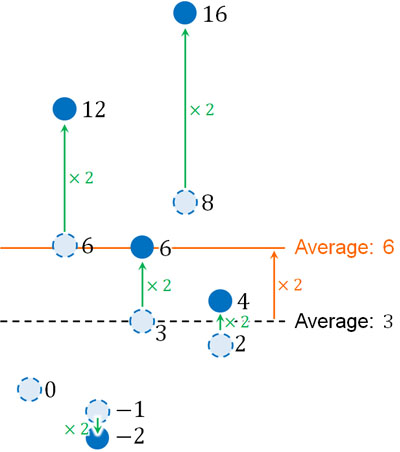
すべてのデータが2倍になるため、平均値についても2倍になると予想できます。例えばデータとしてa、b、cがある場合、すべてのデータに対して2倍するというのは、以下のように「すべてのデータを足した後に2倍する」のと意味が同じです。

\(a×2+b×2+c×2=2(a+b+c)\)

また平均値を出すとき、個数で割ることになります。データが2倍になっているため、平均値も2倍になります。

それでは、分散や標準偏差はどのように変化するのでしょうか。先ほどの図を確認してわかる通り、全データを2倍するとばらつきが大きくなります。

つまり分散が変化します。これまで解説した通り、分散を計算するときは二乗を利用します。そのため元のデータ（変量\(x\)）に対して2倍する場合、分散は\(2^2=4\)倍になります。\(a\)倍する場合、分散は\(a^2\)倍になるのです。

また標準偏差は分散の平方根であるため、全データを2倍すると、標準偏差は2倍になります。

なお分散は二乗によって正の値になるため、その平方根である標準偏差は必ず正の値になります。そのため例えばデータを-3倍する場合、\(|-3|=3\)となり、標準偏差は3倍になります。元のデータにマイナスの数字をかける場合、標準偏差が正の値になるようにかけ算をしましょう。

例えば統計データ（変量\(x\)）について、以下の新しいデータ（変量\(y\)）を作るとします。

\(y=-\displaystyle\frac{1}{3}\)

この場合、平均値や分散、標準偏差はどのように変化するでしょうか。\(-\displaystyle\frac{1}{3}\)倍することになるため、平均値は\(-\displaystyle\frac{1}{3}\)倍になります。

一方で分散は二乗することになるため、\(\left(-\displaystyle\frac{1}{3}\right)^2=\displaystyle\frac{1}{9}\)倍になります。また標準偏差は\(\left|-\displaystyle\frac{1}{3}\right|=\displaystyle\frac{1}{3}\)倍になります。

理由を理解すれば、公式を覚えなくても変量の変換をすることができます。統計学を学ぶとき、公式を覚えるのではなく意味を理解しましょう。