統計学で学ぶ検定方法の一つがフィッシャーの正確確率検定です。分割表を利用して確率を直接計算し、検定する方法がフィッシャーの正確確率検定になります。
データ数の少ないセルが含まれている場合、フィッシャーの正確確率検定は有効です。分割表の検定では基本的にカイ二乗検定を利用すればいいものの、フィッシャーの正確確率検定を利用することによって正確な確率を得ることができます。
それでは、フィッシャーの正確確率検定はカイ二乗検定と何が違うのでしょうか。また、どのように確率を計算すればいいのでしょうか。
確率を直接計算することで検定する方法はいくつか存在します。その一つがフィッシャーの正確確率検定であり、計算のやり方を解説していきます。
もくじ
フィッシャーの正確確率検定とカイ二乗検定の違い
検定方法の中でも、分割表を利用して検定する方法がフィッシャーの正確確率検定です。このとき、分割表を利用する検定法にはカイ二乗検定とフィッシャーの正確確率検定があります。
分割表を利用するため、以下の表についてフィッシャーの正確確率検定を行います。
| A1 | A2 | |
| B1 | ||
| B2 |
カイ二乗検定で分割表を利用するとき、独立性検定をします。つまり、それぞれのセルが独立しているかどうか(それぞれのセルで関連性があるかどうか)を調べることができます。フィッシャーの正確確率検定についても、独立性の検定が可能です。
つまりフィッシャーの正確確率検定もカイ二乗検定も同じ検定をしていると理解しましょう。両方とも独立性検定をすることによって、それぞれのセルについて関連性を調べることができるのです。
フィッシャーの正確確率検定とカイ二乗検定の違い
ただフィッシャーの正確確率検定とカイ二乗検定について、検定内容が同じとなると、両者は何が違うのでしょうか。両方とも、分割表を利用して独立性検定をすることができるものの、以下のような違いがあります。
- フィッシャーの正確確率検定:p値を直接計算する
- カイ二乗検定:カイ二乗値を利用して検定する
カイ二乗検定をする場合、カイ二乗値を計算することによって検定します。カイ二乗分布を利用し、有意水準と比べることで有意差を確認するのです。つまり、カイ二乗分布へ近似することによって確率を計算します。
一方でフィッシャーの正確確率検定では、カイ二乗分布に近似させることはしません。起こる確率を直接計算するのがフィッシャーの正確確率検定です。
二項検定とz検定の違いと同じと理解すればいい
フィッシャーの正確確率検定とカイ二乗分布の関係というのは、二項検定とz検定の関係と同じと理解しましょう。
二項検定では、結果が2つのケースで確率を直接計算します。例えばサイコロを6回投げ、1の目が4回出る確率は0.0080です。また、より極端なケースをすべて足すと確率は約0.00866(0.87%)です。
\(_6C_4\left(\displaystyle\frac{1}{6}\right)^4\left(\displaystyle\frac{5}{6}\right)^2≒0.0080\)
\(_6C_5\left(\displaystyle\frac{1}{6}\right)^5\left(\displaystyle\frac{5}{6}\right)^1≒0.00064\)
\(_6C_6\left(\displaystyle\frac{1}{6}\right)^6\left(\displaystyle\frac{5}{6}\right)^0≒0.000021\)
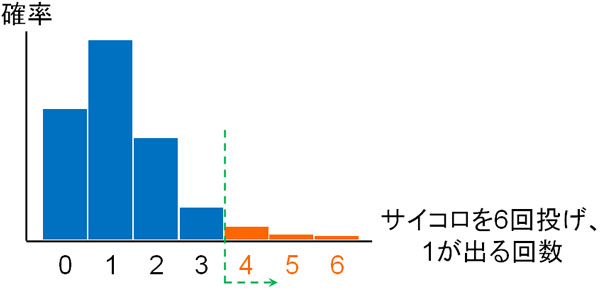
有意水準を0.05(5%)で考えると、起こる確率は0.00866(0.87%)であるため、5%以下で起こる稀なイベントが発生しています。そのため、この場合はサイコロにイカサマがあると判断できます。
一方、サイコロを1200回投げ、1の目が170回出た場合はイカサマがあるでしょうか。この場合、確率を直接計算するのは大変です。そこで正規分布へ近似させてp値を得ます。標準正規分布を利用して確率を計算し、有意差を判定する方法がz検定です。
二項検定は確率を直接計算し、z検定では正規分布へ近似させることによって有意差を判断します。同じように、フィッシャーの正確確率検定では確率を直接計算し、カイ二乗検定ではカイ二乗分布へ近似させることによって有意差を判断します。
一つのセルの値を確認し、使い分けをする
それでは、どのようなときにフィッシャーの正確確率検定を利用するべきなのでしょうか。一つの基準として、標本に含まれるデータ数のうち、「5以下のセル」が含まれる場合はフィッシャーの正確確率検定を利用するといいです。
例えば以下の場合、すべてのセルで値が5よりも大きいです。
| A1 | A2 | |
| B1 | 20 | 15 |
| B2 | 25 | 23 |
一方で以下の標本では、4つのうち1つのセルで値が5以下です(データ数4)。
| A1 | A2 | |
| B1 | 4 | 15 |
| B2 | 25 | 23 |
「少ない値を含むセル」の割合が20%以上の場合、フィッシャーの正確確率検定を利用するといいです(上図の場合、4セルのうち1つでデータ数の値が5以下のため25%)。
なぜ少ないデータ数を含む場合はフィッシャーの正確確率検定が優れているのでしょうか。近似によって確率を得る場合、データ数が多いほど正確です。一方、データ数が少ないと正しく確率を計算できず、結果として本来とは異なる検定結果になってしまうことがあります。そのため、データ数が少ない場合はフィッシャーの正確確率検定を利用します。
当然、フィッシャーの正確確率検定とカイ二乗検定では得られるp値が異なります。カイ二乗検定はあくまでも近似値であるため、正確な値ではないのです。そこで正確な値を直接得る方法がフィッシャーの正確確率検定です。
フィッシャーの正確確率検定を利用し、計算を行う
それでは、実際にフィッシャーの正確確率検定を利用して計算をしてみましょう。例えば以下の2×2分割表について、差はあるでしょうか。
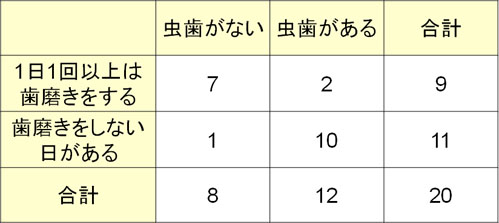
帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:歯磨きと虫歯に関連性はない
- 対立仮説:歯磨きと虫歯に関連性がある
差がない場合、歯磨きと虫歯に関係はありません。そこで、先ほど記した表について、起こる確率を直接計算し、有意水準と比べてみましょう。例えば、以下のセルに着目しましょう。
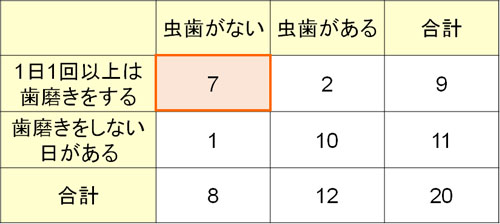
この結果が起こる確率はいくらでしょうか。
毎日、歯磨きをする人は合計で9人です。また、毎日歯磨きをしない人は11人です。つまり、合計20人です。この中から、虫歯がない人を8人選んでいきます。そこで、以下のように選びましょう。
- 毎日歯磨きをする人の中から虫歯がない人を7人選び、毎日歯磨きをしない人の中から虫歯がない人を1人選ぶ。
この場合、確率は以下のようになります。
\(\displaystyle\frac{_9C_7×_{11}C_1}{_{20}C_8}≒0.0031\)
このように確率を計算すると、今回の結果が起こる確率は0.0031(0.31%)とわかります。
極端なケースをすべて足し、確率を得る
なお検定をする場合、より極端なケースの確率についても計算しましょう。今回の例題であれば、以下の確率をすべて計算し、足すのです。
- 毎日歯磨きをする人の中から虫歯がない人を7人選び、毎日歯磨きをしない人の中から虫歯がない人を1人選ぶ。
- 毎日歯磨きをする人の中から虫歯がない人を8人選び、毎日歯磨きをしない人の中から虫歯がない人を0人選ぶ。
それぞれの確率は以下のようになります。
\(\displaystyle\frac{_9C_7×_{11}C_1}{_{20}C_8}≒0.0031\)
\(\displaystyle\frac{_9C_8×_{11}C_0}{_{20}C_8}≒0.000071\)
合計すると、今回の場合だと確率は先ほどと変わらず約0.0031(0.31%)です。このようにして、p値を得ることができました。
有意水準を0.05(5%)とすると、p値は0.0031(0.31%)であるため、非常に稀なイベントが起こっていると判断できます。そこで帰無仮説を棄却し、対立仮説を採用しましょう。つまり、歯磨きと虫歯には関係があると判断できます。
なお、今回の例題のようにサンプルサイズが少ない場合、直接計算することができます。一方でサンプルサイズが大きい場合、計算が大変になります。そのため、データ数が多い場合はカイ二乗検定を利用しましょう。
3群以上を計算するときの考え方
なおフィッシャーの正確確率検定について、3群以上であっても検定処理することができます。この場合は計算が非常に複雑になるため、統計ソフトを利用して判定しましょう。
なおデータ数が多い場合、フィッシャーの正確確率検定では計算が大変になるため、結果を得るまでに時間を要することがあります。ただ重要なのは、3群以上であってもフィッシャーの正確確率検定を利用できることです。
また2×2分割表での検定法を理解していれば、3群以上の標本を用いてフィッシャーの正確確率検定をするときについても、有意差を判定できるようになります。
p値を直接計算するのがフィッシャーの正確確率検定です。そこで0.05(5%)や0.01(1%)などの有意水準と比較し、差があるかどうかを判定すれば問題ありません。
p値を直接計算し、イベントの発生確率を計算する
分割表を利用して検定する方法の一つがフィッシャーの正確確率検定です。通常はカイ二乗検定を利用するものの、データ数の少ないセルが含まれている場合、確率を直接計算するほうが有用であるケースは多いです。
直接計算するため、計算過程は大変です。2×2分割表であれば確率の計算は難しくないものの、3群以上の場合は統計ソフトを用いてp値を出しましょう。
基本的にはカイ二乗値と性質は同じであり、独立性検定をするときにフィッシャーの正確確率検定を利用します。そこで、どのような場面で使い分けをすればいいのか特徴を理解しましょう。
フィッシャーの正確確率検定とカイ二乗検定の関係というのは、二項検定とz検定の関係に似ています。確率を直接計算するのか、それとも近似によって確率を得るのかが異なります。こうした特徴を理解して、フィッシャーの正確確率検定を利用しましょう。






