化学平衡：平衡定数の計算と圧平衡定数

化学反応は一方通行であることが多いです。つまり反応が起こり、生成物を生じたのであれば、それで反応が完了します。

ただ化学反応の中には、生成物から反応物へと逆向きの反応を起こすことがあります。この場合、反応物と生成物が混在することになります。こうしたとき、重要になる概念が化学平衡です。また化学平衡では、平衡定数を利用することで化合物の量を計算できます。

それでは、どのように化学平衡の計算をすればいいのでしょうか。化学平衡では平衡定数や公式の意味を理解する必要があります。

なお化学平衡では、圧力を利用する圧平衡定数も重要であるため、同時に理解しましょう。ここでは、化学平衡の概念や計算方法を解説していきます。

化学平衡では逆反応が起こる：不可逆反応と可逆反応

化学を学ぶとき、私たちが最初に学ぶのは不可逆反応です。不可逆反応としては、例えば燃焼反応や中和反応が挙げられます。これらの反応は一方方向のみ進行します。

例えば水素と酸素を反応させるとき、水が生成されます。ただ、水が勝手に水素と酸素に分解されることはありません。この反応は不可逆反応だからです。

一方、放置していると生成物の一部が反応物へと戻ることがあります。こうした化学反応として可逆反応があります。

化学平衡を学ぶとき、水素（H₂）とヨウ素（I₂）が反応し、ヨウ化水素（HI）が生成される化学反応が例としてひんぱんに利用されます。まず、ヨウ化水素が生成するときの反応（正反応）は以下になります。

• H₂ ＋ I₂ → 2HI

また、ヨウ化水素が生成したと同時に逆反応も起こります。つまり、以下の反応が起こります。

• 2HI → H₂ ＋ I₂

反応物から生成物が生まれるものの、このように生成物から反応物へと逆戻りすることもあります。そこで、通常は2つの反応を合わせて以下のように記載します。

• H₂ ＋ I₂ ⇆ 2HI

なお時間が経過すると、正反応と逆反応のスピードが同じになり、見かけ上は反応が停止しているようにみえます。この状態を平衡といいます。

化学平衡の式と平衡定数の意味

それでは、平衡状態を式で表すようにしましょう。例えば、以下の化学反応式があるとします。

• aA ＋ bB ⇆ cC ＋ dD

このとき、平衡状態を表すには以下の式を利用します。

• \(\displaystyle\frac{[C]^c[D]^d}{[A]^a[B]^b}=K\) （定数）

※[A]、[B]、[C]、[D]はモル濃度（mol/L）を表します。

温度が一定の場合、定数Kは必ず一つの値に決まります。このとき化学反応式の左側が分母になり、右側が分子になります。また、モル濃度の指数は化学反応式の係数と一致します。

例えば、以下の可逆反応を考えましょう。

• H₂ ＋ 3N₂ ⇆ 2NH₃

この場合、平衡定数Kを利用して以下のように式を表します。

• \(\displaystyle\frac{[NH_3]^2}{[H_2][N_2]^3}=K\) （定数）

分母・分子の位置と化学反応式の係数に着目して、平衡定数を用いた式を作りましょう。

化学反応での化学平衡の性質

それでは、平衡定数は何を意味しているのでしょうか。平衡定数が大きいというのは、分子の値が大きいことを意味しています。つまり平衡定数が1よりも大きい値の場合、化学反応は生成物側に偏ります。

一方、平衡定数が小さい場合、分母が大きいです。そのため平衡定数が1よりも小さい値の場合、化学反応は反応物側に偏ります。

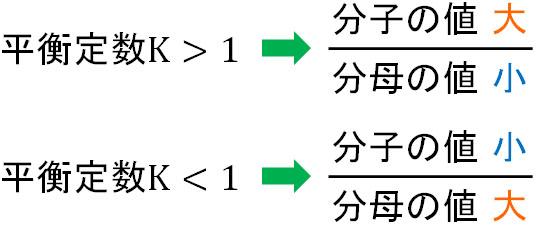
当たり前のことを述べているように思いますが、平衡定数を理解するとき、この概念を学ぶことが非常に重要です。平衡定数を確認すれば、化学反応が進行することによって、生成物を多く得られるのか、それとも反応物が多く残るのかがわかるのです。

物質が追加されると、時間をかけて平衡になる

それでは、物質が追加されるとどのようになるのでしょうか。例えば、平衡定数Kが1となる以下の反応を考えてみましょう。

• A ＋ B → C
• \(\displaystyle\frac{[C]}{[A][B]}=1\)

平衡定数が1というのは、分母と分子の値が同じであることを意味しています。そのため、必ず以下の関係が成り立たなければいけません。

• \([A][B]=[C]\)

例えば、1Lの容器にそれぞれの物質が1molずつあると\(1×1=1\)となります。それでは、容器の体積（1L）と温度を同じにして、物質Aを5mol追加したらどうなるでしょうか。この場合、平衡状態は以下のようになります。

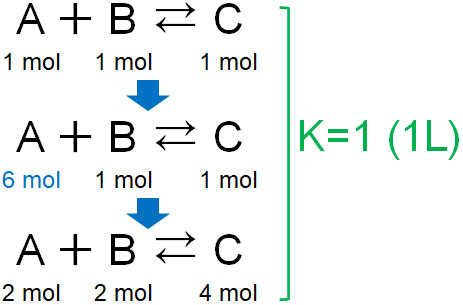
平衡状態では\(2×2=4\)であるため、K=1を満たしています。いずれにしても、平衡定数が同じになるように濃度が変化するのです。

なお触媒は平衡定数に影響しません。触媒は活性化エネルギーを低くすることにより、反応の進行をスムーズにします。触媒があると正反応と逆反応の両方の反応スピードが速くなるため、結果的に平衡定数は同じなのです。

化学平衡の計算方法：平衡定数を求める

それでは、実際に平衡定数を計算してみましょう。ここまで解説した内容を理解すれば、平衡定数の公式を利用することで化学平衡の計算をすることができます。

化学平衡での計算問題は主に以下の2種類です。

• 平衡定数を求める
• 平衡状態になるとき、生成物（または反応物）の物質量を計算する

まず、平衡定数の計算方法を解説していきます。平衡定数を求めるとき、化学反応式を作った後、それぞれの物質のモル濃度を計算しましょう。その後、平衡定数の公式に値をあてはめるといいです。

例えば、以下の問題の答えは何でしょうか。

• 3.0molの水素H₂と3.0molのヨウ素I₂を容器に入れ、温度一定で反応させると、ヨウ化水素が1.2mol生成されました。この温度での平衡定数Kを求めましょう。

温度が一定の場合、平衡定数は同じです。平衡定数を計算するため、以下の化学反応式を作りましょう。

• H₂ ＋ I₂ ⇆ 2HI

その後、反応後にH₂とI₂が何mol存在するのか確認します。以下のようになります。

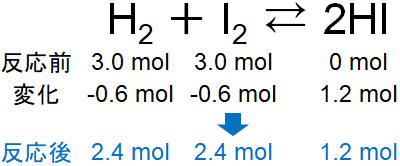
平衡状態では、反応後にいくらの物質量が存在するのかわかりにくいです。そこで、変化する量を計算しましょう。

ヨウ化水素が1.2mol生成するというのは、水素とヨウ素はそれぞれ0.6molずつ消費されることを意味しています。そこで引き算をすると、平衡状態での水素とヨウ素の物質量を計算できます。

反応後の物質量を計算したら、平衡定数Kを計算しましょう。以下の式によって平衡定数Kを得ることができます。

• \(\displaystyle\frac{[HI]^2}{[H_2][I_2]}=K\)

容積をVとすると、以下のように計算できます。

\(\displaystyle\frac{\left(\displaystyle\frac{1.2}{V}\right)^2}{\left(\displaystyle\frac{2.4}{V}\right)\left(\displaystyle\frac{2.4}{V}\right)}=K\)

\(K=0.25\)

こうして、公式を利用することによって平衡定数Kは0.25であるとわかりました。

平衡状態になるときの物質量を計算する

次に、平衡状態になるときの物質量を計算しましょう。以下の問題の答えは何でしょうか。

• 水素とヨウ素が反応すると、ヨウ化水素が生成されます。温度と容積を一定にして、空の容器に3molのヨウ化水素（HI）を追加しました。平衡状態に達した後、水素の物質量はいくらでしょうか。なお、平衡定数Kは0.25です。

水素の物質量を知りたいため、逆反応によって生成する水素の物質量を\(x\)molとしましょう。そこで、先ほどと同様にどのように値が変化するのか記します。反応後は以下のようになります。

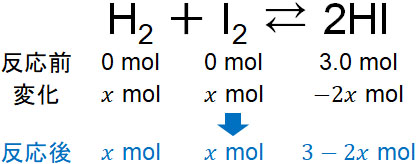
温度は一定であるため、平衡定数Kは0.25です。また容積をVとすると、以下のように計算できます。

\(\displaystyle\frac{\left(\displaystyle\frac{3 -2x}{V}\right)^2}{\left(\displaystyle\frac{x}{V}\right)\left(\displaystyle\frac{x}{V}\right)}=0.25\)

\(\displaystyle\frac{(3-2x)^2}{x^2}=0.25\)

\(4(9-12x+4x^2)=x^2\)

\(15x^2-48x+36=0\)

\(5x^2-16x+12=0\)

\((x-2)(5x-6)=0\)

こうして、\(x=2,\displaystyle\frac{6}{5}\)になります。ただヨウ化水素の物質量に着目すると\(3-2x>0\)であるため、\(x=2\)は不適です。そのため\(\displaystyle\frac{6}{5}=1.2\)molが正解です。

すべて気体の場合、圧平衡定数を利用できる

なお化学反応を起こすとき、溶媒に溶けている物質だけでなく、気体の状態で化学反応が進むこともあります。すべて気体の場合、圧平衡定数を利用できます。

ここまで、モル濃度を用いて平衡定数を計算しました。一方、反応物も生成物もすべて気体の場合、それぞれの気体の分圧を用いることで圧平衡定数を得ることができるのです。例えば、以下の反応があるとします。

• aA ＋ bB ⇆ cC ＋ dD

このとき、圧平衡状態を表すには以下の式を利用します。

• \(\displaystyle\frac{(P_C)^c(P_D)^d}{(P_A)^a(P_B)^b}=K_P\) （定数）

※P_A、P_B、P_C、P_Dは分圧（Pa）を表します。

モル濃度（mol/L）を分圧（Pa）に変えることで圧平衡定数K_Pを得ることができます。性質は平衡定数と同じであり、温度が一定の場合は圧平衡定数は同じ値になります。

圧平衡定数を用いた問題の解き方は、平衡定数を用いる方法と同じです。モル濃度の代わりに分圧を求め、圧平衡定数を用いて計算しましょう。

圧平衡定数を用いた計算

それでは、圧平衡定数が関わる計算をしてみましょう。気体の計算では、気体の状態方程式を利用することがよくあります。そのため圧平衡定数だけでなく、気体の状態方程式を利用して計算することも考えましょう。

例えば、以下の問題の答えは何でしょうか。

• 0.30molの四酸化二窒素（N₂O₄）を1Lの容器に入れると、二酸化窒素（NO₂）が発生しました。また、両方の物質量の合計は0.51molでした。温度が27℃で一定のとき、平衡定数と圧平衡定数を有効数字2ケタで求めましょう。なお、気体定数Rは8.3×10³Pa·L/(K·mol)です。

平衡定数については、ここまで解説した方法と同じように計算しましょう。まず、四酸化二窒素（N₂O₄）は以下のように二酸化窒素（NO₂）へ変化します。

• N₂O₄ ⇆ 2NO₂

二酸化窒素（NO₂）の発生量を\(x\)molとすると、以下のように反応後の物質量を計算できます。

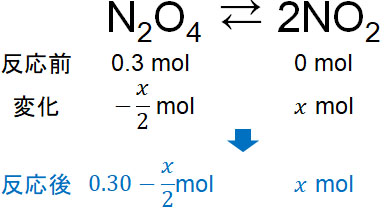
N₂O₄とNO₂の物質量を合計すると0.51molなので、以下のように計算できます。

\(0.3-\displaystyle\frac{x}{2}+x=0.51\)

\(x=0.42\)

こうして二酸化窒素（NO₂）の物質量は0.42mol、四酸化二窒素（N₂O₄）の物質量は0.090molになります。また容器1Lに入っているため、二酸化窒素（NO₂）のモル濃度は0.42mol/L、四酸化二窒素（N₂O₄）のモル濃度は0.090mol/Lです。

次に平衡定数の計算をすると、以下のようになります。

\(K=\displaystyle\frac{[NO_2]^2}{[N_2O_4]}\)

\(K=\displaystyle\frac{0.42^2}{0.09}\)

\(K=1.96\)

こうして、平衡定数Kは1.96になります。

・分圧を計算し、圧平衡定数を求める

なお圧平衡定数は分圧を利用します。そこで分圧を計算することによって答えを出しましょう。体積Vが1L、温度Tが300Kのときについて、気体の状態方程式を利用して分圧を計算しましょう。

二酸化窒素（NO₂）の物質量は0.42molであるため、分圧は以下のようになります。

\(P×1=0.42×R×300\)

\(P=126R\)

また四酸化二窒素（N₂O₄）の物質量は0.09molなので、分圧は以下のようになります。

\(P×1=0.09×R×300\)

\(P=27R\)

そこで、圧平衡定数の公式を利用して答えを得ましょう。

\(K_P=\displaystyle\frac{(P_{NO_2})^2}{P_{N_2O_4}}\)

\(K_P=\displaystyle\frac{(126R)^2}{27R}\)

\(K_P=588R\)

\(K_P=588×8.3×10^3\)

\(K_P≒4.9×10^6\)

こうして、圧平衡定数は4.9×10⁶になるとわかります。平衡定数と圧平衡定数は異なります。圧平衡定数の計算では、分圧を利用すると覚えましょう。

化学平衡の計算を行えるようにする

化学反応によっては平衡状態になることがあります。可逆反応の場合、平衡状態となります。温度が一定なのであれば、平衡定数は一定です。

そこで平衡定数Kを求めたり、生成物（または反応物）の物質量を計算したりできるようになりましょう。どれだけの量の化合物が変化したのか確認すれば、平衡定数の公式を利用することによって計算できます。

なお平衡定数を理解したら、圧平衡定数も学びましょう。平衡定数と圧平衡定数の計算方法は同じです。モル濃度を分圧に変えると、圧平衡定数の計算が可能になります。

化学平衡の計算問題は内容が複雑です。そこで反応前と反応後の化合物量を確認し、平衡定数を利用して計算を進めていきましょう。