カイ二乗分布を利用することによる検定方法としてカイ二乗検定があります。カイ二乗値(χ2値)を利用することによって、データが正しいかどうか判断したり、独立かどうかを判定したりすることができます。
データが理論値とずれているかどうかを調べるカイ二乗検定として適合度検定があります。適合度検定により、データにばらつきがあるかどうかを見分けられます。
またカイ二乗検定では、独立性検定も利用されます。独立性検定を利用することにより、「事象に関連性があるかどうか」を判断することができます。
カイ二乗検定はすべての統計学の教科書で記載されています。そこで、適合度検定や独立性検定の方法を解説していきます。
もくじ
予想される期待値とのズレをカイ二乗検定で確認する
なぜカイ二乗検定をする必要があるのでしょうか。カイ二乗検定とは、大まかに「分散(データのばらつき)を利用することによって検定する方法」と理解しましょう。データにばらつきがあることを判断できれば、例えばイカサマがあるかどうか判断できます。
例えばサイコロを投げるとき、通常であれば1~6の数字が出る確率はそれぞれ\(\displaystyle\frac{1}{6}\)です。そのためサイコロを投げるとき、出る目の期待値(平均)は3.5です。
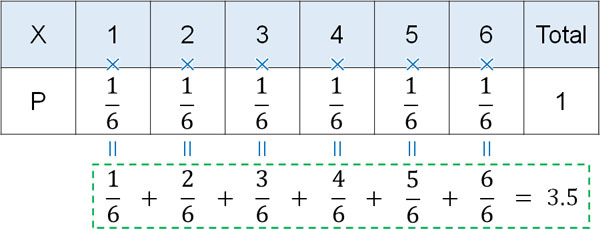
一方でサイコロに細工をすると、出る目が異なります。例えばサイコロを30回投げ、以下の結果になったとします。
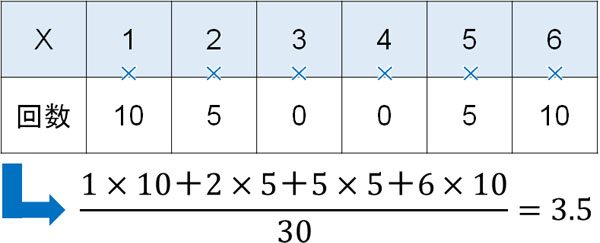
この結果についても、期待値は3.5です。そのためサイコロに細工がない場合と比較して、期待値は合致しています。
ただ普通に考えて、この結果ではサイコロに何か細工があると考えるのが自然です。ただ平均値は3.5であり、一般的なサイコロの期待値と値が同じです。それではどのようにすれば、サイコロに細工があると判断すればいいのでしょうか。
このようなとき、カイ二乗検定を利用しましょう。適合度検定をすることによって、データのばらつきが理論値とずれているかどうかを判断できます。
適合度検定により、理論値とのズレを検証する
理論値とのズレを確認する方法としては、分散(または標準偏差)が頻繁に利用されます。データのばらつきを表すのが分散と標準偏差です。たとえ平均(期待値)が理想的な値と一致していたとしても、ばらつきが大きい場合、明らかにデータが変(不自然)といえます。
一般的なデータであれば、以下のような正規分布となります。
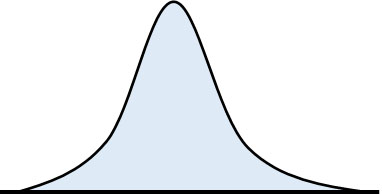
一方で平均値が同じであったとしても、以下のグラフであれば明らかにおかしいとわかります。
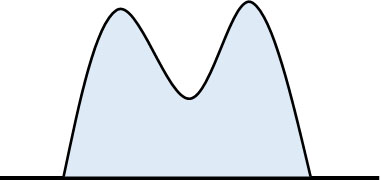
また、こうような形のグラフでは分散や標準偏差の値は大きくなります。そこでデータのばらつきを確認し、理論値とのズレを確認するのがカイ二乗検定です。
ピアソンのカイ二乗検定の公式
なお最も一般的なカイ二乗検定としてピアソンのカイ二乗検定があります。適合度検定や独立性検定はピアソンのカイ二乗検定によって可能です。
また、ピアソンのカイ二乗検定はグラフの形に関係なく利用できます。正規分布かどうかに関係なく利用できる検定法をノンパラメトリック検定といいます。ピアソンのカイ二乗検定というのは、ノンパラメトリック検定の一種です。
・カイ二乗検定の公式を得る
それでは、実際にカイ二乗値(χ2値)を得るための公式を作りましょう。カイ二乗値の計算では、一般的な分散とは計算方法が異なります。
まずそれぞれの値について、帰無仮説(差がない場合)での期待度数\(E\)を利用し、実際の観測値\(O\)から引き、二乗しましょう。
- \((O-E)^2\)
ばらつき(分散)の計算をする場合、一般的にはそれぞれの値について期待値を引き、二乗する必要があります。そのため、この計算については問題ないと思います。
次に、データごとの補正をしましょう。例えばコインを100回投げて表が80回出る場合、理論値(表50回)とのズレは30回です。一方でコインを1000回投げて表が530回出る場合、理論値(表500回)とのズレは30回です。
理論値とのズレは同じ30回です。ただ「コインを100回投げて表が80回出る場合」のほうが、明らかに結果がおかしいと判断できます。つまりデータの大きさによって、値が変かどうか違ってくるのです。
そこで、すべてのデータを標準化しましょう。具体的には、期待度数\(E\)と実際の観測値\(O\)の差を二乗した後、期待度数\(E\)で割ります。
\(\displaystyle\frac{(O-E)^2}{E}\)
データによって理論的な期待度数が異なります。つまり、グラフの横幅が異なります。そこで期待度数\(E\)で割ることにより、すべてのデータについて、どれだけ期待度数からのずれがあるのか客観的に判断できるようになります。
例えばデータとして\(O_1\)、\(O_2\)、\(O_3\)があるとき、カイ二乗値を以下のように計算します。
\(χ^2=\displaystyle\frac{(O_1-E)^2}{E}\)\(+\displaystyle\frac{(O_2-E)^2}{E}\)\(\displaystyle\frac{(O_3-E)^2}{E}\)
数学では、すべて足し算することを\(Σ\)で表します。そのため、適合度検定の公式は以下のように表されることが多いです。
- \(\displaystyle\sum{\displaystyle\frac{(O-E)^2}{E}}\)
これは、それぞれのデータについて\(\displaystyle\frac{(O-E)^2}{E}\)を計算したあと、すべて足すことを意味します。
・なぜ期待度数で割るのか
それでは、なぜ期待度数で割るのでしょうか。カイ二乗分布を学ぶとき、カイ二乗値の計算では「標準確率分布の確率変数を二乗して足す」と習います。以下が標準確率分布の確率変数\(Z\)を出すための公式です。
\(Z=\displaystyle\frac{X-μ}{σ}\)
\(X\)は実測値\(O\)のことであり、母平均\(μ\)は期待度数\(E\)とほぼ意味が同じです。そのため以下のように式を変えることができます。
\(Z=\displaystyle\frac{O-E}{σ}\)
ただ確率変数\(Z\)を二乗する場合、以下の式になります。
\(Z^2=\displaystyle\frac{(O-E)^2}{σ^2}\)
そのため、\(\displaystyle\frac{(O-E)^2}{E}\)と比較すると明らかに式が異なります。本来であれば分散\(σ^2\)で割る必要があるのに、適合度検定でカイ二乗値を出すときは期待度数\(E\)で割るのです。
それではなぜ、期待度数で割ってもいいのでしょうか。難しい数学の計算が必要になるため詳細は省きますが、「帰無仮説の場合、試行回数\(n\)が多くなるのであれば、\(\displaystyle\frac{(O-E)^2}{E}\)の式は近似的に自由度\(n-1\)のカイ二乗分布に従う」ことがわかっています。
統計学的な検定をする場合、必ず帰無仮説(データに差がない)という前提で検証します。そのためカイ二乗検定をするとき、期待度数で割っても近似的にカイ二乗値を計算できるため、これを利用するというわけです。
帰無仮説・対立仮説と自由度を利用して適合度検定を行う
それでは、実際に適合度検定をすることによってデータのばらつきに異常があるかどうかを確かめてみましょう。例題として先ほど述べたサイコロについて、細工があるかどうかを確かめましょう。
以下のように、まずは帰無仮説と対立仮説を立てます。
- 帰無仮説:サイコロに細工はない
- 対立仮説:サイコロに細工がある
まず適合度検定をするため、先ほどのサイコロの問題について以下のような表を作りましょう。
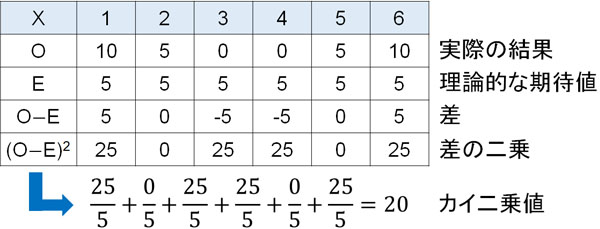
このようにして、カイ二乗値(χ2値)を計算することができました。
次は有意水準0.05となるカイ二乗値と比較することになります。今回の例題では、サイコロを投げるとき、母平均などの値は既にわかっています。またサイコロは1~6の目があり、自由度は\((6-1=)5\)です。そこで自由度5のとき、有意水準0.05のカイ二乗値を確認すると11.071です。
つまりカイ二乗値が11.071より大きい場合、5%以下の確率で発生する稀なケースが発生していると判断できます。先ほど計算したカイ二乗値は20であり、11.071よりも大きいです。そのため帰無仮説を棄却し、対立仮説を採用します。つまり、サイコロに細工があったと判断できます。
適合度検定を利用すれば、イカサマがあるかどうかを含め、理想的な値よりもどれだけズレているのか客観的に証明できます。
表を利用してデータの独立性を確かめる
次に、独立性検定を学びましょう。カイ二乗検定を利用することによって、事象が独立かどうかを確認することができます。
統計学において、事象が独立とはどういう意味なのでしょうか。事象が独立の場合、それぞれの事象には関連性がありません。一方で帰無仮説(事象は独立)が否定される場合、対立仮説を採用して「事象は独立ではない」と判断します。
事象が独立ではないというのは、つまり「2つの事象には互いに関連性がある」と結論付けることができます。独立性検定というのは、「それぞれの事象に関連性があるかどうか」を確認するための検定でもあるのです。
独立性検定によって差がない(独立である)と判断できる場合、事象に関連性はありません。一方で差がある(独立ではない)と判断できる場合、事象に関連性があるというわけです。
なお独立性検定では2×2分割表が頻繁に利用されます。母集団を属性Aと属性Bに分けることができる場合、四つの区分に分類できるのです。
| A1 | A2 | |
| B1 | ||
| B2 |
例えば、母集団に属性A(虫歯がない、虫歯がある)と属性B(1日1回以上は歯磨きをする、歯磨きをしない日がある)があるとします。そこで、調査結果をもとにして以下のような表を作ります。
| 虫歯がない | 虫歯がある | |
| 1日1回以上は歯磨きをする | 100 | 30 |
| 歯磨きをしない日がある | 20 | 50 |
この結果のとき、独立性検定をすることによって「歯磨きと虫歯が独立かどうか(関連性があるかどうか)」を調べることができます。
2×2分割表で独立性検定をするときの公式と期待度数、自由度
なお独立性検定をするとき、先ほど解説した公式と同じ公式を利用します。そこで、帰無仮説(差がない)のときの理論的な期待度数を計算しましょう。なお、帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:歯磨きと虫歯に関連性はない
- 対立仮説:歯磨きと虫歯に関連性がある
このとき2×2分割表で期待度数を計算するためには、どのようにすればいいのでしょうか。分割表には列と行があるため、両方を考慮しなければいけません。そこで、2つの要素を考慮した期待度数を計算しましょう。
独立性検定では、以下のようにして期待度数を計算します。

先ほどの表を利用して期待度数を計算すると、以下のようになります。
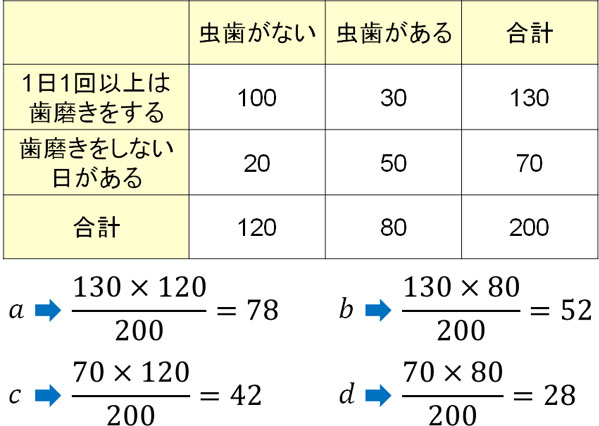
こうして期待度数が以下のようになると計算できました。
| 虫歯がない | 虫歯がある | |
| 1日1回以上は歯磨きをする | 78(期待度数) | 52(期待度数) |
| 歯磨きをしない日がある | 42(期待度数) | 28(期待度数) |
なぜ、このようにして期待度数を計算できるのかについては、理論を詳しく学びたい人のみ統計学の教科書を利用して学ぶようにしましょう。難しい計算が必要になるため、カイ二乗検定ができれば問題ない場合、このようにして期待度数を計算できることを理解できれば問題ありません。
次に、\(\displaystyle\sum{\displaystyle\frac{(O-E)^2}{E}}\)を利用することによってカイ二乗値を計算してみましょう。以下のようになります。
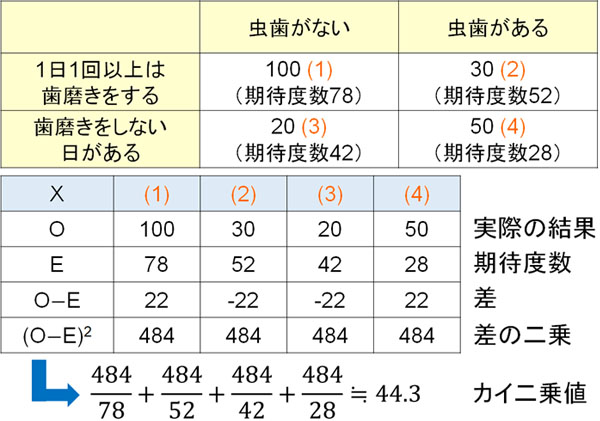
こうして、さきほどと同じ公式を利用することでカイ二乗値を計算することができました。
それでは、自由度はいくらになるのでしょうか。適合度検定と独立性検定では、自由度の出し方が異なります。独立性検定では分割表を利用することになり、以下の方法によって自由度を出しましょう。
![]()
2×2分割表の場合、列の数は2つです。また行の数は2つです。そのため、自由度は1です。
\((2-1)×(2-1)=1\)
つまり2×2分割表では、必ず自由度は1になります。それでは、自由度1のときに有意水準0.05となるカイ二乗値はいくらでしょうか。カイ二乗分布表を確認すると、カイ二乗値が3.841のとき、カイ二乗分布で上側確率が5%になります。
そこで\(P=0.05\)となるカイ二乗値3.841と先ほどのカイ二乗値44.3を比較すると、有意水準よりも値が大きいとわかります。5%以下の確率で起こる稀な事象が発生しているため、帰無仮説を棄却して対立仮説を採用しましょう。つまり、歯磨きと虫歯に関連性があると判断できます。
2×2分割表での独立性検定の簡易版公式
なお2×2分割表を用いる独立性検定では、簡易版の公式を利用することによってカイ二乗値を計算することもよくあります。簡易版の公式のほうが計算は簡単です。
簡易版の公式では、列と行についてそれぞれ合計値を計算しましょう。そうすると、以下の公式によってカイ二乗値を計算できます。
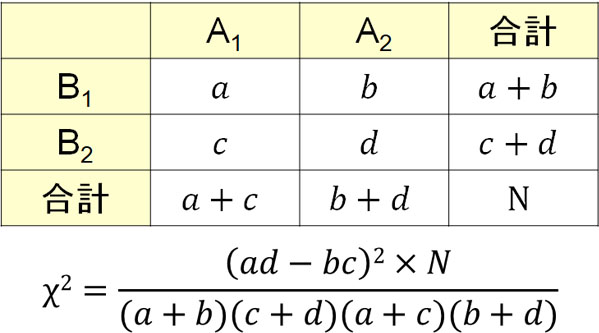
例えば先ほどの問題だと、以下のようにカイ二乗値を計算できます。
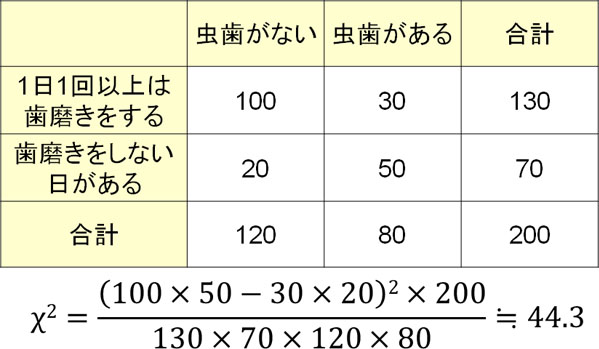
公式の形は異なるものの、同じ計算をしているため、当然ながらカイ二乗値の結果は同じです。ただ2×2分割表のカイ二乗値を計算するとき、この方法のほうが素早くカイ二乗値を得ることができます。
行や列が多いときの独立性検定の方法
ここまで、2×2分割表を利用して独立性検定をする方法を説明しました。それでは、より多くの列と行をもつ表について、どのように独立性検定をすればいいのでしょうか。
2×2分割表では、期待度数\(E\)を利用することによってカイ二乗値を計算しました。同じように\(\displaystyle\sum{\displaystyle\frac{(O-E)^2}{E}}\)の公式を利用することによって期待度数\(E\)を計算し、カイ二乗値を求めましょう。
例えば、以下の問題の答えは何でしょうか。
- 3つの工場で生産された製品について、一ヵ月に作られた不良品の数が以下になります。工場と生産される不良品数に関連性はあるでしょうか。
| 製品A | 製品B | 製品C | 合計 | |
| 工場A | 32 | 10 | 6 | 48 |
| 工場B | 27 | 15 | 8 | 50 |
| 工場C | 30 | 20 | 4 | 54 |
| 合計 | 89 | 45 | 18 | 152 |
分割表を利用する場合、「各セルの期待度数と観測値の差を二乗し、足すとカイ二乗分布に近似できる」という性質があります。そのため、この性質を利用することによってカイ二乗値を計算しましょう。また列と行が少ない2×2分割表についても、同様の性質によってカイ二乗分布を利用できるというわけです。
前述の通り、自由度は列の数と行の数に着目しましょう。先ほどの問題では、列の数は3です。また行の数は3です。そのため自由度は4です。
\((3-1)×(3-1)=4\)
なお、帰無仮説と対立仮説は以下になります。
- 帰無仮説:工場と製品の不良品数に関連性はない
- 対立仮説:工場と製品の不良品数に関連性がある
まずはそれぞれの期待度数を計算しましょう。以下のようになります。
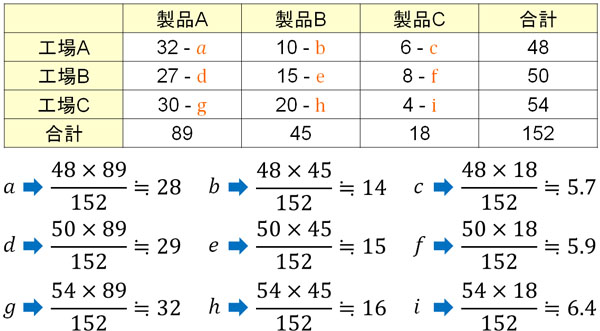
そこでカイ二乗値を計算すると以下のようになります。
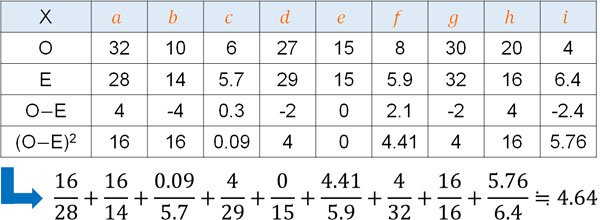
また自由度4のとき、カイ二乗分布で有意水準0.05となるカイ二乗値は9.488です。そのためカイ二乗値が9.488よりも大きい場合、5%以下で起こる稀な現象が発生しています。
ただ先ほど計算したカイ二乗値は4.64であり、9.488よりも小さい値です。そのため偶然に発生した事象と考えることができ、帰無仮説を棄却することができません。そのため工場と不良品数に関連性はなく、互いに独立しています。
計算過程は多くなるものの、計算方法や利用する公式は2×2分割表と同じです。列や行の数が多くなったとしても、独立性検定を行えるようにしましょう。
カイ二乗分布を利用し、適合度検定や独立性検定を行う
カイ二乗分布を学んだあと、カイ二乗検定を理解しましょう。カイ二乗値の計算をするとき、特に有名なのがピアソンのカイ二乗検定です。適合度検定や独立性検定はピアソンのカイ二乗検定に含まれます。
利用する公式はカイ二乗分布で学ぶときと少し異なります。ただ帰無仮説の場面を想定する場合、期待度数\(E\)と観測値\(O\)を利用することによって、近似的にカイ二乗分布に従います。そこでこの性質を利用し、カイ二乗検定をしましょう。
なお適合度検定と独立性検定では、自由度の求め方が異なります。利用する公式は同じであるものの、自由度の計算方法が異なるため、どのように自由度を得ればいいのか理解しましょう。
ピアソンのカイ二乗検定は頻繁に利用され、その中でも特に重要なのが適合度検定と独立性検定です。これらの方法を理解し、検定を行えるようになりましょう。