多くの因子によって結果を生じているとき、何が原因であるのか突き止めると将来の結果を予測できるようになります。
どの要因が結果に影響しているのか解析する手法はたくさんあり、その一つが因子分析です。因子分析によって共通点を見つければ、何が原因なのか把握できます。
ただ因子分析をするとき、どのような仮説を置くのかによって結果は変わります。つまり因子分析をすることによって、共通因子(関係のある因子)が何なのか明確にわかることはありません。人によって仮説は違うため、結果として結論が異なることがひんぱんに起こるのです。
因子分析は原因を探す方法として多くの人が利用しています。ただメリットだけでなく、デメリットも理解しましょう。そこで、どのように因子分析をすればいいのか基本的なポイントを解説していきます。
もくじ
因子分析では共通因子を発見できる
因子分析では、データに共通して存在する因子(共通因子)を見つけることを目的としています。一つの結果というのは、多くの要因によって成り立っています。そこで、具体的にどのような要因によって結果を得られているのか分析するのです。
因子分析でひんぱんに利用される例が教科です。数学・理科・英語・社会・国語のテストをすると、人によって点数に違いが表れます。このとき、以下の2つの傾向を発見できることは多いです。
- 数学と理科の点数は良いが、ほかの教科の点数は悪い
- 英語と社会と国語の点数は良いが、ほかの教科の点数は悪い
得られるデータはテストの点数です。ただ「数学の点数が良い場合、理科の点数も高い」という傾向があるケースは多いです。この場合、共通因子として理系と文系があります。
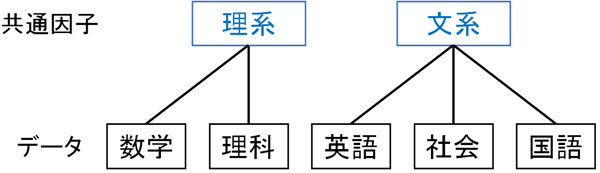
理系の人は一般的に数学と理科の点数が高いです。一方、文系の人は一般的に英語・社会・国語の点数が高いです。つまり、教科によって相関があるのです。因子分析では、こうした共通因子を見つけることができます。
共通因子・独自因子の概念と相関
次に、因子分析では「共通因子がどれだけ影響しているのか」を調べます。例えば理系学生の場合、一般的に数学と理科が得意です。ただ数学が得意だからといって、必ずしも理科が得意とは限りません。
共通因子によって、変数(今回の場合は数学や理科など)との相関の強さが異なります。このとき、例えば以下のように表すことができます。
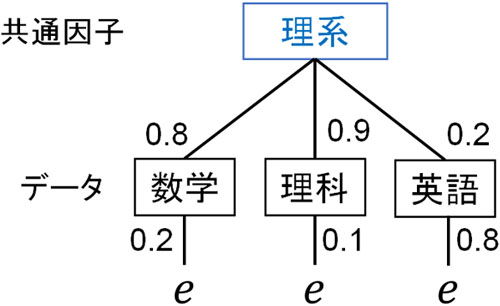
この場合、理系であることと数学との相関関係は0.8と強いです。ただ、理系だからといって必ずしも数学が得意とは限りません。そのため、独自因子(その他の因子:e)が存在します。この場合、以下のように表すことができます。
- 数学=理系の能力×0.8+e(0.2)
この式では、理系の能力が高いほど数学が得意です。ただ、「図形への理解」「空間の把握能力」なども数学で高得点を取るためには重要です。そこで、こうした独自因子としてe(今回は0.2)が存在するというわけです。
理科についても同様であり、先ほどの例であれば以下の計算式になります。
- 理科=理系の能力×0.9+e(0.1)
この結果の場合、数学に比べて、理系の能力が高いほど理科の高得点に結びつきやすいです。それに加えて、「自然科学への興味」などの独自因子eが重要になります。
一方で英語については、理系の能力との相関関係は低いです。そのためこのような結果の場合、英語で優れた点数を取るためには他の要素が深く関与しているとわかります。
いずれにしても、共通因子と独自因子を利用することによって相関関係を数値化すれば、どれくらい共通因子(または独自因子)の影響を受けるのか把握できます。
複数の共通因子が結果に関与することは多い
なお、複数の共通因子の影響を受けるケースは多いです。先ほどの例であれば、共通因子として理系と文系があります。つまり、2つの因子の影響を受けることは普通です。
例えば、以下の3パターンを考えてみましょう。
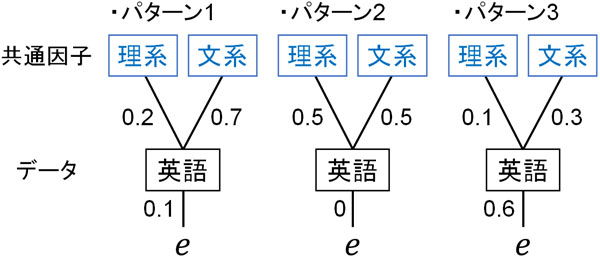
パターン1の結果を得られた場合、英語で高い点数を取るためには文系の能力が重要であることがわかります。一方で理系の能力はそこまで必要ではありません。
一方でパターン2の結果だと、英語の点数を取るためには理系の能力と文系の能力の両方が必要になります。数学や理科、社会、国語とあらゆる教科で高得点を取れる場合、英語の得点も高いです。
それに対して、パターン3は独自因子の影響が強いです。つまり理系の能力が高くても、文系の能力が高くても、英語の点数には大きな影響はありません。この場合、ほかの教科にはない英語特融の因子が重要になります。
因子分析では複数の要因を解析することになります。そこで、複数因子との相関関係や独自因子との関係を確認することで、因子同士がどのように影響し合っているのか把握することができます。
どの因子が影響しているのか発見するため、仮説を立てる
ただ実際のところ、因子分析をしたとしても、どのような因子が隠れているのか完ぺきに言い当てることはできません。
例えば「理系の能力が高い場合、数学と理科の点数が高い」ことがわかったとします。それでは、理系の能力とは何でしょうか。非常にあいまいであり、多くの人は説明することができません。
そこで、具体的にどのような因子が影響しているのか発見するために仮説を立てましょう。例えば、理系の能力を測るために以下のような項目をいくつか用意します。
- 計算スピードの速さ
- 論理的な思考能力
- 新たなアプローチ法を発見する独創力
こうした複数の要素が積み重なることによって理系の能力が高くなります。つまり、「理系の能力」というあいまいな概念の代わりとして、共通因子をより細分化するのです。
実際のところ、理系の能力というのは具体的に何を表しているのかわかりません。そこで因子分析では、何の因子が結果に影響しているのかあなたが仮説を立てて検証しなければいけません。
仮説によって結果が変化する
なお当然ながら、どのような仮説を立てるのかは人によって異なります。つまり因子分析をする場合、人によって結果は大きく変化します。
データを利用して相関関係を得るとき、表計算ソフトを利用して相関係数を得ます。この相関係数は誰であっても同じ答えを得ることができます。
ただ因子分析では、相関を得られた後に「どのような共通因子が存在するのか」をあなたが考え、仮説を立てる必要があります。当然、「どのような共通因子を想定するのか」は人によって大幅に異なります。これが、人によって因子分析をするときの結果が変わる理由です。
本来、統計解析をするときは人間の主観を排除しなければいけません。ただ因子分析では、必ず人の主観が入ってしまいます。バイアスが大きいため、因子分析を用いて共通因子を見つけるとき、ほかの統計手法に比べて正確性は非常に低いです。
また因子分析により、共通因子として「理系の能力や文系の能力」があるとわかったとしても、「確実に理系因子や文系因子が存在する」というわけではありません。因子分析というのは隠れた因子を明確に発見できる方法ではなく、データの特性を要約するために因子を利用するにすぎません。
探索的因子分析と確認的因子分析の違い
なお、因子分析には探索的因子分析と確認的因子分析があります。探索的因子分析とは、直接観察できない因子(潜在変数)をデータから見つけ出す方法です。これまで説明してきた方法が探索的因子分析になります。
一般的に、因子分析は探索的因子分析を指します。自ら仮説を設定し、得られたデータに存在する共通因子を見つけ出すのです。
前述の通り、探索的因子分析で共通因子を発見したとしても、共通因子が確実に存在するかどうかは不明です。あくまでも、共通因子はデータの補足にすぎません。
ただ得られた共通因子が正しいかどうかわからないとなると、利用する価値がありません。そこで、別のデータを用いて結果に整合性があるかどうか確かめる手法が確認的因子分析です。
探索的因子分析では仮説なしにデータを解析し、共通因子に何があるのかあなたが考えます。一方で確認的因子分析では、データを取った後、先に共通因子(仮説)を設定して解析を行います。これにより、仮説が正しいかどうかを検証することができます。
2つの相関関係をすべて確認する
それでは、実際に探索的因子分析をしてみましょう。因子分析をする簡単でわかりやすい方法としては、2つの相関関係をすべて確認するやり方があります。
例えば5種類のワインについて、プロのソムリエが試飲して点数を付けた結果、以下のようになったとします。
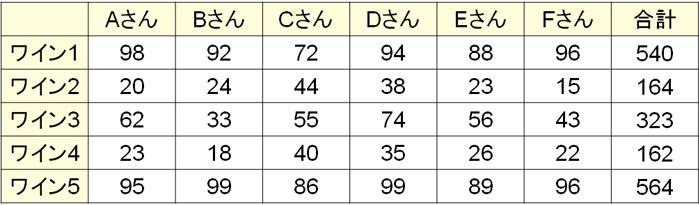
そこで、ワインごとの相関関係をそれぞれ確認しましょう。「ワイン1とワイン2の相関関係」「ワイン1とワイン3の相関関係」のように、一組ずつ相関係数を計算するのです。
実際の計算は表計算ソフトが行うことになり、以下は先ほどの表に関する相関関係の結果です。
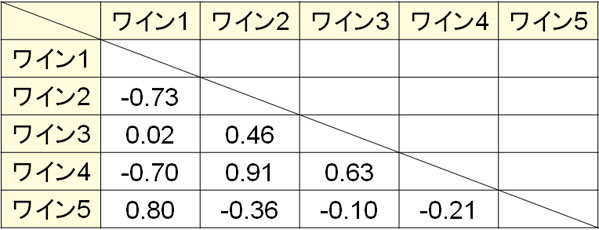
このように確認すると、以下の関係があるとわかります。
- ワイン1とワイン5:強い正の相関(0.80)
- ワイン2とワイン4:強い正の相関(0.91)
- ワイン1とワイン2:負の相関(-0.73)
- ワイン1とワイン4:負の相関(-0.70)
- ワイン3とワイン4:正の相関(0.63)
それぞれのワインについて相関係数を計算すれば、ワインごとの関係性を理解できるようになります。
因子ごとに特徴を記し、共通点を見つける
次に共通因子を考えましょう。どのような共通因子を思いつくのかは人によって異なります。例えば、「ワインのおいしさを判定するために以下の因子が存在する」と想定します。
- 熟成年数
- 甘さ(苦くない)
- 香り
- 色(見た目)
- 値段
これらについて、ワインごとの特徴が以下の通りだとします。
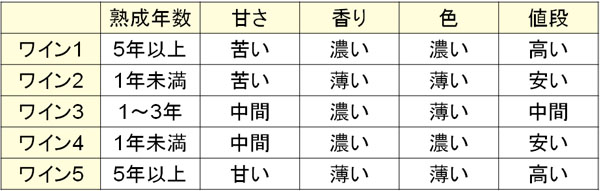
そこで強い相関があるケースと(普通の)相関があるケースを確認しましょう。例えば「ワイン1とワイン5」では、強い正の相関があります。そこでワイン1とワイン5に共通している部分を見つけると、以下のようになります。
- 熟成年数(5年以上)、値段(高い)
正の相関の場合、共通している部分を探しましょう。
一方で負の相関では、反対の結果となっている部分に着目しましょう。例えばワイン1とワイン2では、負の相関になっています。そこで反対の結果となっている部分を探すと以下のようになります。
- 熟成年数(1年未満・5年以上)、香り(濃い・薄い)、色(濃い、薄い)、値段(高い・安い)
そこで強い相関がある場合は2、普通の相関がある場合は1をつけましょう。以下のようになります。
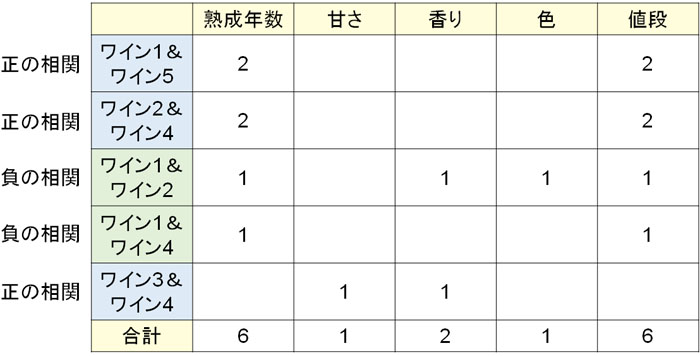
このように確認すると、今回の結果では熟成年数と値段が審査結果に大きな影響を与えることがわかります。つまりワインのおいしさで重要だったのは、熟成した高級品なのか安物だったのかの違いと推測できます。
要因について、相関の強さを調べることによって「何が結果に影響しているのか」を推測できるようになります。因子の数や内容は人が決定することになるため、バイアスは大きいものの、データの特性を要約するときには因子分析が便利です。
なお、より詳しい因子分析をする場合は統計ソフトを利用して以下の式を作ることになります。
- ワインのおいしさ=熟成年数\(×x_1+\)値段\(×x_2\)\(+e\)(独自因子)
なお当然ながら、ワインのおいしさが熟成年数と値段だけで決まることはありません。実際には他の要因も大きく関与します。ただ今回のように共通因子を設定する場合、熟成年数と値段がワインのおいしさの決定要因として重要というわけです。
多くの要素が含まれているとき、どのような因子が関係しているのか確認する手法を多変量解析といいます。多変量解析で最も重要なのは重相関分析であるものの、因子分析も多変量解析で利用されるというわけです。
因子分析をすることで関係している要素を見つける
統計学の手法の一つが因子分析です。データに隠れている共通因子を発見したいとき、因子分析を行うことになります。
さまざまな因子の影響によって結果が変わります。そこで相関係数を確認したり、共通因子は何かを推測したりして因子分析を進めましょう。
なお因子分析では人の考えが必ず入ります。そのためバイアスは大きく、因子分析によって発見した共通因子が必ず存在するとはいえません。探索的因子分析というのは、あくまでもデータを補完する要素にすぎません。
どのような因子によって結果を生じているのか把握できるのが因子分析のメリットです。ただバイアスが大きく、信頼性が低いというデメリットもあります。これらの事実を理解して因子分析を行うようにしましょう。






