熱力学で学ぶ内容として、気体による仕事があります。熱を加えることによって気体は膨張します。体積が増えると、その分だけ気体は物体を押します。つまり、気体が仕事をすることによって物体が動くのです。
力学では力のつり合いを学びます。気体が存在する場合、大気圧との力のつり合いを考えなければいけません。そこで、力のつり合いの式を作れるようになりましょう。また体積変化を計算することにより、気体による仕事量を得ることができます。
このとき利用されるグラフに\(P-V\)グラフがあります。圧力と体積の変化をグラフ化することにより、気体によって行われた仕事を確認できるのです。
それでは、どのように気体によって行われた仕事を計算すればいいのでしょうか。気体による圧力と力のつり合いや気体による仕事、仕事と\(P-V\)グラフの関係について解説していきます。
もくじ
圧力の定義と大気圧
静止している物体では、必ず力がつり合っています。このとき、気体が存在すると圧力が発生します。例えば大気圧というのは、酸素分子や窒素分子が衝突することによって起こっています。
分子による影響は非常に小さいです。ただ多くの分子が気体として存在することにより、圧力を生じるようになるのです。このとき、1m2当たりに生じる力を圧力といいます。
力が存在しなければ、当然ながら圧力は生まれません。そこで圧力\(P\)は力\(F\)と面積\(S\)を利用し、以下のように表されます。
- \(P=\displaystyle\frac{F}{S}\)
力を面積で割れば圧力になるのは当然なので、この公式を覚える必要はありません。
気体の圧力と力のつり合い
なお気体による圧力では、最も有名な圧力が大気圧です。約1013hPaが大気圧であり、大気圧は1気圧と定義されています。物体が空気に触れている場合、必ず大気圧による影響を受けています。
ほとんどの場合、物質は空気と接しています。そのため、大気圧と力がつり合っています。例えば、断面積\(S\)の容器内に質量\(m\)のピストンがあり、静止している場面を考えましょう。
下図の向きで容器が存在する場合、ピストンと容器との摩擦がないと仮定すると、容器内の圧力\(P_0\)と大気圧\(P_1\)には以下の関係があります。
\(P_0S=P_1S\)
\(P_0=P_1\)
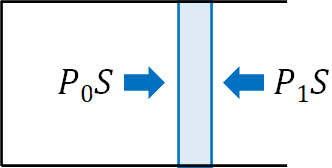
つまり、容器内の圧力と大気圧は同じです。なお公式を利用して計算しなくても、容器内の圧力と大気圧が同じであることはすべての人が理解できると思います。断面積が同じであるため、圧力が等しいのは当然です。
一方、下図の向きであれば先ほどとは異なり、ピストンの質量\(m\)を考慮しなければいけません。
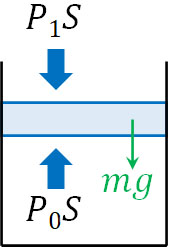
容器の内側では、容器内に存在する気体が上向きに\(P_0S\)の力で押しています。それに対して、上から下向きに大気圧\(P_1S\)による力とピストンによる重力\(mg\)が加わっています。そのため、力のつり合いは以下のようになっています。
\(P_0S=P_1S+mg\)
またこの式より、容器内の圧力\(P_0\)は以下のように計算できます。
\(P_0=P_1+\displaystyle\frac{mg}{S}\)
このように、力のつり合いの式を作ることで圧力の計算が可能です。
気体の体積の増減と仕事
次に、気体による仕事を学びましょう。「力\(F\)と移動距離\(x\)をかけることによって仕事\(W\)を得られる」と力学で習っていると思います。
- \(W=Fx\)
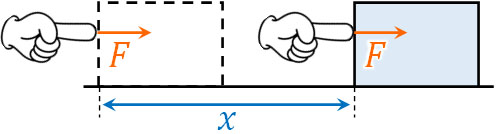
気体による仕事も同じように、力\(F\)と移動距離\(x\)を利用して計算します。例えば容器を熱すると、気体は膨張します。これによって気体がピストンを押す場合、気体による仕事は以下のように計算できます。
- \(W=PSx\)
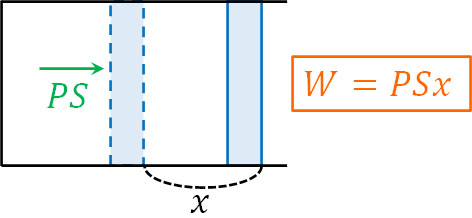
圧力に面積をかけると、力\(F\)を得ることができます。そのため仕事を得る公式を理解していれば、この公式を覚える必要はありません。また気体によって距離\(x\)が動くとき、表面積\(S\)は一定です。気体によって仕事が行われたとき、距離\(x\)の分だけ体積が増えます。
なお体積は表面積と高さ(移動距離\(x\))をかけることによって得られます。そのため、増えた体積\(ΔV\)を以下のように表すことができます。
- \(ΔV=xS\)
気体による仕事によって距離\(x\)を移動するというのは、体積が\(ΔV\)増えることを意味します。そこで、\(ΔV=xS\)を\(W=PSx\)に代入しましょう。そうすると、以下の公式を得られます。
- \(W=PΔV\)
圧力\(P\)が一定の場合、気体による仕事というのは、圧力と体積の変化量をかけることによって得られます。気体の体積が増えたら、気体は正の仕事をしたことになります。一方で気体の体積が減少したら、気体は負の仕事をした(気体は仕事をされた)ことになります。
\(P-V\)グラフの面積と気体による仕事の関係
気体による仕事を学ぶとき、\(P-V\)グラフがひんぱんに利用されます。たて軸を圧力\(P\)、横軸を体積\(V\)に設定して、圧力と体積の関係を表すのが\(P-V\)グラフです。
例えば圧力\(P\)が一定であり、気体の体積が\(V_1\)から\(V_2\)へ変化する場合、以下の図を作ることができます。

このとき重要なのは、気体がした仕事量はグラフの面積になるという事実です。前述の通り\(W=PΔV\)であり、グラフの面積と仕事量が一致しているとわかります。
なお圧力が一定でなかったとしても、グラフの面積は気体による仕事量となります。グラフが直線でも曲線でも、面積を確認すれば気体による仕事量を得られます。
なぜ\(P-V\)グラフを利用するのが重要なのでしょうか。先ほど記した公式\(W=PΔV\)は圧力が一定でなければいけません。つまり、圧力が一定でない場合はこの公式を利用することができません。
ただ実際には、圧力が一定ではないケースが多いです。その場合、公式を利用しても、気体による仕事量の計算ができません。そこでグラフを利用することで面積を計算し、気体によって行われた仕事を計算するのです。気体による仕事で\(P-V\)グラフを学ぶのはこうした理由があります。
符号の間違いに気を付けるべき
なお\(P-V\)グラフを利用して気体の仕事を計算するとき、符号がプラスなのか、それともマイナスなのか確認しましょう。同じグラフであっても、体積が増えているのか、それとも減っているのかによって符号が変わるからです。
例えば、以下の\(P-V\)グラフで気体がした仕事はいくらでしょうか。
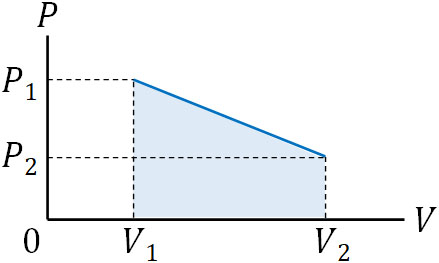
このグラフでは、仕事の計算はできません。理由としては、体積が増えたのか、それとも減ったのかわからないからです。体積が増えている場合、\(ΔV\)は正の値です。そのため仕事\(W\)は正の値になります。
一方で体積が減っている場合、\(ΔV\)は負の値です。そのため仕事\(W\)は負の値になります。そこで、体積の増減を確認しましょう。例えば、以下のケースはどうなるでしょうか。
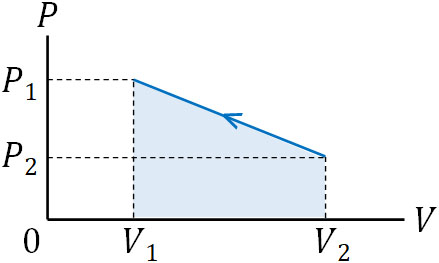
上図の場合、矢印の向きのように\(V_2\)から\(V_1\)へと体積が減っているので、気体によって負の仕事が行われているとわかります。そのため仕事(面積)を計算するとき、答えの符号は必ずマイナスになります。
\(P-V\)グラフでサイクルがある場合の計算
なお気体の圧力や体積を変化させた後、元の状態に戻るケースはよくあります。このときの仕事量について、\(P-V\)グラフを利用して問題を解きましょう。なお曲線があると積分をする必要があります。そこで理解しやすくするため、直線のグラフのみを考えます。
例えば、以下のグラフで気体がした仕事はいくらでしょうか。
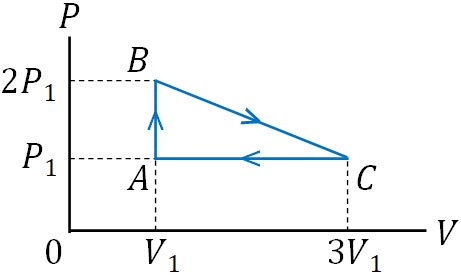
まず、AからBでは体積が増えても減ってもいません。つまり、気体による仕事量はゼロです。体積に変化がないため、気体は仕事をしていないのです。
一方、BからCでは体積が増えています。そのため、気体は正の仕事をしています。しかしCからAでは、体積が減っています。そのため、気体による仕事はマイナスになります。そこで、以下のように面積を計算しましょう。
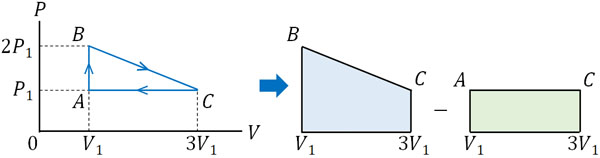
このように図を作ると、三角形ABCの面積を計算すれば、気体による仕事を計算できるとわかります。また、面積は正の値になります。そこで、以下のように式を作りましょう。
\(W=\displaystyle\frac{1}{2}×P_1×2V_1\)
\(W=P_1V_1\)
こうして、気体がした仕事\(W\)は\(P_1V_1\)と計算できます。サイクルの向きによっては答えがマイナスになることがあるため、前述の通り符号を必ず確認しましょう。
等温変化のグラフは反比例となる
なお\(P-V\)グラフで反比例の曲線が描かれていることがあります。以下の\(P-V\)グラフが該当します。
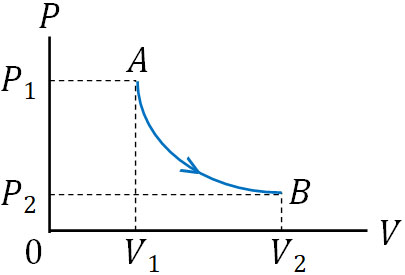
\(P-V\)グラフでAからBでは、どのような変化が起こっているのでしょうか。気体の状態方程式より、\(PV=nRT\)です。容器内に存在する気体の物質量\(n\)と定数\(R\)は一定であるため、温度が一定の場合、\(nRT\)は常に一定です。そのため、以下のようになります。
- \(PV=\)一定
そこで、\(nRT\)を定数\(a\)に変えましょう。そうすると、圧力\(P\)と体積\(V\)は反比例の関係になります。
\(PV=a\)
\(P=\displaystyle\frac{a}{V}\)
そのため\(P-V\)グラフで反比例の曲線が存在する場合、等温変化が起こっているとわかります。\(P-V\)グラフを確認することにより、こうした情報を得られるようになりましょう。
気体による仕事を学び、\(P-V\)グラフを理解する
力を加えることで物体が動く場合、仕事をすることになります。気体は体積が変化するため、気体によって行われた仕事を計算できるようになりましょう。
気体による仕事は\(PΔV\)で表されます。圧力が一定の場合、体積の変化量をかけることで仕事量を得られます。ただ、この公式は圧力が一定のときのみ利用できます。
そこで圧力が一定でなくても気体の仕事を計算できるようにするため、\(P-V\)グラフを利用しましょう。\(P-V\)グラフの面積を計算すると、気体による仕事量を得ることができます。注意点として、体積の増減を確認することで符号がプラスなのかマイナスなのか決定しましょう。
熱力学では気体による仕事を学びます。そこで気体の体積変化や\(P-V\)グラフの概念を理解し、気体による仕事量を計算しましょう。






