はね返り係数：物体衝突での公式や相対速度を利用する計算方法

物体が壁に衝突すると、物体は反対向きのスピードをもつようになります。言い換えると、物体は壁にはね返されることによって速度が変化します。

物体が壁に衝突後、どれだけの速度ではね返されるのかを表す指標に、はね返り係数（反発係数）があります。壁の性質によってはね返り係数は異なり、はね返り係数を利用することによって衝突後の物体の速度を計算できます。

またはね返り係数を利用することにより、動いている2つの物体が衝突した後の速度を計算できるようになりましょう。2つの物体の衝突では、相対速度を利用して計算します。

それでは、どのようにはね返り係数を利用して速度を計算すればいいのでしょうか。はね返り係数の概念や2つの物体による衝突後の速さ、運動量保存則との関係などを解説していきます。

1 速度を用いるはね返り係数（反発係数）の公式
- 1.1 ボールが壁に衝突する場合のはね返り係数
- 1.2 弾性衝突、非弾性衝突、完全非弾性衝突でのはね返り
2 2つの物体が衝突するときのはね返り係数と相対速度
- 2.1 はね返り係数（反発係数）を利用する練習問題
3 はね返り係数と運動量保存則を利用して式を作る

速度を用いるはね返り係数（反発係数）の公式

壁に衝突すると、すべての物体ははね返ります。壁が硬い場合、跳ね返った後であってもスピード減少はわずかです。一方で壁が柔らかい材質で作られている場合、はね返った後のスピードは遅いです。場合によっては衝撃がすべて壁に吸収され、はね返らずに物体が静止することもあります。

いずれにしても、物体が壁に衝突するとはね返ることになります。どれだけの速度ではね返されるのかを表すのがはね返り係数\(e\)です。はね返り係数\(e\)は以下の公式によって表されます。

\(e=-\displaystyle\frac{v_A’-v_B’}{v_A-v_B}\)

ただ、この公式は絶対に覚えないようにしましょう。物理では覚えてはいけない公式が非常に多く、その一つがはね返り係数です。公式を覚えるのではなく、なぜこの公式が導き出されるのか理解しましょう。

ボールが壁に衝突する場合のはね返り係数

はね返り係数とは、衝突後の速度の割合を表します。例えば10m/sの速度で動いているボールが壁に衝突した後、-3m/sの速度（反対向きに3m/sの速度）で動く場合、はね返り係数は0.3です。

はね返り係数がわかっている場合、衝突後の速度を簡単に計算できます。速度\(v\)で動いている物体について、壁に衝突後の速度\(v’\)は\(-ev\)と表すことができます。

なお壁に衝突後は反対向きの速度になるため、衝突後の速度は常に負の値になります。そのためはね返り係数を利用してかけ算をするとき、マイナスを加えます。

衝突後の速度がプラスというのは、はね返らずに壁を貫通していることを意味します。銃弾を利用するなど、特殊なケースを除き、衝突後の速度は負の値でなければいけません。

いずれにしても、はね返り係数を利用して衝突後の速度を計算できることを理解すれば、はね返り係数の公式を覚える意味はないとわかります。

弾性衝突、非弾性衝突、完全非弾性衝突でのはね返り

このときはね返り係数の値によって、物体のはね返りは以下の3種類に分けられます。

弾性衝突：\(e=1\)
非弾性衝突：\(0<e<1\)
完全非弾性衝突：\(e=0\)

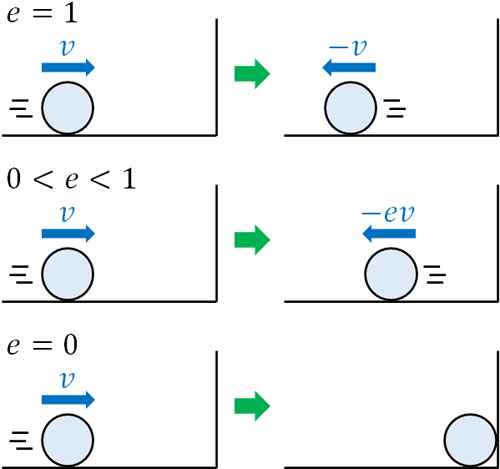
弾性衝突では\(e=1\)であるため、衝突前後の速度は同じです。それに対して、非弾性衝突では衝突後のスピードが落ちます。世の中の物理現象では、ほとんどが非弾性衝突です。また完全非弾性衝突では、物体が壁に衝突するとはね返らずに止まります。

なお通常、物体が衝突するときは力学的エネルギー保存則を利用できません。衝突によってエネルギーは熱や音に変わります。言い換えると、物体の衝突時は非弾性衝突となります。そのため物体が衝突するときは力学的エネルギー保存則ではなく、運動量保存則を利用して計算します。

しかし弾性衝突の場合、衝突前後のスピードが同じです。つまり、熱や音としてエネルギーの放出がありません。そのため弾性衝突の場合、例外的に力学的エネルギー保存則を利用できます。

2つの物体が衝突するときのはね返り係数と相対速度

次に、2つの動いている物体が衝突するときのはね返り係数（反発係数）を計算しましょう。動いている物体が衝突するという状況は、2つの物体の速度がそれぞれ異なることを意味します。そこで、相対速度を利用しましょう。

相対速度を利用するというのは、言い換えると「どちらか一方の物体を静止の状態と考えた場合、もう一方の物体はどれだけの速度で衝突するのか」を意味します。

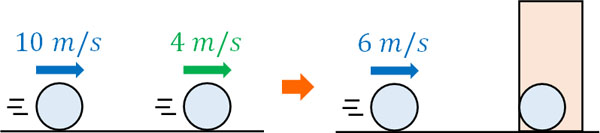
例えば10m/sで動いているボールAと4m/sで同方向に動いているボールBがあるとします。ボールBを静止の状態と考える場合、ボールBから見ると、ボールAは6m/sのスピードでボールBに向かって動いているとわかります。

一方でボールAを静止の状態と考える場合、ボールBは6m/sのスピードでボールAに向かって動いていることになります。

相対速度では、どちらを基準にしても問題ありません。相対速度を用いて計算するため、着目する物体を変えても当然ながら相対速度は一致します。

相対速度を利用すれば、一方の物体を静止させることができます。この場合、壁に衝突する場面と同じ状態を作れます。

そこで物体Aと物体Bについて、衝突前の速度を\(v_A,v_B\)、衝突後の速度を\(v_A’,v_B’\)としましょう。この場合、相対速度とはね返り係数を用いて以下の式を作ることができます。

\(v_A’-v_B’=-e(v_A-v_B)\)

また先ほどの式を変形すると、はね返り係数の公式を得られます。

\(e=-\displaystyle\frac{v_A’-v_B’}{v_A-v_B}\)

なお相対速度を利用するため、先ほどの計算式について、\(v_A\)と\(v_B\)が逆になっても問題ないです。つまり、以下の式を作ることができます。

\(v_B’-v_A’=-e(v_B-v_A)\)

どちらの物体を基準にしても結果は同じであり、公式を覚えても意味がありません。そうではなく、公式がもつ本質を理解しましょう。

なお物体の運動ではベクトルが重要になります。はね返り係数を利用できるのは、一直線上での運動です。そのため、必ずベクトルの向き（物体の運動の向き）に着目しましょう。

はね返り係数（反発係数）を利用する練習問題

それでは、はね返り係数（反発係数）を用いた物理の問題を解いてみましょう。以下の問題の答えは何でしょうか。

質量\(m\)の物体Aは右向きに速度\(2v\)で動いており、質量\(4m\)の物体Bは左向きに速度\(v\)で動いています。物体Aと物体Bは衝突し、衝突後の速度はそれぞれ\(v_A,v_B\)です。なお、はね返り係数は0.5です。

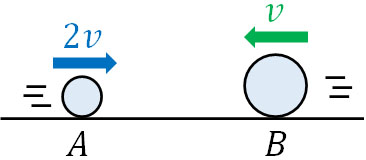
衝突後の物体Aと物体Bの速さを求めましょう。
物体Aが受けた力積を求めましょう。

1) 衝突後の物体Aと物体Bの速さを求めましょう

まず、運動量保存則を利用して式を作りましょう。以下のようになります。

\(m·2v+4m(-v)=mv_A+4mv_B\)

\(-2v=v_A+4v_B\)

次に、はね返り係数を利用して式を作りましょう。

\(v_A-v_B=-0.5(2v+v)\)

\(v_A-v_B=-1.5v\)

\(v_A=-\displaystyle\frac{3}{2}v+v_B\)

はね返り係数を利用して式を作るとき、式にマイナスを加えるのを忘れないようにしましょう。次に、\(v_A=-\displaystyle\frac{3}{2}v+v_B\)を\(-2v=v_A+4v_B\)に代入します。

\(-2v=v_A+4v_B\)

\(-2v=-\displaystyle\frac{3}{2}v+v_B+4v_B\)

\(-\displaystyle\frac{1}{2}v=5v_B\)

\(v_B=-\displaystyle\frac{1}{10}v\)

また\(v_A=-\displaystyle\frac{3}{2}v+v_B\)より、以下のように計算できます。

\(v_A=-\displaystyle\frac{3}{2}v+v_B\)

\(v_A=-\displaystyle\frac{3}{2}v-\displaystyle\frac{1}{10}v\)

\(v_A=-\displaystyle\frac{16}{10}v\)

\(v_A=-\displaystyle\frac{8}{5}v\)

こうして\(v_A=-\displaystyle\frac{8}{5}v\)、\(v_B=-\displaystyle\frac{1}{10}v\)と計算できました。言い換えると、衝突後に物体Aは左向きに\(\displaystyle\frac{8}{5}v\)、物体Bは左向きに\(\displaystyle\frac{1}{10}v\)のスピードで動きます。

2) 物体Aが受けた力積を求めましょう

運動量の変化を利用することで力積\(Ft\)を計算できます。運動量の変化後と変化前を利用し、以下の式を作りましょう。

\(Ft=m·-\displaystyle\frac{8}{5}v-2mv\)

\(Ft=-\displaystyle\frac{18}{5}mv\)

こうして、物体Aが受けた力積は\(-\displaystyle\frac{18}{5}mv\)と計算できました。