電気回路を学ぶとき、重要な法則にキルヒホッフの法則があります。キルヒホッフの法則には二種類あります。
キルヒホッフの法則は難しくありません。既に学んでいる内容を法則にしているにすぎません。既に学んでいる内容を法則化しただけであるため、キルヒホッフの法則で新たな内容は存在せず、復習となります。
ただキルヒホッフの法則を利用して計算することは多く、どのような法則なのか理解しておく必要があります。
それでは、キルヒホッフの法則の内容には具体的に何があるのでしょうか。電圧、電流、抵抗の関係について、キルヒホッフの法則を利用して解説していきます。
もくじ
電気回路のルールを表すキルヒホッフの法則
電気回路にはルールがあります。このルールを表すのがキルヒホッフの法則です。なお物理で電気を学んでいる場合、以下のルールがあることを既に知っていると思います。
- 回路を流れる電流の量は常に同じ(電流は消えたり増えたりしない)
- 電気回路を一周すると、電位差(電圧)は0になる
これらの内容の言い換えがキルヒホッフの法則です。キルヒホッフの法則には第一法則と第二法則があります。そこで、それぞれの内容を確認しましょう。
キルヒホッフの第一法則:電流の和は常に同じ
電気回路では、回路全体を流れる電流の量は常に同じです。そこでキルヒホッフの第一法則では、以下のように言い換えています。
- 回路内の分岐点や合流点について、電流の和は同じ
例えば電流\(I\)について、分岐点で\(I_1\)と\(I_2\)に分かれるとします。この場合、以下の式を作ることができます。
- \(I=I_1+I_2\)

それでは、回路内の合流点ではどのようになるのでしょうか。合流点で\(I_1\)と\(I_2\)が加わる場合、以下の式を作ることができます。
- \(I_1+I_2=I\)
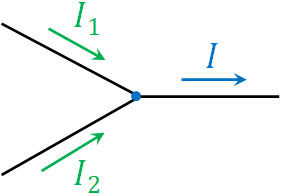
これがキルヒホッフの第一法則です。キルヒホッフの第一法則は容易に理解できると思います。
キルヒホッフの第二法則:回路を一周すると電位差が0になる
キルヒホッフの第二法則についても、内容は難しくありません。回路を一周すると電位差(電圧)はゼロになります。キルヒホッフの第二法則では、以下のように言い換えています。
- 任意の閉回路について、回路を一周すると電圧はゼロになる
閉回路とは、スイッチが閉じており、一周できる回路を指します。要は、回路を一周すると電位差がゼロになることを述べています。キルヒホッフの第二法則では電位差を考えるため、下図では以下の式が成り立ちます。
- \(V+(-RI)=0\)
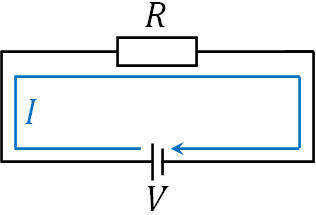
このように、電源による起電力と抵抗による電圧降下を足すとゼロになります。なお、電源は電位を上げるので符号はプラスであり、抵抗は電位を下げるので符号はマイナスです。
なおキルヒホッフの第二法則では、スタート地点はどこでもいいです。また回路を一周できる場合、どの経路を利用しても問題ありません。例えば下図のケースで考えてみましょう。
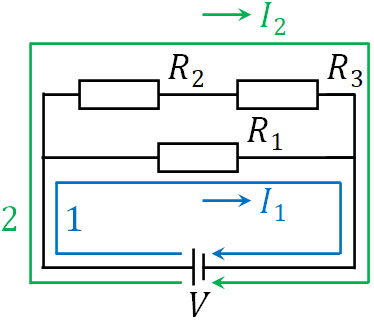
この場合、以下の2つの式を作ることができます。
- ルート1:\(V+(-R_1I_1)=0\)
- ルート2:\(V+(-R_2I_2)+(-R_3I_2)=0\)
一周すれば電位差が0になるため、キルヒホッフの第二法則を利用して式を作りましょう。
電源につながっていなくても第二法則を利用できる
なおキルヒホッフの第二法則で重要なのは、電源につながっていない場合であっても利用できることです。そこで先ほどの図について、以下のように回路を考えて式を作りましょう。
- \(-R_1I_1+(R_2I_2+R_3I_2)=0\)
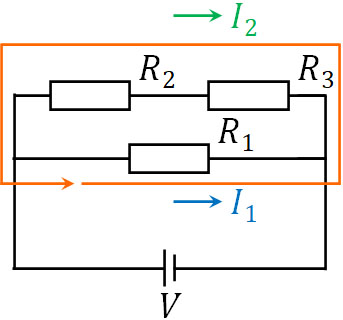
抵抗を通ると電位差が低くなるため、符号はマイナスになります。ただ\(R_2I_2+R_3I_2\)については、電流の向きに対して逆であるため、符号をプラスにしましょう。
なお、なぜこの式が成り立つかというと、電位差が同じだからです。並列接続の場合、電流の値は異なるものの、電位差(電圧)は等しいです。また、先ほどの式は以下のように変形できます。
- \(R_1I_1=R_2I_2+R_3I_2\)
並列接続では、電位差が同じになることは既に知っていると思います。電気の流れは水と同じであり、上から下に流れるときの高さ(電圧)というのは、途中で枝分かれしても値に変化がありません。
電源につながっていないルートであってもキルヒホッフの第二法則を利用できるというのは、新たな内容を学んでいるわけではなく、既にあなたが知っている内容を公式にしているにすぎません。
キルヒホッフの法則に関する練習問題
それでは、練習問題を解いてみましょう。実際にキルヒホッフの法則を利用することにより、どのように問題を解けばいいのか理解できます。以下の答えは何でしょうか。
- 以下の回路について、それぞれの抵抗に流れる電流の大きさと向きを求めましょう。
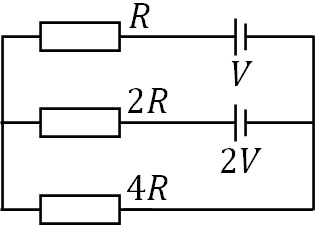
正電荷から負電荷へ電流が流れます。そこで、以下の図を作りましょう。
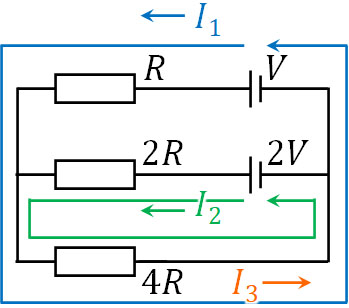
キルヒホッフの第一法則より、以下の関係が成り立ちます。
- \(I_1+I_2=I_3\)
また、キルヒホッフの第二法則を利用して式を作りましょう。2つのルートを利用すると、以下の式を作れます。
- \(V+(-RI_1)+(-4RI_3)=0\)
- \(2V+(-2RI_2)+(-4RI_3)=0\)
そこで、それぞれの式に\(I_1+I_2=I_3\)を代入しましょう。
・\(V+(-RI_1)+(-4RI_3)=0\)の計算
\(V+(-RI_1)+(-4RI_3)=0\)
\(V-RI_1-4R(I_1+I_2)=0\)
\(V-5RI_1-4RI_2=0\) – ①
・\(2V+(-2RI_2)+(-4RI_3)=0\)の計算
\(2V+(-2RI_2)+(-4RI_3)=0\)
\(2V-2RI_2-4R(I_1+I_2)=0\)
\(2V-4RI_1-6RI_2=0\)
\(V-2RI_1-3RI_2=0\) – ②
・\(I_2\)を計算する
連立方程式を解きましょう。\(①×2-②×5\)より、
\(-3V+7RI_2=0\)
\(7RI_2=3V\)
\(I_2=\displaystyle\frac{3V}{7R}\)
\(I_2=\displaystyle\frac{3V}{7R}\)であり、図の左向きに電流が流れているとわかります。
・\(I_1\)を計算する
次に、\(V-5RI_1-4RI_2=0\)を利用して\(I_1\)を計算しましょう。
\(V-5RI_1-4RI_2=0\)
\(V-5RI_1-4R×\displaystyle\frac{3V}{7R}=0\)
\(V-5RI_1-\displaystyle\frac{12V}{7}=0\)
\(5RI_1=-\displaystyle\frac{5V}{7}\)
\(I_1=-\displaystyle\frac{V}{7R}\)
こうして、\(I_1=-\displaystyle\frac{V}{7R}\)を得ることができました。なお答えが\(I_1=-\displaystyle\frac{V}{7R}\)であるため、電流は図の右向きとなります。
・\(I_3\)を計算する
また、\(I_1+I_2=I_3\)を利用すると\(I_3\)を計算できます。
\(I_1+I_2=I_3\)
\(I_3=-\displaystyle\frac{V}{7R}+\displaystyle\frac{3V}{7R}\)
\(I_3=\displaystyle\frac{2V}{7R}\)
計算結果より、\(I_3=\displaystyle\frac{2V}{7R}\)で図の右向きに電流が流れるとわかります。
電圧、電流、抵抗の関係を表すのがキルヒホッフの法則
キルヒホッフの法則は難しくなく、電気で既に学んでいる内容を法則として言い直しているのがキルヒホッフの法則です。
キルヒホッフの第一法則では、電流の和は常に同じです。またキルヒホッフの第二法則では、回路を一周すると電位差(電圧)の合計はゼロになります。
なお電源につながっていない経路であっても、キルヒホッフの第二法則が成り立ちます。並列接続では電位差が同じになるため、回路を一周すると電位差はゼロになるのです。第一法則と第二法則を利用し、連立方程式を解くことにより、電圧や電流、抵抗の計算が可能です。
内容は難しくないものの、電気回路の計算でひんぱんに利用される法則の一つがキルヒホッフの法則です。第一法則と第二法則を利用し、問題を解けるようになりましょう。






