磁場が変化すると、コイルに電流が流れます。磁石を近づけたり、遠ざけたりすることによって電気を得ることができるのです。
このとき、磁場が存在するのであれば、導体棒(金属棒)を利用することによって電磁誘導を起こし、電気を得ることができます。
それでは、なぜ導体棒が動くことによってコイルに電流が流れるのでしょうか。また、導体棒に生じる誘導起電力をどのように計算すればいいのでしょうか。このとき生じる誘導起電力はローレンツ力を用いて計算することもできます。
公式を覚えても計算できないため、必ず原理を理解しましょう。そこで、導体棒によって生じる誘導起電力に加えて、ローレンツ力を用いて電磁誘導が起こる原理を解説していきます。
もくじ
導体棒が動くことで面積が変化する
回路で電磁誘導がどのように利用されるのか確認しましょう。回路には導線があります。そこで、導線でつながれている以下の回路について考えてみましょう。
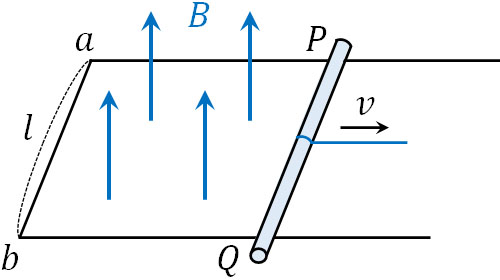
この回路は導線でつながれており、磁場(磁束密度\(B\))が存在します。このとき、回路を「1巻きのコイル」とみなすことができます。つまり導体棒が存在する場合、回路がコイルになるのです。
なお一様の磁場(磁束密度)が存在する場合、磁束密度は変化しません。しかし導体棒を速さ\(v\)で動かす場合、コイルの面積が多くなります。言い換えると、コイル内を貫く磁束が多くなります。
導体棒を速さ\(v\)で動かし、\(Δt\)秒の時間が経過する場合、動く距離は\(vΔt\)[m]です。そのため下図の場合、導体棒を動かすことによって増える面積\(ΔS\)は\(ΔS=lvΔt\)であり、この分だけコイルを貫く磁束が増えます。
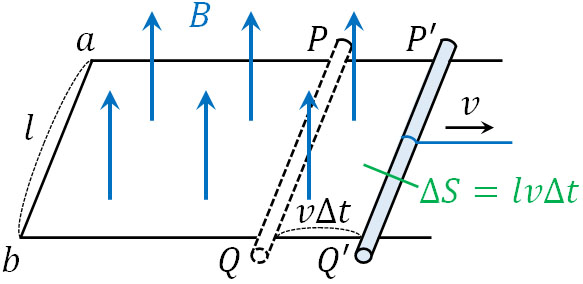
なぜ導体棒を動かすことによって電磁誘導を生じるかというと、コイルを貫く磁束が増えるからなのです。
磁束が増えると、コイルには磁束を減らすように電流が流れる
コイルは磁場の変化を嫌います。導体棒を動かすことによって磁束が増える場合、磁束を減らすようにコイルは磁場を作ります。そのため磁場(磁束密度)が下から上に向いているのであれば、コイルの磁場を減らすため、上から下の向きに新たな磁場(磁束密度)を発生させます。
そのため、電磁誘導によってコイルが作る新たな磁場(磁束密度)は以下のようになります。
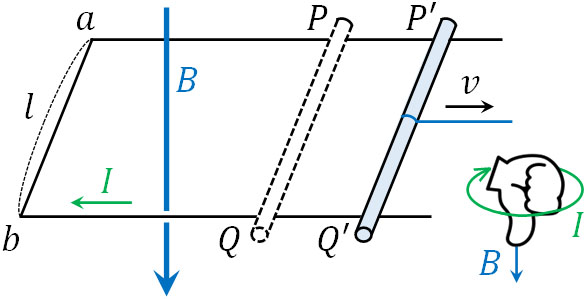
また右ねじの法則を利用すると、電流の向きがわかります。いずれにしても、このような原理によって電磁誘導が起こります。
・誘導起電力を計算する
前述の通り、導体棒を動かすことによって増える面積\(ΔS\)は\(ΔS=lvΔt\)です。また磁束密度は\(B\)なので、磁束変化\(ΔΦ\)は\(ΔΦ=BlvΔt\)です。コイルの巻数は\(N=1\)、経過時間は\(Δt\)であるため、ファラデーの電磁誘導の法則を利用すると、以下のように誘導起電力\(V\)を計算できます。
\(V=N\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)
\(V=1·\left|\displaystyle\frac{BlvΔt}{Δt}\right|\)
\(V=Blv\)
こうして、誘導起電力は\(V=Blv\)とわかりました。磁束密度\(B\)と長さ\(l\)が一定の場合、誘導起電力\(V\)は導体棒の速さ\(v\)に依存するとわかります。なお、公式として\(V=Blv\)を覚えるのではなく、式を作れるようになりましょう。
導体棒を動かすことによるジュール熱の発生と仕事
それでは、練習問題を解くことによって導体棒を動かすときのジュール熱と仕事を計算できるようになりましょう。以下の問題の答えは何でしょうか。
- 以下のように導線と抵抗\(R\)が置かれており、導線の上に導体棒があります。鉛直上向きの一様な磁場(磁束密度\(B\))が発生しているとき、導体棒を一定の速さ\(v\)で動かしました。なお、導体棒は導線に対して常に垂直であり、なめらかに動きます。
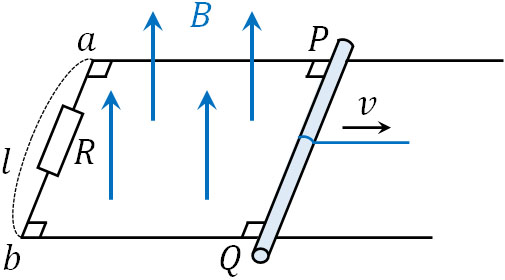
- \(t\)秒が経過するとき、抵抗で発生するジュール熱を求めましょう。
- 導体棒が磁場から受ける力の大きさ\(F\)と向きを求めましょう。
- あなたが導体棒を引いて\(t\)秒が経過するとき、仕事\(W\)はいくらですか。
1) \(t\)秒が経過するとき、抵抗で発生するジュール熱を求めましょう
先ほど解説した図とまったく同じなので、\(V=Blv\)です。そこで、\(V=Blv\)を利用して抵抗で発生するジュール熱を計算しましょう。
ジュールの法則より、以下の関係が成り立ちます。
- \(Q=IVt=I^2Rt=\displaystyle\frac{V^2t}{R}\)
この中で\(Q=\displaystyle\frac{V^2t}{R}\)を利用しましょう。つまり、以下のように計算します。
\(Q=\displaystyle\frac{V^2t}{R}\)
\(Q=\displaystyle\frac{(Blv)^2t}{R}\)
\(Q=\displaystyle\frac{B^2l^2v^2t}{R}\)
こうして、抵抗で発生するジュール熱は\(Q=\displaystyle\frac{B^2l^2v^2t}{R}\)とわかりました。
2) 導体棒が磁場から受ける力の大きさ\(F\)と向きを求めましょう
磁場が存在する場合、電流が流れることによって、磁場から電流に力が加わります。このとき、電流に加わる力\(F\)は以下の公式によって得ることができます。
- \(F=BIl\)
磁束密度\(B\)と導体棒の距離\(l\)は一定であり、既にわかっています。そこで、電磁誘導によって発生する電流\(I\)を計算しましょう。
抵抗\(R\)を流れる電流と導体棒を流れる電流は大きさが同じです。そこでオームの法則より、以下のように電流\(I\)を得ることができます。
\(V=RI\)
\(Blv=RI\)
\(I=\displaystyle\frac{Blv}{R}\)
そこで、\(I=\displaystyle\frac{Blv}{R}\)を\(F=BIl\)に代入しましょう。
\(F=BIl\)
\(F=Bl×\displaystyle\frac{Blv}{R}\)
\(F=\displaystyle\frac{B^2l^2v}{R}\)
こうして、\(F=\displaystyle\frac{B^2l^2v}{R}\)であるとわかりました。またフレミングの左手の法則より、図の左向きに力\(F\)が加わります。
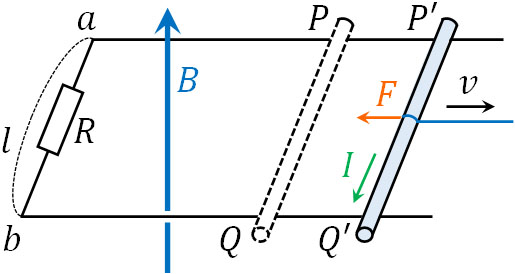
コイルは上から下向きに磁場を発生させます。ただ、外部磁場は下から上に発生しています。そこで外部磁場と電流の向きを考慮すると、力\(F\)は図の左向きになるのです。
3) あなたが導体棒を引いて\(t\)秒が経過するとき、仕事\(W\)はいくらですか
導体棒が動く速さは一定であるため、先ほど計算した力\(F\)とあなたが加える力はつり合っていると考えることができます。また、あなたが導体棒を引っ張る距離は\(vt\)です。そのため、以下のように計算できます。
\(W=Fx\)
\(W=\displaystyle\frac{B^2l^2v}{R}×vt\)
\(W=\displaystyle\frac{B^2l^2v^2t}{R}\)
こうして、仕事\(W\)は\(W=\displaystyle\frac{B^2l^2v^2t}{R}\)と計算できました。
ローレンツ力と電力棒に生じる誘導起電力
ここまで、レンツの法則とファラデーの電磁誘導の法則を利用することにより、導体棒に生じる誘導電流と誘導起電力を解説してきました。それでは、一つの電子に着目する場合はどのように計算すればいいのでしょうか。
導体棒に発生する誘導起電力はローレンツ力を用いることで説明することもできます。
レンツの法則により、導線と導体棒には誘導電流が流れます。このとき、導体棒に誘導起電力が発生します。つまり以下のように、導体棒に起電力が発生するため、導体棒は電源のように機能するのです。
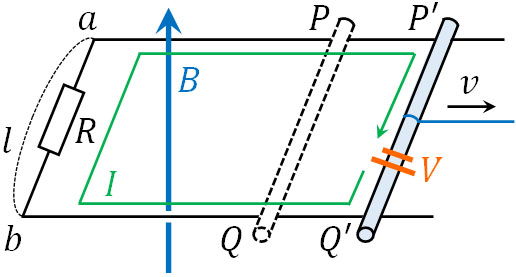
それでは、なぜ導体棒に誘導起電力が発生するのでしょうか。導体棒が動くことにより、回路のほかの場所に誘導起電力が発生する可能性はないのでしょうか。
自由電子の動きとローレンツ力を用いた誘導起電力の計算
そこで、導体内部の自由電子に着目しましょう。導体棒を右に動かすと、当然ながら導体に存在する自由電子も右に動くことになります。このとき磁場が存在する場合、電子が動くとローレンツ力が発生します。
なお、導体棒を動かすことによって電子が右に移動するというのは、左向きに電流が流れたことを意味します。そこでフレミングの左手の法則を利用し、ローレンツ力の向きを記すと下図のようになります。
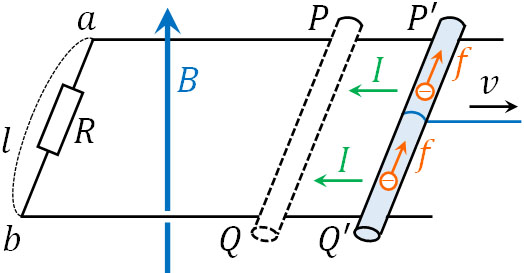
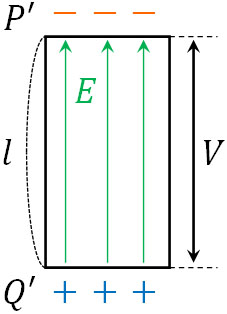
導体棒の中に存在する電子が移動するため、電荷の偏りを生じます。上図であれば、\(Q’\)は正電荷となり、\(P’\)は負電荷となります。電荷の偏りによって、導体棒では電圧(誘導起電力)\(V\)を生じるのです。
ローレンツ力と電場による力がつり合う
ローレンツ力が電子に働くことで電荷の偏りを生じると、新たに電場\(E\)を生じます。正電荷と負電荷がある場合、そこには電圧が存在し、正電荷から負電荷に向けて電場が発せられているのです。
このとき電子は負電荷であるため、正電荷へ引き寄せられます。つまり、ローレンツ力\(f\)によって電子は\(P’\)へ移動するものの、新たに発生した電場\(E\)の影響を受けて点\(Q’\)へ引き寄せられる力(静電気力)\(F\)が働くのです。
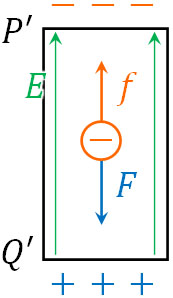
電場\(E\)が大きくなると、それに伴って静電気力\(F\)も大きくなります。こうして、どこかの時点でローレンツ力\(f\)と静電気力\(F\)がつり合います。
それでは、力がつり合っている状態での電場\(E\)と誘導起電力\(V\)を求めましょう。静電気力の大きさは\(F=qE\)で得ることができるため、電子の電気量を\(-e\)とすると、一つの電子に加わる静電気力は\(F=eE\)となります。
また、ローレンツ力の公式は\(f=qvB\)であるため、一つの電子に加わるローレンツ力は\(f=evB\)です。\(f=F\)であるため、以下のように計算しましょう。
\(f=F\)
\(evB=eE\)
\(E=vB\)
こうして、\(E=vB\)とわかりました。つまり、導体棒を動かすスピード\(v\)が速いほど、導体内に生じる電場が大きくなります。
電場を利用して誘導起電力の大きさを得る
それでは、ローレンツ力を利用して誘導起電力を計算しましょう。計算方法は簡単であり、導体棒の長さ\(l\)と電場\(E\)を利用することで誘導起電力\(V\)を計算します。
電場を学ぶとき、\(V=El\)を公式として必ず学びます。電場\(E\)は傾きであり、先ほどの公式を変形することで\(E=\displaystyle\frac{V}{l}\)と表すこともできます。
なお\(E=vB\)であるため、以下のように誘導起電力を計算しましょう。
\(E=\displaystyle\frac{V}{l}\)
\(vB=\displaystyle\frac{V}{l}\)
\(V=Blv\)
こうして、ファラデーの電磁誘導の法則を利用して誘導起電力を計算した方法と同じ答えを得ることができました。一つの電子に着目することによっても、誘導起電力の計算を行うことができるのです。
なお、もし導体棒以外の場所に誘導起電力\(V’\)が存在する場合、回路全体の誘導起電力は以下のようになります。
- \(V=Blv+V’\)
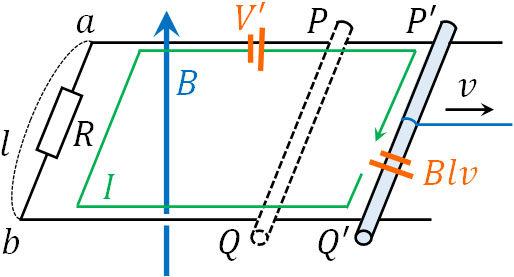
これではファラデーの電磁誘導の法則に矛盾するため、導体棒が動くときは導体棒が誘導起電力となるのです。つまり、導体棒以外の場所の誘導起電力\(V’\)はゼロである必要があります。
導体棒を動かすときに起こる現象を学ぶ
回路に導体棒が存在するケースがあります。この場合、回路の形によっては、導体棒と回路を一つのコイルとみなすことができます。
磁場が存在する場合、導体棒が磁束と垂直方向になるように動かすことで電磁誘導が起こります。新たに誘導電流が発生し、誘導起電力を得ることができるのです。そこで、レンツの法則とファラデーの電磁誘導の法則を利用して、誘導起電力の大きさと向きを求められるようになりましょう。
また、一つの電子に着目することで誘導起電力を計算することも可能です。ローレンツ力を利用し、電場との力のつり合いを利用することによって同じ公式を得ることができるのです。
これらの公式は覚えるのではなく、計算によって導出できるようになりましょう。物理では公式を暗記しても意味がないため、物理現象が起こる原理を学び、応用問題を含めて解けるようになりましょう。






