電場：一様な電場・点電場の公式、電場の重ね合わせとベクトル

何も触れていない場合、物体に力が加わることはありません。ただ例外的に、場が存在する場合は物体に触れていなくても力が加わります。重力が良い例であり、空中に存在している物体（何も触れていない物体）を含めて、すべての物体には重力が加わっています。

こうした場として、重力以外にも電場（電界）があります。電場がある場合、電荷をもつ物質に力が加えられることによって物質は動くのです。

電場には、一様な電場と点電荷による電場があります。それぞれの電場で利用する公式を覚えなければいけません。また複数の電場が存在するとき、どのように力が加わるのか計算できるようになる必要があります。

それでは、電場を利用して力の大きさや向きを知るにはどうすればいいのでしょうか。電磁気で重要な電場の概念や公式、力の計算方法を解説していきます。

1 電場の大きさと向きの定義
2 電場の重ね合わせとベクトル
- 2.1 2つの点電荷による電場の大きさに関する練習問題
3 電場の定義を学び、ベクトルを考慮して計算する

電場の大きさと向きの定義

まず、電場とは何かを理解しましょう。場がない場合、ほかの物体に触れていないのであれば、力は働きません。例えば宇宙空間では、重力という場が存在しないため私たちは宙に浮きます。

また場の強さ（大きさ）も重要です。月であれば、重力は地球の6分の1です。場が強いのか、それとも弱いのかによって物体に加わる力の大きさが異なるのです。

こうした場の一種が電場（電界）です。電荷をもつ物質であれば、電場が存在することによって、ほかの物質に触れていなくても力をもつようになります。つまり、電荷をもつ物質は電場の影響を受けて動きます。また、力の大きさは電場の強さに比例します。

多くの場合、電場は記号\(E\)を用います。また、電場の単位はN/Cです。電気的な大きさを利用して力の強さを表すため、力の大きさN（ニュートン）と電気量C（クーロン）を利用して電場を表すのです。

それでは、大きさ\(E\)[N/C]の電場が右向きで存在する場面を考えましょう。この電場に3Cの点電荷と-2Cの点電荷を置く場合、どのような大きさと向きで力が加わるでしょうか。以下のようになります。

3Cの点電荷：右向きに\(3E\)[N]の力が加わる。
-2Cの点電荷：左向きに\(2E\)[N]の力（右向きに\(-2E\)[N]の力）が加わる。

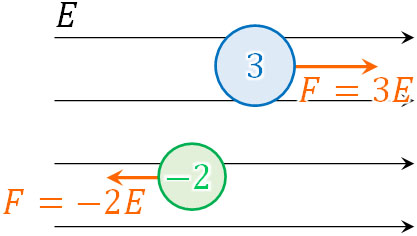
正の電荷をもつ物質では、電場と同じ向きに力が加わります。一方で負の電荷をもつ物質では、電場と反対向きに力が加わります。また、力の大きさ\(F\)は電場\(E\)と電気量\(q\)を利用して、以下のように表されます。

\(F=qE\)

この公式は非常に重要であるため、必ず覚えましょう。

点電荷が1Cの場合、\(F=qE\)に\(q=1\)を代入すると、\(F=E\)となります。つまり電場というのは、1Cの点電荷に対して与える力の大きさと向きを表します。これが電場の定義です。

一様な電場と力の大きさの公式

なお電場には大きく2種類あります。一つが一様な電場であり、もう一つが点電荷による電場です。まず、一様な電場を確認しましょう。

一様な電場では、どの場所であっても電場の大きさが同じになります。大きさが同じ金属板を平行に置き、一方を正に帯電させ、もう一方を負に帯電させます。そうすると、電場の向きはプラスからマイナスの方向になります。

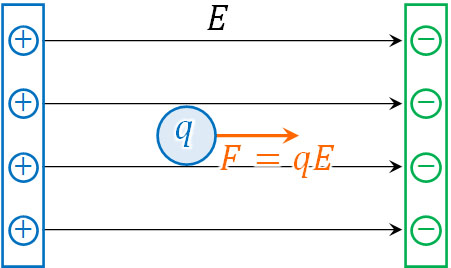
一様な電場では、点電荷を置くことによって力の大きさは\(F=qE\)となります。この公式は先ほど解説しました。

なお、先ほどの公式を変形して\(E=\displaystyle\frac{F}{q}\)にしましょう。これにより、力の大きさ\(F\)と電気量\(q\)を利用することで電場\(E\)を得られます。

点電荷による電場の概念

それでは棒状の金属板を利用して均一な電場を発生させるのではなく、2つの点電荷を利用することで電場を発生させる場合はどうなるのでしょうか。

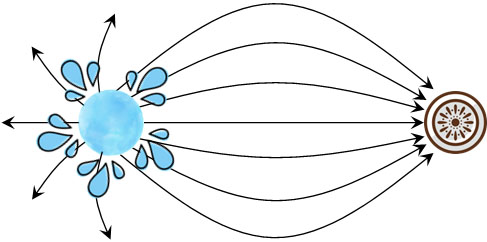
一つの点から温泉が湧き出ており、少し離れた場所に排水溝がある場面を考えてみましょう。一つの点から温泉が湧き出るとき、放射状に水が外に出ます。そのうち、排水溝に向かって飛び出た水については、排水溝へ吸い込まれます。具体的には、以下のような進み方になります。

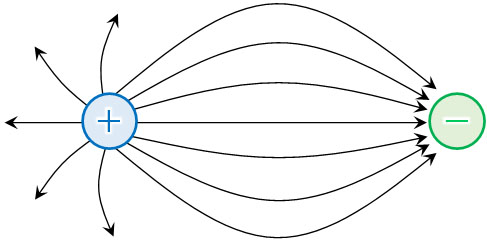
点電荷を利用する場合についても、これとまったく同じ進み方となります。正の電荷をもつ点電荷を置く場合、点電荷から放射状に電場が発せられます。

また、正の電荷をもつ点電荷から少し離れた場所に負の電荷をもつ点電荷を置きます。この場合、正の点電荷から発せられた電場は、負の点電荷へ進み、吸い込まれます。

電場（電界）は目で見えないので想像しにくいです。そこで水が一つの点から勢いよくあふれ出ている場面を想像しましょう。そうすれば、点電荷を利用することで発生する電場を理解しやすくなります。水の進み方も電場の進み方も同じなのです。

点電荷による電場の大きさと公式

一様な電場では、場所によって電場の強さに違いはありません。どの場所に点電荷を置いたとしても、電場の強さは一定です。

一方で点電荷による電場というのは、場所によって電場の強さが異なります。電場を作っている点電荷から離れると、当然ながら影響力は弱くなります。つまり、点電荷から離れるほど電場の大きさは弱くなります。

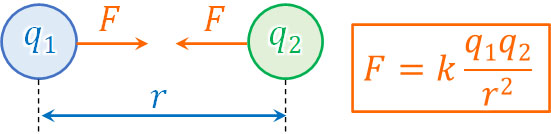
それでは、点電荷による電場の強さを計算するにはどうすればいいのでしょうか。クーロンの法則より、静電気力（クーロン力）の大きさ\(F\)は以下の公式によって得ることができます。

\(F=k\displaystyle\frac{q_1q_2}{r^2}\)

また電場の定義より、1Cの点電荷に対して加わる力を表すのが電場です。そこで点電荷による電場の大きさを計算するとき、電場を作っている点電荷の電気量を\(Q\)[C]、そこから\(r\)[m]離れた場所に1Cの点電荷を置く場面を考えましょう。

この場合、\(q_1=Q\)と\(q_2=1\)を代入することで以下の式を得ることができます。

\(F=k\displaystyle\frac{Q}{r^2}\)

1Cの電荷が受ける力\(F\)が\(k\displaystyle\frac{Q}{r^2}\)であるため、この式は電場\(E\)を表しています。つまり、点電荷による電場の大きさは以下の公式になります。

\(E=k\displaystyle\frac{Q}{r^2}\)

点電荷による電場の大きさを得る公式を覚える必要はありません。クーロンの法則を利用し、\(q_1=Q\)と\(q_2=1\)を代入すれば、公式を得ることができるからです。

なお、力の向きは点電荷によって異なります。例えば\(+Q\)[C]の点電荷によって電場が作られている場合、1Cの点電荷を置くと、同符号であるため、斥力（反発する力）が加わります。一方で\(-Q\)[C]の点電荷によって電場が作られている場合、1Cの点電荷を置くと、引力によって引き寄せられます。

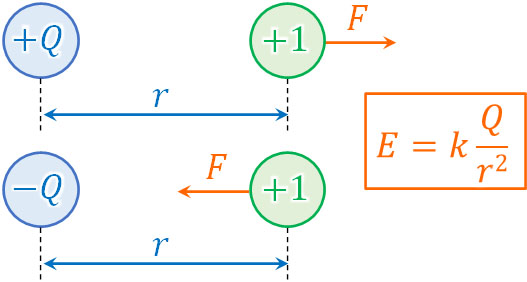
\(E=k\displaystyle\frac{Q}{r^2}\)によって電場の大きさがわかっても、力の向きはわかりません。そこで、点電荷が正なのか負なのかを確認することにより、働く力（斥力または引力）を確かめるようにしましょう。

\(F=qE\)は一様な電場でも点電荷による電場でも成立する

なお、一様な電場でも点電荷による電場でも\(F=qE\)が成立します。一様な電場では、どの場所に点電荷を置いても電場の大きさが同じです。一方で点電荷による電場では、場所によって電場の大きさが変化します。ただ\(F=qE\)によって、力の大きさを計算できるのは共通しているのです。

例えば点電荷による電場であれば、\(E=k\displaystyle\frac{Q}{r^2}\)を利用して電場の大きさを出しましょう。例えば点電荷による電場\(E\)が存在するとき、電気量\(q’\)の点電荷を置く場合、加わる力は以下のようになります。

\(F=qE\)

\(F=q’×k\displaystyle\frac{Q}{r^2}\)

\(F=k\displaystyle\frac{Qq’}{r^2}\)

こうして、クーロンの法則とまったく同じ公式を得ることができました。クーロンの法則を利用して電場の公式を出しているため、電気量\(q’\)をかけることで静電気力（クーロン力）の大きさを計算できるのです。

電場の大きさ\(E\)と電気力\(q\)のかけ算によって力\(F\)を得るというのは、静電気力の大きさを得るのと意味が同じです。

電場の重ね合わせとベクトル

一つの点電荷を置くことにより、電場が発生します。ただ電場の発生に関わる点電荷が一つではなく、複数存在するケースもあります。この場合、どのように考えて電場の大きさを計算すればいいのでしょうか。

物理ではベクトルをひんぱんに利用します。電場についても、それぞれの電場を足すことによって、電場の大きさを計算しましょう。なお電場には向きがあるため、ベクトルを考慮して足し算をする必要があります。

例えば点Aと点Bにそれぞれの電気量が\(Q_A\)と\(Q_B\)の点電荷を置きます。この場合、点Pに生じる電場は以下のようになります。

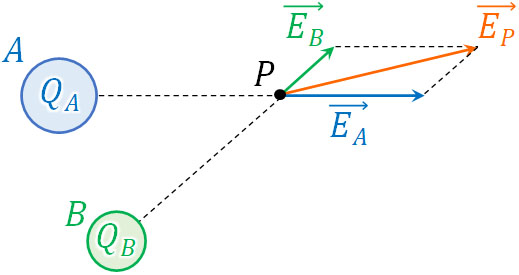
点Aによる電場\(\overrightarrow{E_A}\)と点Bによる電場\(\overrightarrow{E_B}\)を足すことにより、電場\(\overrightarrow{E_P}\)を得ることができます。ベクトルの足し算によって電場の大きさを得られることを電場の重ね合わせの原理といいます。

2つの点電荷による電場の大きさに関する練習問題

それでは、電場の重ね合わせの原理を利用することによって電場の大きさを計算しましょう。以下の問題の答えは何でしょうか。

\(xy\)平面上の点A\((-a,0)\)に電気量\(q\)、点B\((a,0)\)に電気量\(-q\)の点電荷が存在します。なお、クーロンの法則の比例定数を\(k\)とします。

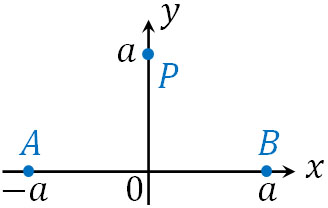
点P\((0,a)\)に作られる電場の大きさ\(E_P\)を求めましょう。
点B\((a,0)\)の電気量を\(4q\)に変える場合、電場が0になる点を求めましょう。

1) 点P\((0,a)\)に作られる電場の大きさ\(E_P\)を求めましょう

点Pに作られる電場は点Aと点Bによる影響を受けます。電気量\(q\)の点電荷が点Aにあるため、点Aによる電場の強さ\(E_A\)は以下のように計算できます。

\(E_A=k\displaystyle\frac{q}{(\sqrt{2}a)^2}=\displaystyle\frac{kq}{2a^2}\)

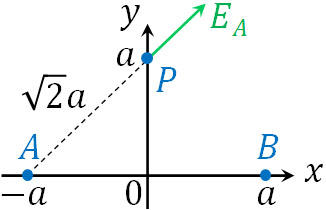
なお点Aは正電荷であるため、斥力によって反発します。一方、電気量\(-q\)の点電荷が点Bにあるとき、点Bによる電場の強さ\(E_B\)は以下のように計算できます。

\(E_B=k\displaystyle\frac{q}{(\sqrt{2}a)^2}=\displaystyle\frac{kq}{2a^2}\)

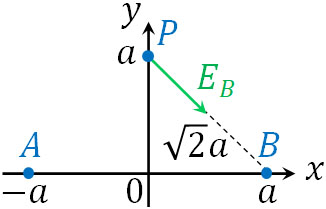
点Bは負電荷であるため、引力によって点Bへ引き寄せる力が働きます。そこで点Aと点Bによる電場を足すと、点Pでの電場の大きさを計算できます。

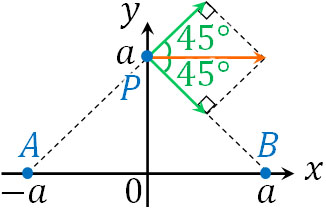
図より、点Pでの電場の大きさ\(E_P\)は以下のように計算できます。

\(E_P=\displaystyle\frac{\sqrt{2}kq}{2a^2}\)

値の大きさと向き（ベクトル）を考慮して、電場の重ね合わせの原理を利用しましょう。

2) 点B\((a,0)\)の電気量を\(4q\)に変える場合、電場が0になる点を求めましょう

点Aの点電荷は変わらず、点Bの点電荷が\(4q\)になる場合、以下の図を作ることができます。

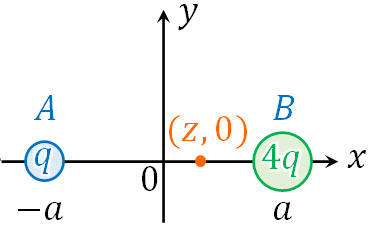
電場はベクトルの足し算になるため、電場が0になる点は必ず\(x\)軸上に存在します。\(x\)軸上でない場合、\(y\)軸方向に電場が必ず存在することになります。そこで電場が0となる\(x\)軸上の点を\((z,0)\)としましょう。

このとき、点Aによる電場と点Bによる電場が等しい場合、電場は0になります。そこで、以下の式を作りましょう。

\(E_A=E_B\)

\(k\displaystyle\frac{q}{(a+z)^2}=k\displaystyle\frac{4q}{(a-z)^2}\)

\((a-z)^2=4(a+z)^2\)

\(a^2-2az+z^2=4(a^2-2az+z^2)\)

\(3a^2-6az+3z^2=0\)

\((3a-z)(a-3z)=0\)

\(z=\displaystyle\frac{a}{3},3a\)

なお電場が0になるためには、\(z\)の値が\(-a<z<a\)でなければいけません（\(-a\)と\(a\)の間に\(z\)がある）。\(z=3a\)の場合、下図のように、ベクトル（向き）を考慮すると電場は0になりません。

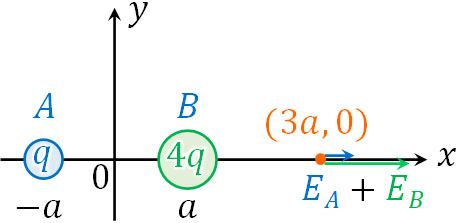
数学であれば、\(z=3a\)であっても答えが0になるので正解です。しかし、物理でベクトルを考慮する場合、\(z=3a\)は答えではありません。そのため\(z=\displaystyle\frac{a}{3}\)となり、\(\left(\displaystyle\frac{a}{3},0\right)\)が正解です。