導線に電流を流すことにより、磁場が発生します。コイルは磁場の変化を嫌うため、磁場の変化があると、コイルは自身に電流を流すことによって新たな磁場を作る性質があります。このときコイルに電流が流れると磁場が作られ、この新たな磁場の変化を抑えるためにさらに磁場を作ろうとします。
そのためコイルに電流が流れると、複数の磁場が作られるようになります。自分の影響によって電磁誘導が起こる現象を自己誘導と呼び、自己誘導で発生する誘導起電力を計算できるようになる必要があります。
また、コイルは他のコイルの影響によっても誘電起電力が発生します。これを相互誘導と呼び、相互誘導による誘電起電力を計算できるようにならなければいけません。
それでは、自己誘導と相互誘導の原理はどうなっているのでしょうか。また、どのように誘導起電力を計算すればいいのでしょうか。これらの現象が起こる理由と公式の導出方法を解説していきます。
もくじ
回路内のコイルは電流の変化で誘電起電力が発生する
電流が流れると、その周辺に磁場が生まれます。以下のように、電流\(I\)に対して垂直に磁場\(H\)が発生するのです。
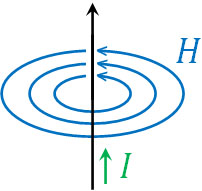
コイルは導線で構成されているため、コイルに電流が流れると、電磁誘導によって磁場を作ります。ただコイルは磁場の変化を嫌います。
そのためコイルに電流が流れることで磁場が発生すると、この磁場の影響を抑えるようにほかの磁場が発生します。つまり、コイル自身が作り出した磁場に対して電磁誘導が起こり、誘電起電力が発生します。この現象を自己誘導といいます。
例えば以下のように、電流\(I\)が流れている状態に対して、電流が\(ΔI\)増えるとします。電流は\(I\)から\(I+ΔI\)となるため、電流の値が大きくなった分だけ磁場が強くなります。
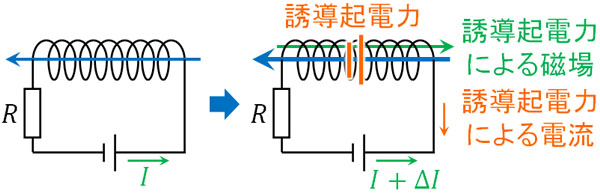
この場合、大きくなった磁場を弱める向きに新たな磁場が作られます。こうして電磁誘導が起こり、コイルで誘導起電力が生まれ、誘導電流が流れます。
それに対して、電流を\(ΔI\)だけ少なくなる場合はどうなるのでしょうか。この場合、コイル周辺の磁場が弱まります。そこで、コイルは磁場を強めるように磁場を発生させます。
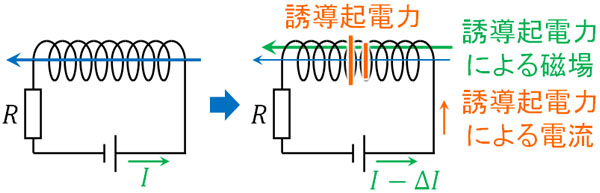
こうして、先ほどとは反対向きに誘導起電力と誘導電流が発生します。
自己誘導起電力の計算方法:自己インダクタンス
それでは、誘導起電力を計算できるようになりましょう。自己誘導による誘導起電力(自己誘導起電力)を得るためには、以下の公式を利用します。
- ファラデーの電磁誘導の法則:\(V=N\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)
- ソレノイドが作る磁場:\(H=nI\)
- 磁束密度の公式:\(B=μH\)
- 磁束の公式:\(Φ=BS\)
まず以下のように、変化する値に対して\(Δ\)を加えましょう。
- ソレノイドが作る磁場:\(ΔH=nΔI\)
- 磁束密度の公式:\(ΔB=μΔH\)
- 磁束の公式:\(ΔΦ=ΔBS\)
そうすると、以下のように計算できます。
\(ΔΦ=ΔBS\)
\(ΔΦ=μΔHS\)
\(ΔΦ=μnΔIS\)
そこで、\(ΔΦ=μnΔIS\)を\(V=N\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)に代入しましょう。
\(V=N\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)
\(V=N\left|\displaystyle\frac{μnΔIS}{Δt}\right|\)
\(V=NμnS\left|\displaystyle\frac{ΔI}{Δt}\right|\)
\(N\)はコイルの巻数であり、\(n\)は1mあたりのコイルの巻数なので区別しましょう。参考までに、コイルの長さが\(l\)[m]の場合、\(N=nl\)です。また、\(n=\displaystyle\frac{N}{l}\)と表すこともできます。
それでは、\(V=NμnS\left|\displaystyle\frac{ΔI}{Δt}\right|\)を得ることで考察できる内容は何でしょうか。コイルの違いによって巻数\(N\)、透磁率\(μ\)、単位長さ当たりの巻数\(n\)、コイルの断面積\(S\)は決まっています。そのため使用するコイルが決まれば、\(NμnS\)は定数です。
そこで、\(NμnS=L\)としましょう。この場合、先ほどの式は以下のようになります。
- \(V=L\left|\displaystyle\frac{ΔI}{Δt}\right|\)
\(L\)の値はコイルの違いによって変化し、自己インダクタンスと呼ばれます。自己インダクタンスが大きいコイルでは、自己誘導起電力も大きくなります。一方、自己インダクタンスが小さいコイルでは、自己誘導起電力も小さくなります。
自己誘導による誘導電流の向きを確認する
次に、自己誘導による誘導電流の向きを確認しましょう。電磁誘導によって電場が発生したのであれば、右ネジの法則によって電流の向きがわかります。ただ、より簡単に判断する方法があります。以下のように考えましょう。
- 電流が増えたとき(または減ったとき)、電流の変化をなくすように電流が流れる。
例えば電流が\(ΔI\)だけ増えたのであれば、その分だけ磁場が増えます。そこで、「\(ΔI\)とは反対向きに電流を流せば、増えた磁場を打ち消すことができる」とわかります。
同様に電流が\(ΔI\)だけ減ったのであれば、その分だけ磁場が減ります。そこで、\(ΔI\)と同じ方向に電流を流せば、減った磁場を補うことができます。
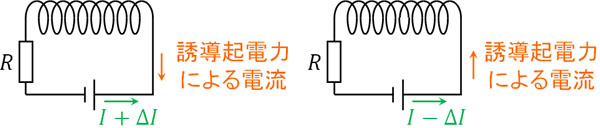
コイルを流れる電流が増えたのか、それとも減ったのかを確認しましょう。電流の変化に対して反対の現象を起こすのが自己誘導での誘導電流です。
2つのコイルによる電磁誘導が相互誘導
なお、コイルに流れる電流が変化するとき、ほかのコイルの影響を受けることもあります。このとき、ほかのコイルの影響によって電磁誘導を起こす現象を相互誘導といいます。
例えば以下のように、同じ鉄心に2つのコイルが存在するとします。
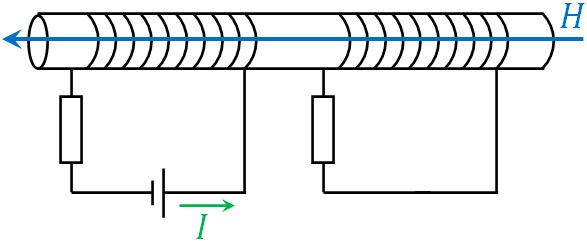
このとき電源に接続しており、電流が流れるコイルを一次コイルといいます。一方、電流のないコイルを二次コイルといいます。
一次コイルに流れる電流を\(ΔI\)増やす場合、磁場が大きくなります。そのため、一次コイルでは\(ΔI\)とは逆向きに誘導電流\(I’\)が流れ、磁場を弱めようとします。また二次コイルについても、一次コイルの影響によって同様に磁場が大きくなるため、一次コイルと同じ向きで電磁誘導が起こります。

それに対して、電流を\(ΔI\)ほど弱める場合、電場が弱まります。そこで、電場を強めるように一次コイルでは自己誘導が起こります。同時に、二次コイルでも相互誘導によって電場を強めるように電流が流れます。
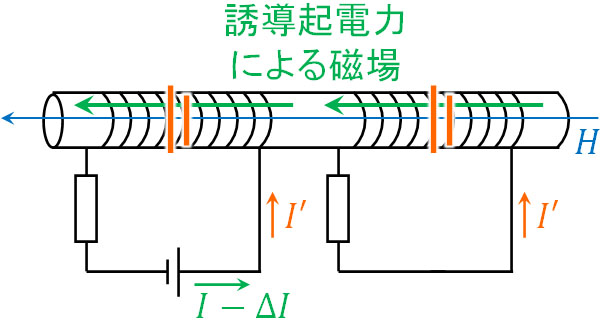
一次コイルと二次コイルでは、誘導起電力や誘導電流の向きは同じになります。
相互誘導起電力の計算方法
それでは、相互誘導による誘導起電力(相互誘導起電力)はどのように計算すればいいのでしょうか。
先ほど、\(V=L\left|\displaystyle\frac{ΔI}{Δt}\right|\)を利用して自己誘導起電力を計算できると解説しました。一次コイルでも二次コイルでも、起こるのは磁場の変化であり、向きは同じです。そのため二次コイルの誘導起電力を計算するとき、これと似た公式を利用すればいいとわかります。
ただ一次コイルと二次コイルでは、コイルの種類など条件が異なるケースがあります。当然、条件が異なると自己インダクタンス\(L\)を利用できません。そこで、二次コイルでは自己インダクタンス\(L\)の代わりに相互インダクタンス\(M\)を利用しましょう。
- \(V=M\left|\displaystyle\frac{ΔI}{Δt}\right|\)
自己インダクタンスと同じように、相互インダクタンスもコイルの種類によって決まります。両方とも、コイルの巻数や断面積などの要素によって決まる比例定数です。
変圧器は相互誘導の応用例
相互誘導の応用例として変圧器があります。相互誘導を利用することにより、電圧を変化させるのです。鉄心に一次コイルと二次コイルが存在するとき、以下のように鉄心を曲げることで両端をつなぐと、磁場(磁束)は外に漏れなくなります。
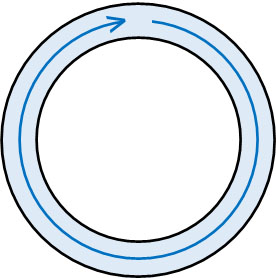
それでは、この鉄心に巻数\(N_1\)の一次コイルと巻数\(N_2\)の二次コイルが存在する場面を考えましょう。下図では、矢印の方向に磁場(磁束)があり、一次コイルの自己誘導起電力を\(V_1\)、二次コイルの相互誘導起電力を\(V_2\)とします。
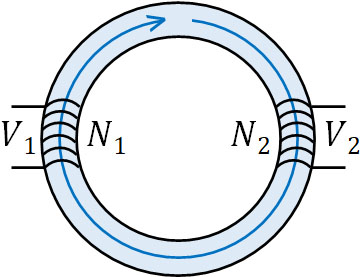
このとき、一次コイルで単位時間当たり(1秒当たり)の磁束変化を\(\displaystyle\frac{ΔΦ}{Δt}\)とすると、ファラデーの電磁誘導の法則より、一次コイルの自己誘導起電力は\(V_1=N_1\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)と表すことができます。
- \(V_1=N_1\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)
磁束の変化に着目するため、\(V_1=L\left|\displaystyle\frac{ΔI}{Δt}\right|\)ではなく、\(V_1=N_1\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)を利用しましょう。
また磁場は漏れないため、二次コイルについても磁束変化は\(\displaystyle\frac{ΔΦ}{Δt}\)です。そのため、二次コイルの相互誘導起電力は\(V_2=N_2\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)です。
- \(V_2=N_2\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)
そこで、自己誘導起電力\(V_1\)と相互誘導起電力\(V_2\)の比を確認しましょう。以下のようになります。
\(V_1:V_2=N_1\left|\displaystyle\frac{ΔΦ}{Δt}\right|:N_2\left|\displaystyle\frac{ΔΦ}{Δt}\right|\)
\(V_1:V_2=N_1:N_2\)
こうして、自己誘導起電力\(V_1\)と相互誘導起電力\(V_2\)の比というのは、コイルの巻数の比によって決まるとわかります。
そのため一次コイルに対して、二次コイルに大きい電圧を生じさせたい場合、二次コイルの巻数を多くすればいいです。一方、二次コイルに小さい電圧を生じさせたい場合、一次コイルに対して二次コイルの巻数を少なくすればいいです。
このようにして、電磁誘導によって発生させる電圧を変えることができるのです。これが変圧器の原理です。
私たちが日常生活で利用する電気は交流です。つまり、常に電流の向きが変わっています。交流では電流が常に変化するため、相互誘導によって新たな電流を起こすのは容易です。そこで変圧器を利用して二次コイルに新たな電流を発生させれば、容易に電圧を変えることができます。
送電で変圧器が利用される理由
参考までに、変圧器は送電などで利用されます。導線にも抵抗があるため、発電所から各家庭に電気を送るとき、抵抗(導線)で発生するジュール熱(消費エネルギー)をできるだけ少なく抑えなければいけません。
ジュールの法則より、ジュール熱を得る公式は\(Q=I^2Rt\)であるため、電流\(I\)の値が小さいほど送電でのロス(ジュール熱の発生)が少ないです。また電流の値を低くするためには、オームの法則より\(V=RI\)であるため、電圧を高くすればいいとわかります。
発電所から送られる電気について、電圧が非常に高いのは、送電でのロスをできるだけ少なくするためなのです。
ただ、非常に高い電圧では一般家庭で利用できません。そこで各家庭に電気を送るとき、変圧器を利用します。コイルの巻数を調節することにより、一般家庭に送るときは電圧を低くするのです。こうして、私たちは日々の生活で電気を利用できるようになります。
自己誘導と相互誘導の原理を学ぶ
電磁誘導が起こるのは、外部による磁場の変化が起こるときだけではありません。コイル自身の環境が変化することによっても電磁誘導が起こります。
コイルに電流が流れると磁場(磁束)が変化します。そのため、磁場の変化を抑えるように電磁誘導が起こります。また他のコイルの影響を受けることによっても電磁誘導が起こります。そこで、自己誘導や相互誘導が起こる原理や公式の導出方法を理解しましょう。
なお、相互誘導の応用例が変圧器です。二次コイルで発生する電圧はコイルの巻数に比例します。そのため、二次コイルで発生させる電圧を自由に調節できます。
電磁誘導は多くの場面で利用されています。その中でも自己誘導と相互誘導は重要な現象であるため、どのような原理になっており、どのように公式を得ればいいのか学びましょう。






