電源には直流電源と交流電源が存在し、電気を学ぶときに私たちが最初に理解しなければいけないのが直流電源です。直流電源によって作られている回路を直流回路といいます。このとき、回路を図示するときは記号を利用します。
また回路を作るとき、抵抗を利用します。抵抗があることにより、流れる電流の量を制限できるのです。
なお抵抗の付け方には、直列接続と並列接続の2種類があります。複数の抵抗を利用するとき、それぞれの抵抗を合計することによって、合成抵抗の値がどのように変化するのか学びましょう。また、回路を書き直すことによってわかりやすくできるようにもなりましょう。
それでは、直流回路での電圧・電流・抵抗の関係はどのようになっているのでしょうか。これらの関係や合成抵抗の計算方法を解説していきます。
もくじ
直流回路の概要と電気用図記号
私たちが日常的に利用しているのは交流電源です。コンセントを利用することによって電気を得る場合、交流電源になります。
一方で電池を利用するなど、電流が一方通行の場合は直流電源となります。電気を学ぶとき、直流回路のほうが理解しやすいです。そのため電流や抵抗を学ぶとき、交流電源より先に直流電源を学ばなければいけません。
なお初めて回路を学ぶとき、電気用図記号を理解できるようになりましょう。何度も利用するため、電気を学んでいる場合は自動的に記号を覚えることになりますが、記号が何を意味しているのか知っておく必要があります。
回路で代表的な記号は以下になります。
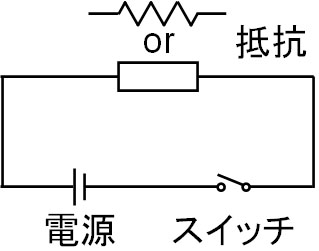
上図のように、抵抗には二種類の表記方法があります。どちらの記号であっても、抵抗であると認識できるようにしましょう。
起電力と電圧(電位差)の考え
なお、電源は正電荷と負電荷が常に一定になるように電荷を移動させます。このときの電圧を起電力といいます。
直流回路でどのように電流が流れるのかについては、水の流れをイメージするとわかりやすいです。電場は正電荷から負電荷へ流れ、電圧\(V\)(電位差)は高低差を表します。電圧が存在することにより、電荷は高い場所から低い場所へと落ちることができるのです。
つまり電池などの電源というのは、ポンプの役割を果たしています。水(電流)を流すためには高低差がなければいけません。そこでポンプ(電源)は水を高い場所へ送り届けます。その後、水はウォータースライダー(抵抗)まで移動し、地面まで滑ります。
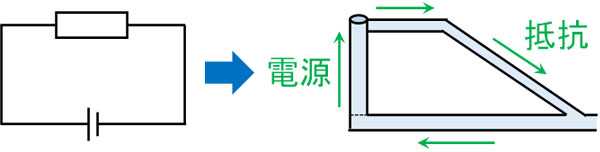
水(電流)が地面まで落ちたら、再びポンプ(電源)によってくみ上げられます。これが繰り返されるのが直流回路です。
なお抵抗によって下落する電圧(電位差)を電圧降下といいます。オームの法則で利用される電圧は電位差を表しており、「抵抗によってどれだけ電圧降下があるのか」を計算できます。高さを加える装置が電源であり、高さを下げる装置が抵抗なのです。
・電圧(電位差)は高さを意味している
そのため電圧というのは、圧力ではなく、高さであると認識しましょう。例えば電池を導線につなぐとき、直列であれば高さは2倍になるため、電流は強くなります。より強力なポンプによって水(電流)を送り出すことができるからです。
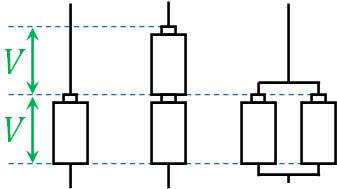
一方で並列に電池を導線へ2つ繋ぐ場合、高さは同じです。そのため電流の勢いは電池一個と電池二個で変化がありません。
複数の抵抗を組み合わせる
なお直流回路を作るとき、複数の抵抗が存在するケースがひんぱんにあります。その場合、どのように抵抗を計算すればいいのでしょうか。
電池などの起電力はあなたが調節できます。それに対して、複数の抵抗を組み合わせる場合、回路全体の抵抗を計算できるようになる必要があります。抵抗の組み合わせ方には以下の二種類があります。
- 抵抗の直列接続
- 抵抗の並列接続
複数の抵抗をまとめ、一つの抵抗とみなす方法を合成抵抗といいます。それぞれのケースについて、合成抵抗を確認していきましょう。
抵抗の直列接続:抵抗を足す
抵抗が存在する場合、そのつどオームの法則を利用する必要があります。例えば抵抗が3つ存在するのであれば、オームの法則を3回利用します。抵抗が100個ある場合、オームの法則を100回利用します。
ただ、抵抗の数だけオームの法則を利用して計算すると面倒です。そこで合成抵抗を利用して、複数の抵抗を一つの抵抗とみなしましょう。例として、以下の回路を比較しましょう。
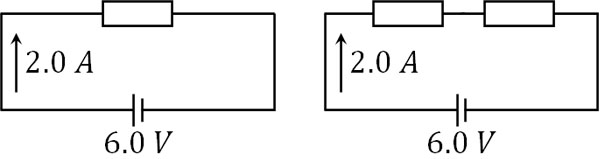
両方とも起電力(電圧)は6.0Vであり、電流は2.0Aです。そのためオームの法則(\(V=RI\))を利用すると、抵抗は3Ωであるとわかります。つまり抵抗が一つの場合であっても、抵抗が二つの場合であっても、上図では条件が同じです。この場合、二つの抵抗を一つの抵抗とみなすことができます。
それでは、合成抵抗を計算してみましょう。以下のように、\(R_1\)と\(R_2\)の二つの抵抗が存在する場面を考えます。
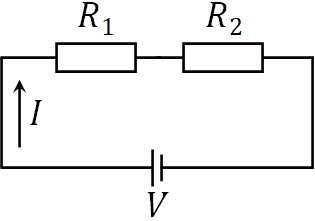
抵抗を直列接続する場合、電圧\(V\)と電流\(I\)は同じです。ただ、二つの抵抗が存在します。電流が抵抗を通るとき、それぞれの電圧降下は\(R_1I\)と\(R_2I\)です。つまり、以下の式を作ることができます。
\(V=R_1I+R_2I\)
\(V=I(R_1+R_2)\)
つまり、合成抵抗\(R\)は以下のようになります。
- \(R=R_1+R_2\)
また、抵抗の数を増やしても考え方は同じであるため、合成抵抗は以下のように計算できます。
- \(R=R_1+R_2+R_3+…\)
直列接続の場合、抵抗を足すことによって合成抵抗を得ることができます。
抵抗の並列接続:逆数を利用して足す
一方で抵抗を並列接続する場合、どのように計算すればいいのでしょうか。前述の通り、電流は水の流れと同じように考えることができます。並列に抵抗をつなぐ場合、水(電流)は二つの道にそれぞれ分かれます。
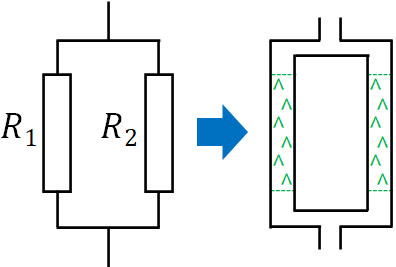
並列でつなぐというのは、必ず枝分かれがあります。枝分かれがあると、その分だけそれぞれの抵抗に流れる電流は弱くなります。一方で電圧降下の大きさ\(V\)は同じです。そのためオームの法則より、それぞれの電流は\(I_1=\displaystyle\frac{V}{R_1}\)と\(I_2=\displaystyle\frac{V}{R_2}\)になります。
なお並列接続での合成抵抗\(R\)を利用する場合、オームの法則より\(V=RI\)です。また、\(I=I_1+I_2\)です。そのため、以下のように式を作りましょう。
\(V=RI\)
\(V=R(I_1+I_2)\)
\(\displaystyle\frac{V}{R}=I_1+I_2\)
\(\displaystyle\frac{V}{R}=\displaystyle\frac{V}{R_1}+\displaystyle\frac{V}{R_2}\)
\(\displaystyle\frac{1}{R}=\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}\)
こうして、\(\displaystyle\frac{1}{R}=\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}\)が成り立つとわかります。また抵抗の数が多くなっても計算方法は同じなので、合成抵抗\(R\)を以下の公式によって計算できます。
- \(\displaystyle\frac{1}{R}=\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+\displaystyle\frac{1}{R_3}+…\)
抵抗の並列接続では、逆数の足し算を利用することによって合成抵抗を計算しましょう。
合成抵抗を利用する練習問題
それでは、合成抵抗を利用することで電圧や電流、抵抗を計算しましょう。以下の問題の答えは何でしょうか。
- 下図のように、起電力\(V\)の電源に抵抗をつないだ直流回路があります。なお、導線の抵抗や電源による内部抵抗は無視できます。
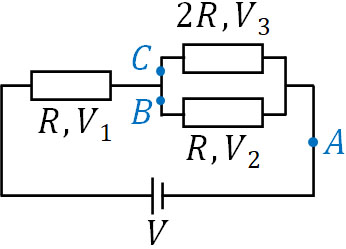
- 点Aでの電流の大きさ\(I_A\)を求めましょう。
- それぞれの抵抗にかかる電圧(\(V_1\)、\(V_2\)、\(V_3\))を求めましょう。
- 点Bと点Cでの電流の大きさ\(I_B\)、\(I_C\)を求めましょう。
1) 点Aでの電流の大きさ\(I_A\)を求めましょう
まず、並列接続での合成抵抗\(R_{23}\)を計算しましょう。以下のようになります。
\(\displaystyle\frac{1}{R_{23}}=\displaystyle\frac{1}{R}+\displaystyle\frac{1}{2R}\)
\(\displaystyle\frac{1}{R_{23}}=\displaystyle\frac{3}{2R}\)
\(R_{23}=\displaystyle\frac{2R}{3}\)
次に、すべての合成抵抗\(R_{123}\)を計算しましょう。
\(R_{123}=R+\displaystyle\frac{2R}{3}\)
\(R_{123}=\displaystyle\frac{5R}{3}\)
つまり、全体では電圧\(V\)、抵抗\(\displaystyle\frac{5R}{3}\)の直流回路とみなすことができます。
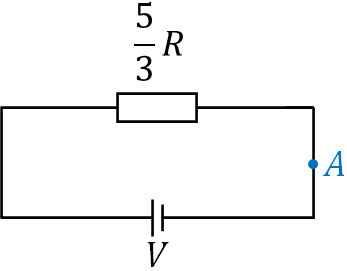
そこでオームの法則より、点Aの電流\(I_A\)を計算しましょう。
\(V=I_A·\displaystyle\frac{5R}{3}\)
\(I_A=\displaystyle\frac{3V}{5R}\)
全体の合成抵抗を利用することにより、\(I_A=\displaystyle\frac{3V}{5R}\)と計算できました。
2) それぞれの抵抗にかかる電圧(\(V_1\)、\(V_2\)、\(V_3\))を求めましょう
\(V_2\)と\(V_3\)では、電圧降下は同じなので\(V_2=V_3\)です。また回路を一周すると、電位差は0になります。そのため、\(V=V_1+V_2\)です(または、\(V=V_1+V_3\))。
そこで、\(V_1\)に着目してオームの法則を利用しましょう。\(V_1\)に流れる電流は\(I_A\)であるため、以下のように計算できます。
\(V_1=RI_A\)
\(V_1=R×\displaystyle\frac{3V}{5R}\)
\(V_1=\displaystyle\frac{3V}{5}\)
また\(V_1=\displaystyle\frac{3V}{5}\)とわかったため、\(V=V_1+V_2\)を利用して\(V_2\)を計算しましょう。
\(V=V_1+V_2\)
\(V=\displaystyle\frac{3V}{5}+V_2\)
\(V_2=\displaystyle\frac{2V}{5}\)
前述の通り、\(V_2=V_3\)です。そのため、\(V_2=V_3=\displaystyle\frac{2V}{5}\)です。こうして、それぞれの抵抗に加わる電圧がわかりました。
3) 点Bと点Cでの電流の大きさ\(I_B\)、\(I_C\)を求めましょう
電圧と抵抗がわかっているため、オームの法則を利用することで電流の大きさを計算できます。
・点Bの電流\(I_B\)
\(\displaystyle\frac{2V}{5}=RI_B\)
\(I_B=\displaystyle\frac{2V}{5R}\)
・点Cの電流\(I_C\)
\(\displaystyle\frac{2V}{5}=2RI_C\)
\(I_C=\displaystyle\frac{V}{5R}\)
こうして\(I_B=\displaystyle\frac{2V}{5R}\)、\(I_C=\displaystyle\frac{V}{5R}\)と計算できました。
回路の書き換えを行う
なお場合によっては、回路の書き直しが必要になるケースがあります。要は、抵抗が直列接続なのか、それとも並列接続なのかわかりにくいのです。
回路の書き換えをする場合、「同じ電位になっているかどうか」に着目しましょう。電源と抵抗を分けて考え、電位の高さが同じになるように図を描くのです。例えば、以下の直流回路はどの部分が直列接続であり、どの部分が並列接続でしょうか。
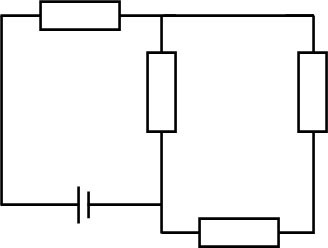
前述の通り、電位差が同じかどうかを確認しましょう。より具体的には、枝分かれしている部分に着目しましょう。枝分かれがある場合、並列接続となるからです。また枝分かれが解消されている場合、並列接続も解消されます。
そこで先ほどの図について、以下のように回路の書き換えをしましょう。
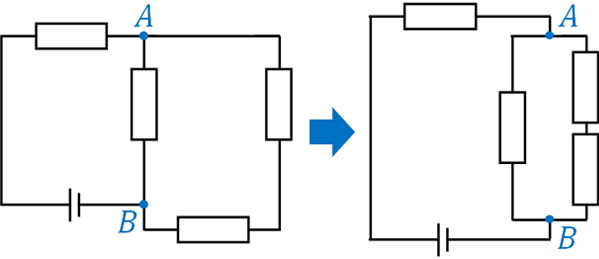
電源につながっている導線は一つであり、枝分かれがある場合、必ずどこかで枝分かれが解消します。そこで上図のように、枝分かれがある場所では抵抗を並列接続し、枝分かれが解消する場所では並列接続を解消させましょう。
直流回路での合成抵抗を計算する
直流電源と交流電源では、直流電源のほうが理解しやすいです。そこで電気を学ぶとき、まずは直流回路の仕組みを理解しましょう。このとき、電圧(電位差)が何を意味しているのか知る必要があります。
なお電圧、電流、抵抗の関係を利用するとき、すべての人がオームの法則を利用します。ただオームの法則を利用するとき、複数の抵抗を一つの抵抗とみなして計算できるようになりましょう。
合成抵抗の計算では、直列接続と並列接続で計算方法が異なります。そこで、直列接続であっても並列接続であっても、合成抵抗を計算してオームの法則を利用できるようになりましょう。このとき、必要に応じて回路の書き直しをするといいです。
電圧、電流、抵抗の関係性を把握しましょう。これにより、オームの法則を利用することで電圧や電流、抵抗の計算を行えるようになります。






