高校数学で学ぶ内容の一つが複素数です。複素数というのは、虚数\(i\)(Imaginary number)を含む数を指します。そのため、複素数も虚数も同じ概念と理解すればいいです。実数と虚数を合わせた数字が複素数です。
虚数を利用して計算するためには、虚数の概念を学ばなければいけません。虚数の公式を覚え、どのように足し算、引き算、かけ算、割り算をすればいいのか理解するのです。
なお、多くの人は「なぜ虚数を学ぶ必要があるのか?」と疑問に思います。そこで、私たちが数学で複素数を学ばなければいけない理由を知りましょう。
それでは、どのように公式を利用して複素数の計算をすればいいのでしょうか。複素数の公式や定義、計算方法を解説していきます。
もくじ
実在しない数字が虚数:二乗すると-1になる数
私たちが平方根を学ぶとき、「平方根の中にある数字は必ず0以上の数になる」と学びました。二乗すると答えは必ず0以上の数になるからです。
そのため\(\sqrt{-a}\)のように、平方根の中にマイナスが含まれることはありません。平方根にマイナスが含まれていると、二乗することによって以下のように答えがマイナスとなり、明らかに矛盾するからです。
- \(\sqrt{-a}^2=-a\)
ただ虚数を学ぶと、平方根の中がマイナスになる数字を利用できるようになります。実際には、平方根の中にある数字がマイナスになることはあり得ません。しかし、そうした空想上の数字が存在すると考え、虚数を利用するのです。
虚数\(i\)は以下のように定義されます。
- \(i=\sqrt{-1}\)
二乗すると-1になる数が虚数です。つまり、\(i^2=-1\)です。このように虚数を利用すれば、二乗によってマイナスとなる数字を得ることができます。例えば、以下のように虚数を利用します。
- \(\sqrt{-4}=4i\)
- \(\sqrt{-b}=bi\)
- \(\sqrt{-\displaystyle\frac{5a+b}{2}}=\sqrt{\displaystyle\frac{5a+b}{2}}i\)
\(i=\sqrt{-1}\)であることを知れば、虚数が何を意味しているのか理解するのは難しくありません。
実数と虚数の違い:複素数の定義
これまで、私たちが学んできた数字は実数です。整数や平方根は実在する値です。一方で実在しない数が虚数です。二乗するとマイナスになる数は存在しないのです。
このとき、実数と虚数の両方を利用して値を表すケースが多いです。実数と虚数を組み合わせた概念が複素数であり、\(a\)、\(b\)を実数とすると、複素数は以下のように定義されます。
- \(a+bi\)
もし\(b=0\)の場合、虚数部分が存在しないため、値は実数です。また\(b≠0\)の場合、数は\(a+bi\)と表すことができ、この数を虚数といいます。なお\(a=0\)の場合、純虚数と呼ばれます。
参考までに、虚数に大小関係はありません。虚数に正の数や負の数は存在しないのです。虚数というのは、あくまでも空想上の数にすぎません。
なぜ虚数を学ぶ必要があるのか
それでは、なぜ私たちは数学で虚数を学ぶ必要があるのでしょうか。実在しない数を利用する意味はないと考える人は多いです。虚数を学ぶ理由は簡単であり、便利だからです。要は、平方根を学ぶ理由と同じです。
平方根を学ぶ前では、多くの人は無理数の概念を理解していません。ただ平方根を利用することによって角度の計算をしたり、三平方の定理を利用したりできるようになります。数学で多くの人が当たり前のように平方根を利用しているのは、平方根が便利だからです。
虚数も同様であり、計算するときに虚数を利用すると便利です。特に大学の物理では、計算過程で虚数が当然のように出てきます。虚数を学んでいないと計算できないものの、虚数を利用することで答えを得られるようになるのです。
物理というのは、複素数を利用しないと機能しません。虚数を利用するからこそ、物理が発展しているのです。
複素数を利用して足し算、引き算を計算する
それでは、複素数を利用して足し算と引き算を行えるようになりましょう。実数と虚数はまったく異なる概念です。そのため、実数部分と虚数部分をわけて足し算または引き算をしましょう。
ルートの足し算をするときであっても、整数とルートをわけて足し算をします。同じように考え、実数と虚数は異なる部分であると捉えなければいけません。
そのため複素数の足し算と引き算では、以下のように計算します。
- \((a+bi)+(c+di)=a+c+(b+d)i\)
- \((a+bi)-(c+di)=a-c+(b-d)i\)
例えば以下のように計算します。
- \((4+2i)+(5+i)=9+3i\)
- \((4+2i)-(5+i)=-1+i\)
実数部分と虚数部分を分けて足し算または引き算をすればいいため、問題なく計算できると思います。
虚数を利用するかけ算
次に複素数のかけ算と割り算を学びましょう。平方根では、整数やルートに関係なくかけ算をすることができます。同じように、虚数についても分配法則を利用してかけ算をしましょう。
- \((a+bi)(c+di)=(ac-bd)\)\(+(ad+bc)i\)
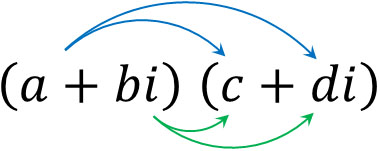
それでは、以下の計算をしてみましょう。
- \((1+2i)(3-4i)\)
分配法則を利用して展開すると以下のようになります。
\((1+2i)(3-4i)\)
\(=3-4i+6i-8i^2\)
\(=11+2i\)
こうして、答えを得ることができました。虚数を含むかけ算では、公式を覚えてもいいし、分配法則を毎回利用してもいいです。
分母の実数化:複素数の割り算
それでは、複素数の割り算はどのように計算すればいいのでしょうか。わり算というのは、分数でもあります。虚数を含む分数(割り算)を計算するとき、分母を実数に変えましょう。利用する公式は以下です。
- \((a+b)(a-b)=a^2-b^2\)
あなたが既に知っているこの公式を利用することで分母を実数にするのです。例題として、以下の分数(複素数の割り算)を計算しましょう。
- \(\displaystyle\frac{1+2i}{2+3i}\)
分母を実数化するため、分子と分母に\((2-3i)\)をかけましょう。
\(\displaystyle\frac{1+2i}{2+3i}\)
\(=\displaystyle\frac{(1+2i)(2-3i)}{(2+3i)(2-3i)}\)
\(=\displaystyle\frac{2-3i+4i-6i^2}{4-9i^2}\)
\(=\displaystyle\frac{8+i}{13}\)
こうして、分母の実数化によって複素数の割り算をすることができました。
複素数の条件と計算問題
ここまで、複素数の計算をする方法を解説してきました。これらの条件を利用して、計算問題を解けるようになりましょう。それでは、以下の問題の答えは何でしょうか。
- 二乗して\(6i\)となる複素数を求めましょう。
複素数の定義は\(a+bi\)であり、\(a\)と\(b\)は実数です。\(a\)と\(b\)が実数であることは重要であり、この前提条件がないと問題を解くことはできません。そこで、以下のように二乗しましょう。
\((a+bi)^2\)
\(=a^2+2abi+b^2i^2\)
\(=(a^2-b^2)+2abi\)
二乗して\(6i\)となる必要があるため、以下の2つの条件を満たさなければいけません。
- \(a^2-b^2=0\)
- \(2ab=6\)
\(a^2=b^2\)であるため、\(a=±b\)です。そこで、\(a=b\)と\(a=-b\)で場合分けをしましょう。
・\(a=b\)の場合
\(2ab=6\)、つまり\(ab=3\)を満たす\(a\)と\(b\)は以下の2通りです。
- \(a=\sqrt{3}\)、\(b=\sqrt{3}\)
- \(a=-\sqrt{3}\)、\(b=-\sqrt{3}\)
そのため、\(\sqrt{3}+\sqrt{3}i\)と\(-\sqrt{3}-\sqrt{3}i\)が答えであるとわかります。
・\(a=-b\)の場合
\(ab=3\)を満たす\(a\)と\(b\)はありません。異なる符号の実数をかけてプラスの答えになることはないのです。そのため、解なしです。
以上の計算結果より、答えは\(\sqrt{3}+\sqrt{3}i\)と\(-\sqrt{3}-\sqrt{3}i\)です。
複素数の概念を知り、虚数を利用できるようにする
多くの人が混乱する内容の一つが虚数です。実在しない数を利用して計算することになり、虚数に大小関係はありません。そのため、なぜ実在しない数を学ぶ必要があるのか理解できないのです。
ただ、虚数は大学で学ぶ科学で必須となる概念です。特に物理では、必ず虚数を利用して計算しなければいけません。虚数があると計算できる範囲が広くなり、非常に便利なのです。
そこで、虚数\(i\)が何を意味しているのか学びましょう。また、複素数の定義を理解しましょう。複素数は実数部分と虚数部分で構成されています。また複素数の足し算、引き算、かけ算、わり算には計算方法があり、四則演算できるようにする必要があります。
新たな概念が虚数であるものの、計算方法は難しくありません。計算に便利なツールとして、虚数\(i\)を利用できるようになりましょう。