複素数を利用して計算するとき、平面を利用するケースがひんぱんにあります。これを複素数平面といいます。
複素数平面では、\(x\)軸を実軸(じつじく)、\(y\)軸を虚軸(きょじく)と考えます。複素数平面は平面ベクトルと考え方が似ており、実軸と虚軸を分けて足し算や引き算を行うことになります。また、三平方の定理を利用することによって距離を得ることができます。
複素数平面が重要なのは、虚数を含む数字について、図示できるようになるからです。複素数平面を利用すれば、実数を利用しての図形と同様に考えることができるのです。
それでは、複素数平面の基本で学ぶべき内容には何があるのでしょうか。また、覚えるべき公式には何があるのでしょうか。複素数平面での足し算や引き算、共役複素数、絶対値、2点間の距離について解説していきます。
もくじ
虚数を利用する複素数平面の性質
私たちが平面上で図形を学ぶとき、通常は\(x\)軸と\(y\)軸を利用します。このとき、\(x\)軸と\(y\)軸の両方とも実数です。
一方で複素数平面では、実数が\(x\)軸に対応し、虚数が\(y\)軸に対応します。例えば\(3+2i\)は以下の点になります。
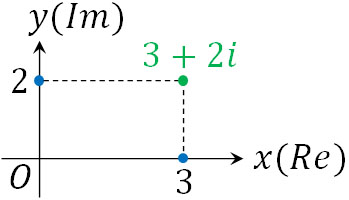
複素数平面を利用しない場合、虚数を含む数字を図示することはできません。一方で複素数平面を利用すれば、虚数を含む数字を図示できます。なお実数と虚数は明確に分ける必要があるため、実軸(\(x\)軸)と虚軸(\(y\)軸)を使い分けましょう。
なお実軸を Re (Real Axis) 、虚軸を Im (Imaginary Axis) と表すことも多いです。
複素数平面での公式:足し算、引き算での平行移動
それでは、足し算をするときは複素数平面でどのような移動になるのでしょうか。複素数では実数と虚数を明確に分けて計算しなければいけません。そこで足し算や引き算をするとき、実軸と虚軸に分けて計算しましょう。
例えば、点A(\(1+2i\))に対して点B(\(3+i\))を加える場合、新たな点は\(4+3i\)となります。
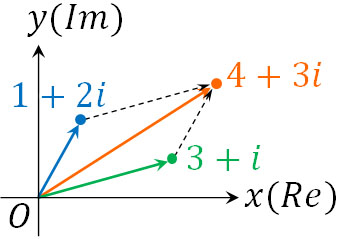
このように足し算や引き算をするとき、点は必ず平行移動します。また平行移動することからわかる通り、複素数平面での足し算と引き算というのは、ベクトルでの足し算・引き算と方法が同じです。
実数と虚数という性質の異なる数を足したり引いたりすることになるため、それぞれの成分を分けて計算しなければいけません。そのため複素数平面での足し算・引き算というのは、ベクトルの足し算・引き算と同じ概念になるのです。
複素数平面とベクトルの関係
なお、複素数平面をベクトルとして捉えることは重要です。ベクトルには虚数が含まれていないため、ベクトルと複素数平面は異なる概念です。ただ、平面での考え方には共通部分が多いのです。
ベクトルには向きと大きさがあります。これは、\(x\)成分と\(y\)成分を別々に考えるからです。複素数平面でも同じように、実軸と虚軸を別々に考えます。そのため複素数平面についても、実軸と虚軸に対して向きと大きさがあると考えることもできるのです。
これが、複素数平面とベクトルで計算方法が多くの場面で共通している理由です。例えば足し算・引き算だけでなく、実数倍する場合についても、ベクトルと複素数平面では計算方法が同じです。ベクトルでは、原点O、点A、点Bが一直線上に存在する場合、以下のように表すことができます(\(k\)は0ではない実数)。
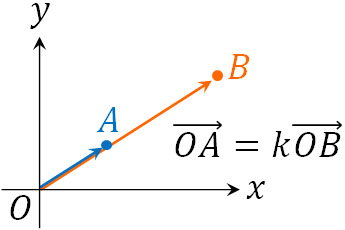
複素数平面についても、同様に実数倍することができます。原点O、点A(\(α\))、点B(\(β\))が一直線上に存在する場合、以下のように表せます。
- \(α=kβ\)
いずれにしても、複素数平面とベクトルは密接な関係にあります。
共役複素数の公式と対称移動
複素数平面を学ぶとき、対称移動も理解しましょう。どのような条件のとき、実軸や虚軸、原点に対して対称となるのか学ぶのです。
このとき、複素数\(z\)に対して共役な複素数を\(\overline{z}\)とします。共役な複素数とは、虚数部分のプラスマイナスが反対になっている複素数を指します。例えば\(1+2i\)に対する共役な複素数は\(1-2i\)です。
そこで、図を描きましょう。共役な複素数では、実軸(\(x\)軸)に対して対称となります。
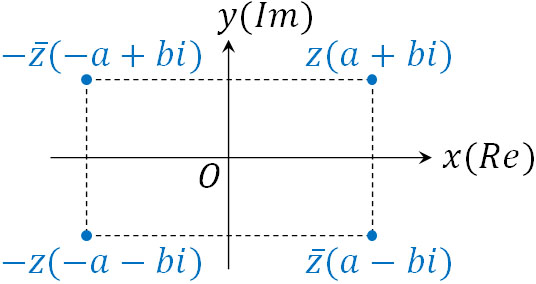
また虚軸(\(y\)軸)に対して対称の場合、\(z\)は\(-\overline{z}\)となります。原点に対して対称の場合、\(z\)は\(-z\)となります。こうした対称移動の中でも、特に重要なのが共役複素数です。
それでは、共役複素数の公式を学びましょう。覚えなくても公式を導出できるものの、共役複素数の関係性を理解することは重要です。
まず、複素数として\(α\)と\(β\)があるとします。\(α\)が実数の場合、以下の関係が成り立ちます。
- \(α=\overline{α}\)
実数の場合、虚数部分が存在しません。そのため虚数部分のプラスマイナスが逆になっても、実数の場合は数字に変化がありません。
一方でαが純虚数の場合、以下の関係が成り立ちます。
- \(α=-\overline{α}\)(\(α≠0\))
純虚数について、共役複素数によってプラスマイナスを反対にした後、マイナスを加えると同じ値になります。
また「虚数部分の符号が反対になった数字」が共役複素数であるため、共役複素数を足すと必ず実数を得ることができます。
- \(α+\overline{α}\)は実数
なお共役複素数には以下の関係もあります。
- \(\overline{α+β}=\overline{α}+\overline{β}\)
- \(\overline{α-β}=\overline{α}-\overline{β}\)
- \(\overline{αβ}=\overline{α}\overline{β}\)
- \(\overline{\left(\displaystyle\frac{α}{β}\right)}=\displaystyle\frac{\overline{α}}{\overline{β}}\)
- \(\overline{\overline{α}}=α\)
これらについては説明しなくても理解できると思います。
複素数の実数条件
それでは、共役複素数の性質を用いて問題を解けるようになりましょう。以下の問題の答えは何でしょうか。
- \(α\overline{β}\)が実数ではないとき、\(α\overline{β}+\overline{α}β\)が実数であることを証明しましょう。
先ほど解説した通り、\(α\)が実数の場合、\(α=\overline{α}\)となります。この性質を利用することによって、実数であることを証明しましょう。
\(z=α\overline{β}+\overline{α}β\)とします。\(α\overline{β}+\overline{α}β\)が実数である場合、\(z=\overline{z}\)となります。そこで、以下の計算をしましょう。
\(\overline{z}=\overline{α\overline{β}+\overline{α}β}\)
\(\overline{z}=\overline{α\overline{β}}+\overline{\overline{α}β}\)
\(\overline{z}=α\overline{β}+\overline{α}β\)
\(\overline{z}=z\)
\(z=\overline{z}\)であるため、\(α\overline{β}+\overline{α}β\)は実数であることを証明できました。
複素数平面での絶対値と2点間の距離
先ほど、複素数平面をベクトルとして考えることができると述べました。そのため絶対値(原点からの距離)や2点間の距離を求めるとき、ベクトルで学んだときの考え方を利用しましょう。
ベクトルで絶対値を加える場合、原点からの距離を意味します。これは複素数平面でも同じです。複素数に対して絶対値を加える場合、それは原点からの距離を意味します。複素数\(α=a+bi\)について、\(|α|=\sqrt{a^2+b^2}\)となります。
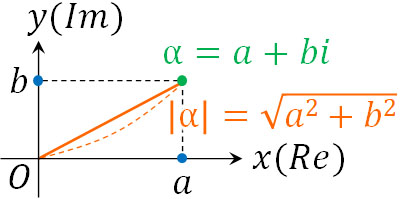
三平方の定理を利用して距離を得るのはベクトルと同様です。
また2点間の距離を計算するときについても、ベクトルと同様に考えて計算しましょう。つまり、実軸と虚軸でそれぞれ引き算をした後、三平方の定理を利用することで計算するのです。点Aを\(α=a+bi\)、点Bを\(β=c+di\)とする場合、2点間の距離(\(|\overrightarrow{AB}|\))は以下のようになります。
- \(|\overrightarrow{AB}|=|β-α|\)
- \(|\overrightarrow{AB}|=\sqrt{(c-a)^2+(d-b)^2}\)
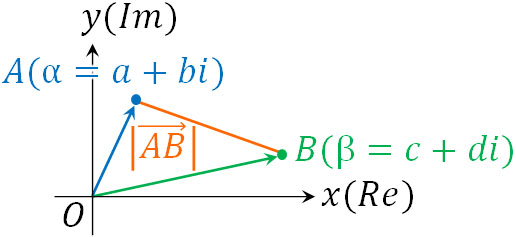
なお絶対値が何を意味しているのか学べば、複素数の絶対値に関する性質を理解できます。まず、複素数\(z\)に対して共役だったり、マイナスが加わったりしても、原点からの距離は同じです。そのため、\(z=a+bi\)とすると以下の関係が成り立ちます。
- \(|z|=|\overline{z}|=|-z|\)
また\(|z|=0\)の場合、\(\sqrt{a^2+b^2}=0\)となります。そのため、以下の関係が成り立ちます。
- \(|z|=0\)の場合、\(z=0\)
なお複素数の計算では、絶対値の二乗を利用するケースがひんぱんにあります。この場合、以下の関係が成り立ちます。
- \(|z|^2=z\overline{z}\)
証明方法は簡単であり、\(z=a+bi\)とすると以下のように計算できます。
\(z\overline{z}=(a+bi)(a-bi)\)
\(=a^2-b^2i^2\)
\(=a^2+b^2\)
\(=|z|^2\)
\(z\)について、原点からの距離は\(\sqrt{a^2+b^2}\)であるため、\(a^2+b^2=|z|^2\)となるのです。ほかにも、絶対値の計算では以下の関係を覚えましょう。
- \(|zw|=|z||w|\)
\(|z|^2=z\overline{z}\)を利用することにより、この関係を証明できます。
\(|zw|^2=zw×\overline{zw}\)
\(=z\overline{z}×w\overline{w}\)
\(=|z|^2×|w|^2\)
\(|zw|>0\)、\(|z|>0\)、\(|w|>0\)であるため、\(|zw|=|z||w|\)です。こうして、公式を証明することができました。なお、この公式はかけ算だけでなく割り算についても成り立ちます。
- \(\left|\displaystyle\frac{z}{w}\right|=\displaystyle\frac{|z|}{|w|}\)
複素数の絶対値が関わる問題では、これらの関係を利用して計算しましょう。以下の問題の答えは何でしょうか。
- \(α=2+i\)のとき、公式\(|z|^2=z\overline{z}\)を利用して、\(|α+2|^2\)の値を計算しましょう。
\(α=2+i\)であるため、\(|α+2|^2\)に代入すると以下のようになります。
\(|α+2|^2=|2+i+2|^2\)
\(=|4+i|^2\)
\(=4^2+1^2\)
\(=17\)
こうして、答えを得ることができます。ただ問題文より、公式\(|z|^2=z\overline{z}\)を利用して計算する必要があるため、\(|α+2|^2\)を変形することで17を導き出しましょう。
\(|α+2|^2\)を変形するとき、\(|α+2|^2=α^2+4α+4\)としてはいけません。左辺は絶対値であるため、答えは必ず実数になります。一方で右辺には\(4α\)が存在し、虚数を含む値になります。そのため、間違いであるとわかります。
そこで、公式を用いて\(|α+2|^2\)を変形しましょう。
- \(|α+2|^2=(α+2)(\overline{α+2})\)
以下のように計算します。
\(|α+2|^2=(α+2)(\overline{α+2})\)
\(=(α+2)(\overline{α}+2)\)
\(=α\overline{α}+2α+2\overline{α}+4\)
\(=|α|^2+2α+2\overline{α}+4\)
\(=5+8+4\)
\(=17\)
\(α=2+i\)であるため、\(|α|^2=5\)です。また\(α\)と\(\overline{α}\)は共役の関係であり、\(2α+2\overline{α}=8\)と実数になります。こうして、答えを得ることができました。
複素数平面の基本と計算方法を学ぶ
虚数を含む場合についても、図形を利用して計算できるようになる必要があります。そのため、複素数平面が重要になります。
複素数平面には、実軸と虚軸という異なる性質の軸が存在します。そのため、ベクトルと同様に考えて足し算や引き算、実数倍をすることができます。原点からの距離や2点間の距離を計算する方法もベクトルと同じです。
ただ、共役な複素数を利用して計算する場合や絶対値の二乗など、複素数に特有の計算方法も存在します。そこで、複素数平面での計算方法を覚えなければいけません。
基本的な計算を行えるのは、複素数平面を理解するうえで必須です。そこで、ここまで解説した内容や公式を覚えましょう。






