円に内接する四角形に特有の定理が存在します。最も有名なのは円周角の定理であり、多くの人が既に理解していると思います。また、四角形では対角を足すことで180°になることも有名です。
これらの性質を利用することによって角度の計算をしたり、証明問題を解いたりできるようになります。複雑な図形について、角度の計算をするのです。
なお、内接する四角形ではトレミーの定理も存在します。有名な定理ではありますが、ほかの定理に比べると重要ではありません。そのため、余力があればトレミーの定理も理解しましょう。
定理を覚えていない場合、定理を利用できないため、問題を解くことはできません。そこで、円に内接する四角形にどのような性質があるのか解説していきます。
必ず覚えるべき円に内接する四角形の定理
円に内接する四角形で必ず覚えるべき定理があります。定理を覚えていない場合、問題を解くことはできません。具体的には、高校数学では以下の定理を必ず覚えましょう。
- 円周角の定理
- 対角の和は180°になる
それぞれの内容を確認していきましょう。
円周角の定理は最も有名
円に内接する四角形では、最も単純な定理の一つが円周角の定理です。三角形を利用する定理ではあるものの、円周角の定理ではほとんどのケースで四角形を含む問題が出されます。そのため、円周角の定理と四角形の関係が重要になります。
円周角の定理では、以下のようにすべての円周角\(a\)は同じになります。
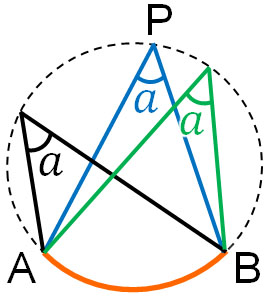
また円周角と中心角を比べるとき、円周角の2倍が中心角の大きさになります。
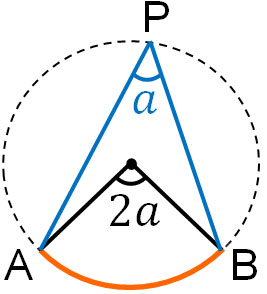
円周角の定理というのは、「円に内接する四角形に関するその他の定理」の基礎となっています。円周角の定理を利用すれば、その他の定理を証明できるのです。
対角の和は180°になる
次に理解するべき内容として、円に内接する四角形では対角の和が必ず180°になります。例えば四角形ABCDについて、∠Aと∠Cを足すと180°になります。また、∠Aは対角の外角と等しくなります。
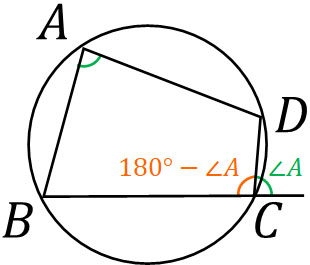
この定理の証明は円周角の定理を利用することで可能です。円の中心をOとすると、∠Aの2倍と∠Cを2倍することで360°になるとわかります。
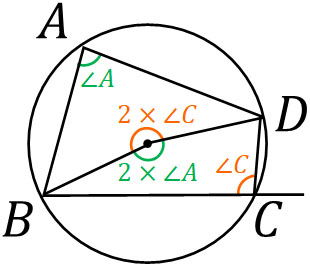
そのため、以下のように定理を証明できます。
\(2×∠A+2×∠C=360°\)
\(∠A+∠C=180°\)
\(∠A=180°-∠C\)
それでは、実際に問題を解いてみましょう。円に内接している以下の四角形について、∠Cを求めましょう。
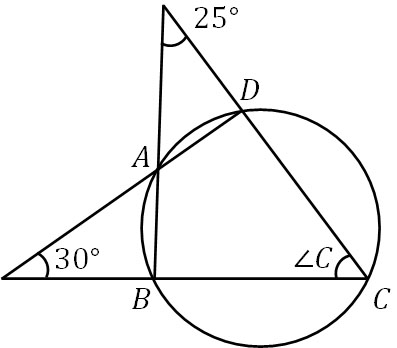
図形の問題を解くとき、わかる角度をランダムに埋めていきましょう。今回の問題では、以下のように角度を記すといいです。
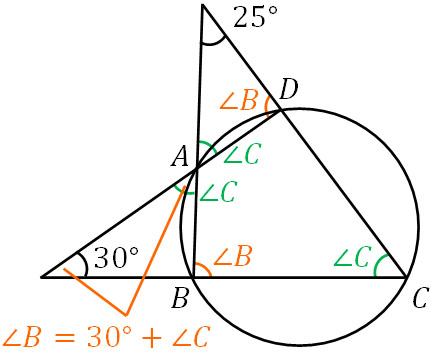
円に内接する四角形では、対角の外角が等しいです。そのため、上図のように∠Cを記入することができます。また、三角形で2つの角度を足すと、残りの角の外角になります。そのため、∠B(∠ABC)は以下のようになります。
\(∠B=30°+∠C\)
また三角形の角度の合計は180°です。そのため、以下の計算によって∠Cを求めることができます。
\(25+∠B+∠C=180\)
\(25+30+∠C+∠C=180\)
\(2∠C=125\)
\(∠C=62.5\)
トレミーの定理も存在する
先ほどの定理に比べて重要度は劣るものの、トレミーの定理も円に内接する四角形で利用できる定理です。トレミーの定理を利用できる場面がある場合、計算時間を大幅に短縮することができます。
トレミーの定理は以下のようになっています。
- 対辺の積+対辺の積=対角線の積
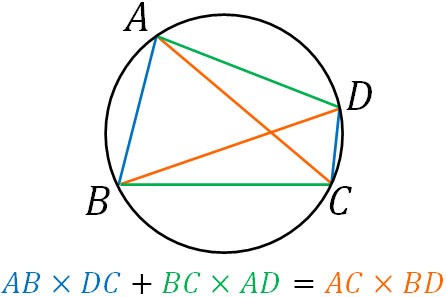
トレミーの定理を利用できる場合、積極的に活用しましょう。図形が円に内接しており、対角線を引くことができるのであれば、トレミーの定理の利用を検討するのです。例えば、以下の問題の答えは何でしょうか。
- 一辺の長さが1である正五角形について、対角線の長さを求めましょう。
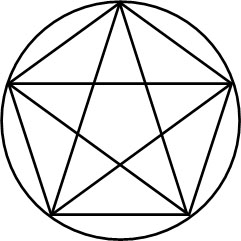
トレミーの定理を利用しない場合、相似図形を用いて問題を解きます。一方、以下のように内接する四角形を想定すれば、トレミーの法則によってすぐに答えを出すことができます。

対角線の長さを\(x\)とすると、トレミーの法則を利用して以下の式を作ることができます。
\(1+x=x^2\)
\(x^2-x-1=0\)
\(x=\displaystyle\frac{1±\sqrt{5}}{2}\)
\(x>0\)なので、\(x=\displaystyle\frac{1+\sqrt{5}}{2}\)と答えを出すことができました。
それでは、なぜトレミーの定理が成り立つのでしょうか。証明方法は複数あり、最もシンプルな方法は余弦定理を用いる方法です。
AB、BC、CD、DAをそれぞれ\(a\)、\(b\)、\(c\)、\(d\)とします。またACを\(e\)、BDを\(f\)とします。このとき、トレミーの法則が成り立つことを証明しましょう。
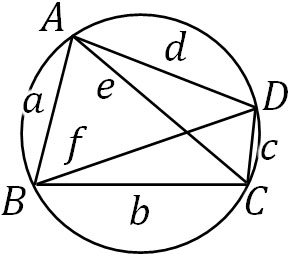
△ABCについて、余弦定理より以下のようになります。
\(cosB=\displaystyle\frac{a^2+b^2-e^2}{2ab}\)
また△ADCについて、余弦定理より以下のようになります。
\(cosD=\displaystyle\frac{c^2+d^2-e^2}{2cd}\)
円に内接する四角形の場合、対角を足すと180°になります。そのため、\(∠D=180°-∠B\)です。そのため、以下のようになります。
\(cosD=\displaystyle\frac{c^2+d^2-e^2}{2cd}\)
\(cos(180°-∠B)=\displaystyle\frac{c^2+d^2-e^2}{2cd}\)
\(cosB=-\displaystyle\frac{c^2+d^2-e^2}{2cd}\)
そのため、以下の式を作れます。
\(\displaystyle\frac{a^2+b^2-e^2}{2ab}=-\displaystyle\frac{c^2+d^2-e^2}{2cd}\)
この等式について、\(e\)について解くと以下のようになります。
\(e^2=\displaystyle\frac{(ac+bd)(ad+bc)}{ab+cd}\)
同様の方法によって、△ABDと△ADCを利用することで\(f\)について解きましょう。
\(f^2=\displaystyle\frac{(ac+bd)(ab+cd)}{ad+bc}\)
そこで、\(e^2×f^2\)を計算しましょう。
\(e^2×f^2\)
\(=\displaystyle\frac{(ac+bd)(ad+bc)}{ab+cd}×\displaystyle\frac{(ac+bd)(ab+cd)}{ad+bc}\)
\(=(ac+bd)^2\)
そこで、平方根を利用して二乗を取り去ると以下のようになります。
\(ef=ac+bd\)
こうして、トレミーの法則を証明することができました。余弦定理を用いる証明方法であっても多少複雑です。ただいずれにしても、この方法によってトレミーの法則を証明することができます。
円に内接する四角形の定理を覚える
四角形の中でも、円に内接する四角形に特有の定理が存在します。そのため円に内接する四角形を発見したら、ここまで解説した定理を利用できないかを考えましょう。
角度を見つけるとき、多くのケースで円周角の定理を利用します。また、対角の和が180°になる性質を利用して角度を計算しなければいけないことも多いです。
それに加えて、重要度は落ちるもののトレミーの定理も理解しましょう。円に内接する四角形について、対角線を引くことができる場合、トレミーの法則を利用できるケースがあります。この場合、辺の長さの計算が楽になります。
なぜこれらの定理が成り立つのかについて、証明を含めて解説してきました。円に内接する四角形が提示された場合、ここまで解説した定理を利用して図形問題を解きましょう。