複素数平面では図形を取り扱うため、内分点や外分点、重心など、これらを図形上で計算できるようになる必要があります。
内分点や外分点、重心は公式が同じであるため、新たに公式を覚える必要はありません。座標やベクトルで内分点、外分点、重心を計算できる場合、複素数平面についても容易に計算することができます。
それでは、複素数平面でどのように公式を利用して計算すればいいのでしょうか。複素数平面で内分点、外分点、重心の問題を解く方法を解説していきます。
複素数平面で内分点の公式は同じ
図形でひんぱんに利用される公式が内分点と外分点です。一般的な図形の問題で利用される内分点・外分点の公式と複素数平面で利用される内分点・外分点の公式は同じです。
点A(複素数\(α\))と点B(複素数\(β\))を\(m:n\)に内分する点C(複素数\(γ\))を得る公式は以下になります。
- \(γ=\displaystyle\frac{nα+mβ}{m+n}\)
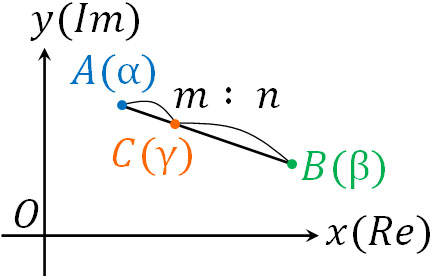
座標、ベクトル、複素数平面とすべてのケースで内分点の公式は同じです。なお、中点は以下の公式によって得ることができます。
- \(γ=\displaystyle\frac{α+β}{2}\)
これらの内容はすでに学んでいるため、容易に理解できると思います。
外分点の公式を利用する
内分点だけでなく、外分点の公式も座標やベクトルと共通しています。複素数平面で外分点を得る公式は以下になります。
- \(γ=\displaystyle\frac{-nα+mβ}{m-n}\)
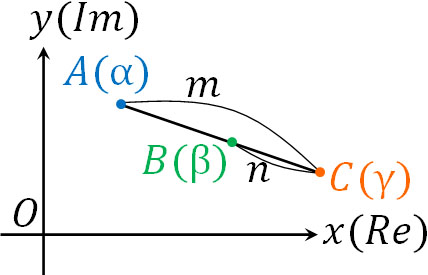
複素数平面で外分点を得るときも、新たに公式を覚える必要はありません。
複素数平面で重心を得る
複素数平面で重心を得る公式もほかのケースと共通です。点A(複素数\(α\))、点B(複素数\(β\))、点C(複素数\(γ\))について、以下が複素数平面で重心G(複素数\(g\))を得る公式です。
- \(g=\displaystyle\frac{α+β+γ}{3}\)
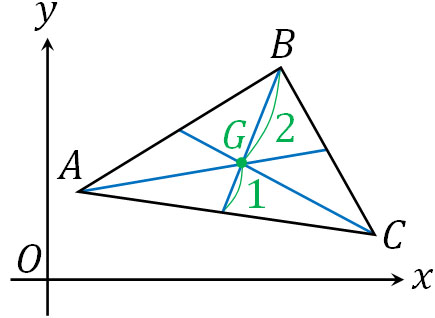
辺の長さが半分となる点(中点)に対して3つの頂点から線を引き、3つの線が交わる点が重心です。頂点と中点を結ぶ線を\(2:1\)に内分する点が重心Gになります。
複素数平面で内分点、外分点、重心を計算する
先ほどの公式を利用することで内分点、外分点、重心を計算してみましょう。複素数では一つの式が\(x\)成分と\(y\)成分を含むため、\(x\)座標と\(y\)座標を別々に計算する必要はありません。それでは以下の問題の答えは何でしょうか。
- A(\(2+i\))、B(\(4+3i\))、C(\(-2+6i\))について、以下の点を表す複素数を求めましょう。
- 線分ABを2:1に内分する点
- 線分ACを3:1に外分する点
- △ABCの重心
1) 線分ABを2:1に内分する点
内分点の公式を利用すると、以下のように内分点を得ることができます。
\(\displaystyle\frac{(2+i)+2(4+3i)}{2+1}\)
\(=\displaystyle\frac{10+7i}{3}\)
2) 線分ACを3:1に外分する点
同様に公式を利用して計算しましょう。
\(\displaystyle\frac{-(2+i)+3(-2+6i)}{3-1}\)
\(=\displaystyle\frac{-8+17i}{2}\)
3) △ABCの重心
公式を利用して、以下のように重心の計算が可能です。
\(\displaystyle\frac{(2+i)+(4+3i)+(-2+6i)}{3}\)
\(=\displaystyle\frac{4+10i}{3}\)
こうして内分点や外分点、重心を計算することができました。
複素数平面で内分点、外分点、重心を得る
座標やベクトルで内分点、外分点、重心の公式を学んでいる場合、複素数平面でこれらの点を得るのは簡単です。座標やベクトルでの計算と同じ公式を利用するからです。
ただ座標やベクトルとは異なり、複素数平面では一つの式が\(x\)成分と\(y\)成分を含みます。この点は座標やベクトルで学ぶ内容と異なるものの、利用する公式や概念は同じなのです。
すでに公式を理解している場合は難しくないため、座標やベクトルと同じ公式を利用して複素数平面での内分点や外分点、重心を計算できるようになりましょう。






