互いに素の関係：最大公約数・最小公倍数と証明問題

小学校で学ぶ約数と倍数の内容が最大公約数と最小公倍数です。この内容について、高校数学でも学びます。当然、高校数学では内容が難しくなります。大きい数字について、どのように最大公約数や最小公倍数を見つければいいのか理解しなければいけません。

また約数と倍数を学ぶとき、「互いに素」となる関係を理解しましょう。互いに素の関係にある数字を利用することによって、最大公約数や最小公倍数の性質を表すことができます。

なお、互いに素の関係を利用することによって証明問題を解かなければいけないことがあります。そこで、互いに素の関係を用いて証明できるようになりましょう。

最大公約数や最小公倍数を学ぶとき、互いに素の関係を理解することが需要です。そこで、互いに素の関係の概念や最大公約数・最小公倍数の性質、証明問題の解き方を解説していきます。

最大公約数の見つけ方：共通する素因数をかける

約数や倍数について、2つ以上の整数を比較するとき、最大公約数と最小公倍数の概念を私たちは既に習っています。

最大公約数や最小公倍数を見つけるとき、どのように計算すればいいのでしょうか。最大公約数については、共通する数字で割れる必要があります。そこで、共通する素数に着目しましょう。例えば、100と360の最大公約数は何でしょうか。以下のように素因数分解をしましょう。

• \(100=2^2×5^2\)
• \(360=2^3×3^2×5\)

そこで、以下の素数に着目します。

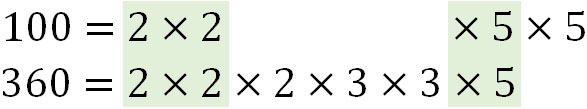
素数を利用してかける場合、当然ながら必ず約数を作れます。このとき共通する素数をすべてかけると最大公約数になります。こうして、100と360の最大公約数は20とわかります。

\(2×2×5=20\)

大きい指数をもつ素因数に着目し、最小公倍数を見つける

一方で最小公倍数はどのように考えればいいのでしょうか。最小公倍数を見つけるとき、すべての素因数について、大きい指数をもつ数字を利用してかけましょう。以下のように考えます。

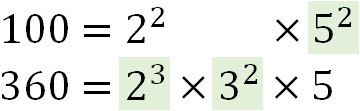
そこで、以下のように計算しましょう。

\(2^3×3^2×5^2=1800\)

こうして、最小公倍数を見つけることができました。素数の中で大きい指数に着目する理由として、公倍数は「互いに足りないものを補うことで発見できる」からです。例えば6と9は以下のよう素因数分解できます。

\(6=2×3\)

\(9=3×3\)

素数で共通しているのは1つの3です。そこで、互いに足りないものを加えましょう。つまり、以下のようにします。

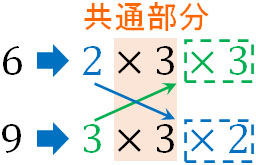
最小公倍数を見つけるために足りない部分を加えるというのは、「大きい指数をもつ素数に着目する」のと意味が同じです。そのため、大きい指数をもつ数字をそれぞれかけることによって最小公倍数を見つけることができます。

互いに素である場合の3つの性質

次に、互いに素の関係を学びましょう。最大公約数と最小公倍数を学ぶことによって、互いに素である自然数を理解できるようになります。互いに素とは、最大公約数が1の関係を指します。例えば、5と8は互いに素です。5と8の最大公約数は1だからです。ほかにも、2と3は互いに素です。

互いに素というのは、要は共通する素因数をもたないことを意味します。このとき、互いに素である場合は3つの性質があります。互いに素である関係に加えて、最大公約数と最小公倍数を利用することによって新たな関係式を作れるのです。

それぞれの性質について確認していきましょう。

最大公約数を利用すると、互いに素の値を得られる

2つの自然数について、公約数を用いて割り算する場合、得られた答えに対して、通常はさらに割り算をすることができます。ただ最大公約数を用いて割り算する場合、それ以上、2つに共通する数字で割ることはできません。言い換えると、最大公約数で割ると互いに素な関係の数字を得ることができます。

例えば、100と360の最大公約数は20です。そのため、以下のように数字を分けることができます。

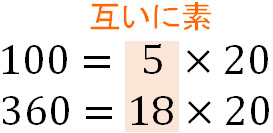
最大公約数で割っているため、必ず互いに素の関係の数字を得られるのは当然です。

そこで、これを数式で表しましょう。自然数\(a\)と\(b\)について、最大公約数を\(g\)とします。この場合、以下の式を作ることができます。

• \(a=a’×g\)
• \(b=b’×g\)

このとき、\(a’\)と\(b’\)は互いに素です。先ほど説明したことを数式で表すと、このような表現になります。

最小公倍数を得るやり方

次に、互いに素の関係を利用して最小公倍数を得ましょう。最大公約数よりも、最小公倍数のほうが値は大きくなります。この理由としては、これまで解説した内容から理解できるはずです。最大公約数では共通する素数をかけて計算するのに対して、最小公倍数は大きい指数をもつ素数を利用してかけ算をします。

このとき、互いに素の数字と最大公約数を利用して、最小公倍数を得ることができます。前述の通り、100と360の最大公約数と最小公倍数は以下のようになります。

• 最大公約数：20
• 最小公倍数：1800

実は最小公倍数というのは、互いに素の数字2つと最大公約数をかけることによって得ることができます。100と360の場合、互いに素の数字は5と18です。そこで、以下のように最小公倍数を計算できます。

\(5×18×20=1800\)

つまり互いに素の数字を\(a’\)と\(b’\)、最大公約数を\(g\)、最小公倍数を\(l\)とすると、以下の数式によって表すことができます。

• \(l=a’×b’×g\)

また、\(a’=5\)と\(b=360\)をかける、または\(a=100\)と\(b’=18\)をかけることによっても最小公倍数となります。

• \(5×360=1800\)
• \(100×18=1800\)

つまり、以下の方法によっても最小公倍数\(l\)を得ることができます。

• \(l=a’×b\)
• \(l=a×b’\)

なお\(l=a’b’g\)を覚えれば、\(l=a’b\)や\(l=ab’\)を覚える必要はありません。前述の通り\(a=a’g\)であり、\(b=b’g\)だからです。

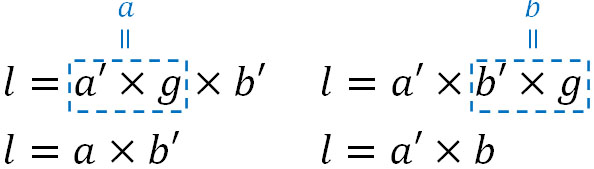
互いに素の関係を学ぶとき、\(l=a’b’g\)を覚える必要があります。一方、\(l=a’b\)や\(l=ab’\)はそのつど作るようにしましょう。

最大公約数と最小公倍数のかけ算を行う

互いの素の関係で3つ目の公式として、最大公約数と最小公倍数のかけ算があります。例として、100と360について考えてみましょう。

前述の通り、この2つの数字の最大公約数は20であり、最小公倍数は1800です。最大公約数と最小公倍数のかけ算の結果というのは、2つの数字（100と360）をかけることによって得ることができます。

\(20×1800=100×360\)

これが互いに素の関係での3つ目の性質です。つまり、以下のように表すことができます。

• \(l×g=a×b\)

なお、この公式についても覚える必要はありません。\(l=a’b’g\)を利用することによって公式を作ることができるからです。\(l=a’b’g\)に対して、両辺に最大公約数\(g\)をかけましょう。

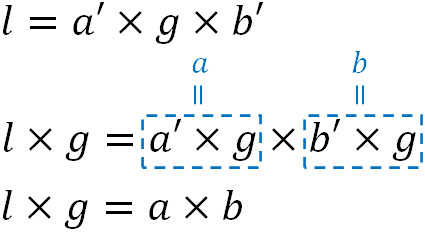
こうして、公式を作ることができます。

最大公約数\(g\)または最小公倍数\(l\)を利用し、数を決定する

互いに素の関係について、最大公約数\(g\)を利用すれば、\(a’\)と\(b’\)（または\(a\)と\(b\)）を得られることは容易に理解できると思います。それに加えて\(l=a’b’g\)を覚えれば、ほかの公式を作ることができます。

それでは、最大公約数や最小公倍数を利用することによって数を決定しましょう。以下の問題の答えは何でしょうか。

• 次の条件を満たす自然数\(a\)と\(b\)をすべて答えましょう。なお、\(a<b\)です。

1. 和が60であり、最大公約数\(g\)が12
2. 積が200であり、最小公倍数\(l\)が40

・問題a

最大公約数\(g\)が12なので、\(a\)と\(b\)を以下のように表すことができます。

• \(a=12a’\)
• \(b=12b’\)

また、和が36なので以下の式を作ることができます。

\(12a’+12b’=60\)

\(a’+b’=5\)

\(a<b\)のとき、\(a’+b’=5\)を満たすケースは以下になります。

\((a’,b’)=(1,4),(2,3)\)

そのため、以下が答えです。

\((a,b)=(12,48),(24,36)\)

・問題b

かけ算を利用するため、\(lg=ab\)を利用することで問題を解きましょう。

\(40g=200\)

\(g=5\)

こうして、最大公約数\(g\)は5とわかりました。また\(l=a’b’g\)なので、以下のようになります。

\(40=5a’b’\)

\(a’b’=8\)

\(a<b\)のとき、\(a’b’=8\)を満たす自然数\(a\)と\(b\)は以下のようになります。

\((a’,b’)=(1,8),(2,4)\)

このうち、\((a’,b’)=(2,4)\)は互いに素ではないので排除しましょう。公約数に2があり、公約数が1だけではありません。つまり、利用するのは\((a’,b’)=(1,8)\)です。

なお、最大公約数\(g\)は5なので自然数\(a\)と\(b\)を以下のように表すことができます。

• \(a=5a’\)
• \(b=5b’\)

そのため、\((a,b)=(5,40)\)が答えです。

互いに素に関する証明問題を解く

なお整数に関する問題ではひんぱんに証明問題が出されます。互いに素に関する内容についても、証明問題を解けるようにしなければいけません。そこで、ここまで解説した内容を理解して証明問題を解きましょう。

互いに素に関する証明問題を解く場合、以下の2つの方法があります。

• 2つの数の最大公約数が\(g=1\)であることを直接証明する
• 背理法を用いて証明する：2つの数が公約数\(p\)をもつと仮定し、矛盾を指摘する

そこで、どちらの方法が最適なのか考えましょう。例えば、以下の問題はどのように証明すればいいでしょうか。

• 連続する2つの自然数が互いに素であることを証明しましょう。

連続する2つの自然数は\(n,n+1\)と表すことができます。\(a\)と\(b\)を互いに素である自然数とすると、以下の式を作ることができます\(a<b\)。

• \(n=ag\)
• \(n+1=bg\)

そこで、\(n=ag\)を\(n+1=bg\)に代入して\(n\)を消去しましょう。

\(n+1=bg\)

\(ag+1=bg\)

\(ag-bg=-1\)

\(g(b-a)=1\)

\(a<b\)なので、\(g>0\)です。つまり\(g=1\)であり、\(b-a=1\)です。\(g=1\)であるため、連続する2つの自然数が互いに素であると証明できました。

背理法を用いて互いに素であることを証明する

それでは、背理法を用いて証明する場合はどのようにすればいいのでしょうか。最大公約数が\(g=1\)であると直接証明できない場合、2つの数が公約数\(p\)をもつと仮定しましょう。その後、矛盾を指摘することによって証明することができます。

自然数\(a,b\)が互いに素であるにも関わらず、\(a=pm\),\(b=pn\)（\(m,n\)は任意の整数）と数式で表すことができる場合、明らかに矛盾しています。

\(a=pm\),\(b=pn\)では、自然数\(a,b\)は両方とも\(p\)の倍数であり、公約数として\(p\)をもちます。これが、自然数\(a,b\)が互いに素であることに対して矛盾しています。そこで、以下の問題について証明しましょう。

• 自然数\(a,b\)が互いに素の場合、\(a+b\)と\(ab\)は互いに素であることを証明しましょう。

自然数\(a,b\)は互いに素であるため、\(a\)と\(b\)が\(p\)の倍数であると矛盾することになります。そこで背理法を利用するため、\(a+b\)と\(ab\)が公約数\(p\)をもつと仮定しましょう。その後、\(a=pm\),\(b=pn\)となることを示します。

ただ、自然数\(a,b\)が\(p\)の倍数である状態というのは、\(a,b\)が互いに素であることと矛盾します。こうして、背理法を用いて証明することができます。そこで、以下のように証明しましょう。

・証明開始

自然数\(a,b\)が共通する公約数\(p\)をもつと仮定すると、以下のように表現することができます。

• \(a+b=pm\)
• \(ab=pn\)

※\(m,n\)は整数

\(ab=pn\)より、\(a\)または\(b\)は\(p\)の倍数です。仮に\(a\)が\(p\)の倍数の場合、以下の数式を作れます。

• \(a=pk\)（\(k\)は整数）

そこで、\(a=pk\)を\(a+b=pm\)に代入しましょう。

\(a+b=pm\)

\(pk+b=pm\)

\(b=pm-pk\)

\(b=p(m-k)\)

\(m-k\)は整数であるため、\(a\)だけでなく\(b\)も\(p\)の倍数です。これは、自然数\(a,b\)が互いに素であることと矛盾します。

なお、仮に\(b\)が\(p\)の倍数である場合についても、\(b\)だけでなく\(a\)も\(p\)の倍数となります。そのため、同様に自然数\(a,b\)が互いに素であることに矛盾します。こうして、背理法を用いて証明することができました。

最大公約数・最小公倍数と互いに素の関係を学ぶ

高校数学で最大公約数・最小公倍数を学ぶ場合、難易度が急に上がります。互いに素の関係を学ぶ必要があり、公式を利用することによって問題を解かなければいけません。

そこで、互いに素の関係のときに利用できる公式を覚えましょう。特に重要なのが以下になります。

• \(a=a’×g\)、\(b=b’×g\)
• \(l=a’×b’×g\)

ほかの公式は最大公約数\(g\)を利用して、そのつど作りましょう。

なお互いに素の関係を利用して証明問題を解かなければいけないことがあります。この場合は最大公約数\(g\)が1であることを直接証明する、または背理法を利用して証明しましょう。こうして、互いに素の関係の問題を解くといいです。