ド・モアブルの定理：1のn乗根と複素数での極形式の関係・公式

複素数平面で学ぶ内容にド・モアブルの定理があります。ド・モアブルの定理を学べば、複素数で\(n\)乗根の計算を行うときに計算が早くなります。また3倍角の導出が可能なので、こうした公式を忘れてしまっても公式を素早く作れるようになります。

ド・モアブルの定理について、公式を覚えてはいけません。そうではなく、なぜ公式が成り立つのか学びましょう。

なおド・モアブルの定理を利用することにより、1の\(n\)乗根の計算も可能になります。この計算についても公式を覚えるのではなく、なぜ公式が成り立つのか理解しなければいけません。

それでは、複素数平面でのド・モアブルの定理はどのような内容なのでしょうか。また、どのように公式を利用して計算すればいいのでしょうか。ド・モアブルの定理と1の\(n\)乗根の計算方法を解説していきます。

1 ド・モアブルの定理の証明と公式
2 1の\(n\)乗根を計算する
- 2.1 図を利用して、1の\(n\)乗根の意味を学ぶ
- 2.2 \(n\)乗根と極形式の関係
3 ド・モアブルの定理を利用して計算する

ド・モアブルの定理の証明と公式

まず、ド・モアブルの定理とは何なのでしょうか。以下が公式になります。

\((cosθ+isinθ)^\color{red}{n}=cos\ \color{red}{nθ}+isin\ \color{red}{nθ}\)

つまり\((cosθ+isinθ)\)を\(n\)乗する場合、\(n\)と角度\(θ\)をかけた式に変えることができます。これがド・モアブルの定理です。

ただ、この公式を覚える必要はありません。複素数平面を学んでいる場合、この公式が成り立つのは当然だからです。\(cosθ+isinθ\)について、複素数を極形式で表すと長さ（絶対値）は1であるため、かけても長さに変化はありません。

一方で\(cosθ+isinθ\)をかけると、偏角\(θ\)の分だけ角度が増えます。そのため\(z=cosθ+isinθ\)の場合、以下のように考えることができます。

\(z^2=cos2θ+isin2θ\)
\(z^3=cos3θ+isin3θ\)
\(z^4=cos4θ+isin4θ\)
…
\(z^n=cos\ nθ+isin\ nθ\)

こうして、ド・モアブルの定理が成り立つと証明できました。より正確に証明したい場合は数学的帰納法を利用しますが、正確に証明をしなくても、公式が成り立つと容易に理解できます。また極形式の性質を理解していれば、ド・モアブルの定理を覚える必要はないとわかります。

複素数の\(n\)乗根の計算を行う

それでは、どのようなときにド・モアブルの定理が有効なのでしょうか。複素数について\(n\)乗根の計算を行うとき、ド・モアブルの定理を利用しましょう。例えば、以下の問題の答えは何でしょうか。

\((1+\sqrt{3}i)^6\)

式の展開によって計算する場合、計算が煩雑です。また二項定理を利用するにしても計算が大変なのは同じです。そこで複素数を極形式で表した後、ド・モアブルの定理を利用して計算しましょう。以下のようになります。

\((1+\sqrt{3}i)^6\)

\(=\left\{2\left(cos\displaystyle\frac{π}{3}+isin\displaystyle\frac{π}{3}\right)\right\}^6\)

\(=2^6\left(cos\displaystyle\frac{6π}{3}+isin\displaystyle\frac{6π}{3}\right)\)

\(=64(cos2π+isin2π)\)

\(=64\)

こうして、答えは64と計算することができました。式に虚数が存在し、さらには\(n\)乗根の計算を行う場合、ド・モアブルの定理を利用することを考えましょう。

複素数を極形式で表し、ド・モアブルの定理を利用する

なおド・モアブルの定理を利用するとき、\(z=cosθ+isinθ\)について、\(z^0=0\)と考えると、\(n=0\)のときも成り立ちます。

また\(n\)が負の整数であってもド・モアブルの定理を利用できます。\(z^{-n}=\displaystyle\frac{1}{z^n}\)であるため、以下のように考えます。

\((cosθ+isinθ)^{-n}\)\(=\displaystyle\frac{1}{(cosθ+isinθ)^{n}}\)\(=\displaystyle\frac{1}{cos\ nθ+isin\ nθ}\)\(=cos(-nθ)+isin(-nθ)\)

この性質を利用することで計算問題を解きましょう。以下の問題の答えは何でしょうか。

複素数\(z\)が\(z+\displaystyle\frac{1}{z}=\sqrt{2}\)となるとき、\(z^{20}+\displaystyle\frac{1}{z^{20}}\)の値を計算しましょう。

まず、複素数\(z\)を求めましょう。両辺に\(z\)をかけて計算すると以下のようになります。

\(z+\displaystyle\frac{1}{z}=\sqrt{2}\)

\(z^2+1=\sqrt{2}z\)

\(z^2-\sqrt{2}z+1=0\)

解の公式より、複素数\(z\)は以下のように計算できます。

\(z=\displaystyle\frac{\sqrt{2}±\sqrt{2}i}{2}\)

そこで、複素数\(z\)を極形式で表しましょう。

\(z=\displaystyle\frac{\sqrt{2}±\sqrt{2}i}{2}\)

\(z=\displaystyle\frac{1}{\sqrt{2}}±\displaystyle\frac{1}{\sqrt{2}}i\)

\(z=cos\displaystyle\frac{π}{4}±isin\displaystyle\frac{π}{4}\)

そこで、ド・モアブルの定理を利用して以下のように計算しましょう。

\(z^{20}+\displaystyle\frac{1}{z^{20}}\)

\(=z^{20}+z^{-20}\)

\(=cos\displaystyle\frac{20π}{4}±i\displaystyle\frac{20π}{4}\)\(+cos\displaystyle\frac{-20π}{4}±i\displaystyle\frac{-20π}{4}\)

\(=cos5π±isin5π\)\(+cos(-5π)±isin(-5π)\)

\(=cosπ±isinπ\)\(+cos(-π)±isin(-π)\)

\(=-2\)

こうして、答えを得ることができました。極形式で表してド・モアブルの定理を利用すれば、たとえ\(n\)の値が大きくても容易に計算できます。

3倍角の公式の導出が可能

ド・モアブルの定理は3倍角の公式を導出するときも有効です。以下が3倍角の公式です。

\(sin3α=3sinα-4sin^3α\)
\(cos3α=-3cosα+4cos^3α\)

加法定理と2倍角の公式を利用することによって3倍角の公式を得ることはできるものの、ド・モアブルの定理を利用すれば、より簡単に3倍角の公式を得ることができます。

ド・モアブルの定理より、以下の式が成り立つのは容易に理解できます。

\((cosθ+isinθ)^3=cos3θ+isin3θ\) – ①

次に、3乗の展開公式を利用することで\((cosθ+isinθ)^3\)を計算しましょう。

\((cosθ+isinθ)^3\)

\(=cos^3θ+3cos^2θ·isinθ-3cosθ·sin^2θ\)\(-isin^3θ\)

\(=cos^3θ-3cosθ·sin^2θ\)\(+i(3cos^2θ·sinθ-sin^3θ)\) – ②

①と②より、以下の関係が成り立ちます。

\(cos3θ+isin3θ\)\(=cos^3θ-3cosθ·sin^2θ\)\(+i(3cos^2θ·sinθ-sin^3θ)\)

実数部分と虚数部分は同じ値になる必要があるため、以下の関係にあるとわかります。

\(cos3θ\)\(=cos^3θ-3cosθ·sin^2θ\) – ③
\(sin3θ\)\(=3cos^2θ·sinθ-sin^3θ\) – ④

次に、\(sin^2θ+cos^2θ=1\)を利用して計算しましょう。

・③へ\(sin^2θ=1-cos^2θ\)を代入する

\(cos3θ\)\(=cos^3θ-3cosθ·sin^2θ\)

\(cos3θ\)\(=cos^3θ-3cosθ(1-cos^2θ)\)

\(cos3θ\)\(=4cos^3θ-3cosθ\)

・④へ\(cos^2θ=1-sin^2θ\)を代入する

\(sin3θ\)\(=3cos^2θ·sinθ-sin^3θ\)

\(sin3θ\)\(=3(1-sin^2θ)·sinθ-sin^3θ\)

\(sin3θ\)\(=3sinθ-4sin^3θ\)

こうして、ド・モアブルの定理を利用することによって3倍角の公式を得ることができました。3倍角の公式を忘れても、このように計算することで公式の導出が可能です。

1の\(n\)乗根を計算する

先ほど、3倍角の公式を得るとき、実数部分と虚数部分を比較しました。この考え方を利用することにより、1の\(n\)乗根を計算できます。言い換えると、\(z^n=1\)の\(z\)を計算するのです。

例として、\(z^6=1\)を解いてみましょう。\(z=±1\)は答えとしてすぐにわかります。それでは、あと4つの解はどのように得ればいいのでしょうか。\(z=r(cosθ+isinθ)\)と考えて計算しましょう。

ド・モアブルの定理より、以下の関係が成り立ちます。

\(z^6=r^6(cosθ+isinθ)^6\)

\(z^6=r^6(cos6θ+isin6θ)\)

次に\(z^6=1\)について、右辺に着目しましょう。1を複素数の極形式で表すと以下のようになります。

\(1=cos0+isin0\)

なお、この式を0°以外の角度でも成り立つように表すと以下のようになります。

\(1=cos2πk+isin2πk\)（\(k\)は整数）

こうして、以下の式を作ることができます。

\(r^6(cos6θ+isin6θ)\)\(=cos2πk+isin2πk\)

この式について、等式を満たす必要があるので\(r=1\)となります。また先ほどと同じように、実数部分と虚数部分を比べましょう。実数部分と虚数部分は同じ値になる必要があります。つまり、以下の関係が成り立ちます。

\(cos6θ=cos2πk\)
\(sin6θ=sin2πk\)

こうして\(6θ=2πk\)であり、\(θ=\displaystyle\frac{π}{3}k\)とわかります。そこで\(0≦θ<2π\)の範囲で計算すると、以下が該当するとわかります。

\(θ=0,\displaystyle\frac{π}{3},\displaystyle\frac{2π}{3},π,\)\(\displaystyle\frac{4π}{3},\)\(\displaystyle\frac{5π}{3}\)

そこで\(z=(cosθ+isinθ)\)に代入すると、以下が答えであるとわかります。

\(z=±1,\)\(\displaystyle\frac{1}{2}±\displaystyle\frac{\sqrt{3}}{2}i,\)\(-\displaystyle\frac{1}{2}±\displaystyle\frac{\sqrt{3}}{2}i\)

こうして、すべての答えを得ることができました。

図を利用して、1の\(n\)乗根の意味を学ぶ

それでは、複素数平面で考えると1の\(n\)乗根は何を意味しているのでしょうか。図を利用すれば、実は計算しなくても一瞬で\(z^6=1\)の答えを得ることができます。

先ほど計算した通り、\(z^6=1\)で角度を計算すると\(6θ=2πk\)になります。つまり\(θ\)は\(2π\)（360°）を6等分しているとわかります。\(k=0\)のとき、\(θ=0\)です。そこで\(θ=0\)を起点として\(2π\)を6等分する場合、以下の図を描けます。

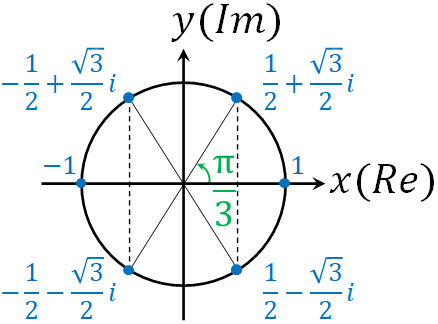
1を極形式で表すと\(1=cos2πk+isin2πk\)となるため、\(z^n=1\)というのは、一つの円を\(n\)等分することを意味しています。そのため図を利用すれば、計算しなくても\(z^6=1\)の答えを得ることができるのです。

複素数平面では、計算によって答えを得られるだけでなく、図形が何を意味しているのか学ぶことも重要です。

\(n\)乗根と極形式の関係

次に、1以外の\(n\)乗根を確認しましょう。基本的な考え方は1の\(n\)乗根と同じであるため、理解するのは難しくありません。以下の問題を解いてみましょう。

\(z^4=8-8\sqrt{3}i\)のとき、\(z\)を求めましょう。

\(z=r(cosθ+isinθ)\)と考えると、\(z^4\)は以下のようになります。

\(z^4=r^4(cos4θ+isin4θ)\)

次に、\(8-8\sqrt{3}i\)を極形式で表しましょう。

\(8-8\sqrt{3}i\)

\(=16\left(\displaystyle\frac{1}{2}-i\displaystyle\frac{\sqrt{3}}{2}\right)\)

\(=16\left(cos\displaystyle\frac{5π}{3}+i\displaystyle\frac{5π}{3}\right)\)

長さ（絶対値）を確認すると、\(r^4=16\)です。\(r>0\)であるため、\(r=2\)です。また実数部分と虚数部分は同じ値になる必要があるため、以下の関係が成り立ちます。

\(cos4θ=cos\displaystyle\frac{5π}{3}\)
\(sin4θ=sin\displaystyle\frac{5π}{3}\)

つまり、偏角は整数\(k\)を用いて以下のように表せます。

\(4θ=\displaystyle\frac{5π}{3}+2πk\)

\(θ=\displaystyle\frac{5π}{12}+\displaystyle\frac{π}{2}k\)

\(0≦θ<2π\)の範囲で考えると、\(k=0,1,2,3\)のときに成り立ちます。そのため\(z=2(cosθ+isinθ)\)へ代入すると、以下の4つの式が答えです。

\(z=2\left(cos\displaystyle\frac{5π}{12}+isin\displaystyle\frac{5π}{12}\right)\)
\(z=2\left(cos\displaystyle\frac{11π}{12}+isin\displaystyle\frac{11π}{12}\right)\)
\(z=2\left(cos\displaystyle\frac{17π}{12}+isin\displaystyle\frac{17π}{12}\right)\)
\(z=2\left(cos\displaystyle\frac{23π}{12}+isin\displaystyle\frac{23π}{12}\right)\)

また、図で表すと以下のようになります。