小学校では整数の割り算を学びます。このとき、わり算をすることによって商と余りを出すことができます。これに対して高校数学では、数式を利用することによって整数の割り算を行い、商と余りを表せるようになりましょう。
数式で表すとなると難しいと感じるかもしれません。ただ割る数と割られる数を利用して、得られる商と余りの関係を把握すれば容易に理解できます。
また整数の割り算を数式で表すことができれば証明問題を解くことができます。整数では証明問題がひんぱんに出されるため、数式を用いて証明できるようになりましょう。
それでは、どのようにして整数の割り算を数式で表し、計算すればいいのでしょうか。ここでは、数式を用いて整数の割り算を行う方法や証明問題の解き方を解説していきます。
もくじ
割り算での商と余りを数式で表す
すべての人が小学校で整数の割り算を学びます。整数の割り算をするとき、以下の4つを利用して計算します。
- 割られる数
- 割る数
- 商
- 余り
例えば、余りを利用するとき、\(42÷8\)の答えは何でしょうか。以下のように記すことができます。
\(42÷8=5\) あまり 2
ただ高校数学で割り算を利用する場面は基本的にありません。そこで、かけ算を利用して\(42÷8\)の商と余りを表しましょう。そうすると、以下のようになります。
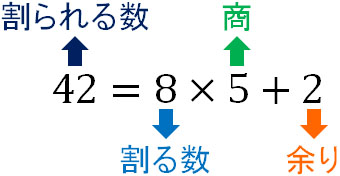
この位置関係を理解すれば、整数の割り算を数式で表すことができます。
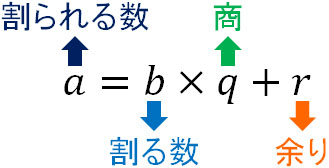
整数の割り算では、必ず\(a=bq+r\)を利用して計算することになります。整数の割り算をする過程を思い出せば、なぜこの数式になるのか理解できます。
数式を利用して余りを求める
それでは、実際に\(a=bq+r\)を利用して計算してみましょう。以下の問題の答えは何でしょうか。
- \(a\)を4で割ると2余り、\(b\)を4で割ると3余ります。\(ab\)の余りは何でしょうか。
\(a\)と\(b\)をそれぞれ数式で表しましょう。以下のようになります。
- \(a=4q+2\)(\(q\)は整数)
- \(b=4q’+3\)(\(q’\)は整数)
そこで\(ab\)を計算すると以下のようになります。
\(ab=(4q+2)(4q’+3)\)
\(ab=16qq’+4(3q+2q’)+6\)
\(ab=4(4qq’+3q+2q’+1)+2\)
こうして、\(ab\)の余りは2であるとわかりました。
余りによって整数を分類する
なお、余りを出すときに重要な考え方があります。それは、余りは割る数よりも小さい値でなければいけないことです。
例えば、42を8で割るときは以下の式を作ります。
\(42=8×5+2\)
一方、以下は間違いです。
\(42=8×4+10\)
式としては成り立つものの、整数の割り算で\(42÷8\)の余りが10になるのは間違いです。そのため、先ほどの例題についても以下のように式を変えました。
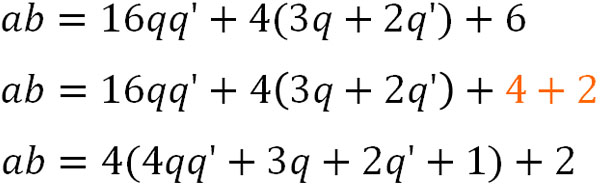
先ほどの例題では、割る数は4です。そのため、余りは4よりも小さくしなければいけません。そのため、このような式に変形しました。
つまり割る数が\(b\)の場合、余りは以下のうちどれかになります。
- \(0, 1, 2, …, b-1\)
次に、余りの数を用いて整数の分類をしましょう。整数として割る数\(m\)が与えられているとき、これを\(k\)倍しましょう。その場合、すべての整数を以下のように表すことができます(\(k\)は整数)。
- \(mk\)、\(mk+1\)、\(mk+2\)、…、\(mk+(m-1)\)
割る数\(m\)を\(k\)倍する場合、余りの数は\(0, 1, 2, …, m-1\)のどれかになります。そのため、すべての整数を表す場合は先ほどの提示したようになります。
割り算を数式で表し、余りを利用して場合分けする
それでは、以下の問題を解いてみましょう。
- 整数\(n\)について、\(n^2\)を4で割ると余りが0または1になることを示しましょう。
4で割るため、以下の4種類の整数\(n\)を想定することができます。
- \(4k\)(\(k\)は整数)
- \(4k+1\)(\(k\)は整数)
- \(4k+2\)(\(k\)は整数)
- \(4k+3\)(\(k\)は整数)
そこで、それぞれについて場合分けをして余りを確認しましょう。
・\(4k\)の場合
\(n^2=16k^2\)であるため、余りは0です。
・\(4k+1\)の場合
\(n^2=(4k+1)^2\)
\(=16k^2+8k+1\)
\(=4(4k^2+2k)+1\)
そのため、余りは1です。
・\(4k+2\)の場合
\(n^2=(4k+2)^2\)
\(=16k^2+16k+4\)
\(=4(4k^2+4k+1)\)
そのため、余りは0です。
・\(4k+3\)の場合
\(n^2=(4k+3)^2\)
\(=16k^2+24k+9\)
\(=4(4k^2+6k+2)+1\)
そのため、余りは1です。
こうして、すべてのケースについて\(n^2\)を4で割ると余りが0または1になることを証明することができました。
整数の式を利用して、倍数が関わる証明問題を解く
先ほど、余りを利用することによって整数の分類を行い、証明問題を解きました。整数を利用する問題では、ここまで解説した整数の式を利用して、倍数が関わる証明問題を解かなければいけないことがあります。
倍数というのは、要は割り算をするのと意味が同じです。整数の式を確認すると、倍数と割る数は同じ位置に存在します。
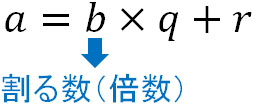
そのため倍数を利用する証明問題については、整数の式を利用して証明しましょう。例えば、以下の問題の答えは何でしょうか。
- 連続する2つの整数の積は2の倍数になることを証明しましょう。
まず、連続する2つの整数は\(n\)と\(n+1\)になります。そのため、2つの整数の積は以下のように表すことができます。
\(n(n+1)\)
それでは、どのようにして「\(n(n+1)\)が2の倍数である」と示せばいいでしょうか。整数が2の倍数というのは、整数を2で割れることを意味しています。そのため、すべての整数を以下のように表すことができます。
- \(2k\)(\(k\)は整数)
- \(2k+1\)(\(k\)は整数)
そこで、先ほどと同じように場合分けすることによって証明しましょう。
・\(2k\)の場合
\(n(n+1)\)
\(=2k(2k+1)\)
・\(2k+1\)の場合
\(n(n+1)\)
\(=(2k+1)(2k+2)\)
\(=2(2k+1)(k+1)\)
いずれの場合も2をかけることになるため、連続する2つの整数の積は必ず2の倍数になります。こうして、証明することができました。
倍数というのは、割る数を利用するのと意味が同じです。そのため倍数の証明問題が出された場合、割り算の数式を利用することによって証明しましょう。
整数について、割り算の式を利用する
私たちは小学校で割り算を学びます。わり算をするとき、商と余りが出ます。高校数学では、これを数式で表します。
数式で表す場合、すべての整数を表現することができます。そこで\(a=bq+r\)の式を利用して計算問題を解きましょう。
また整数の問題では、証明問題がひんぱんに利用されます。証明問題を解くとき、余りを利用して整数を分類しましょう。\(a=bq+r\)を利用して、整数を分類わけした後に証明するのです。なお、倍数を含む整数の証明問題についても解き方は同じです。
高校数学になると、割り算の問題の難易度が非常に高くなります。整数の割り算では数式\(a=bq+r\)を利用することを理解し、計算問題や証明問題を解くようにしましょう。






