接線の傾きを知りたいとき、微分することによって新たな関数を導き出すことができます。微分というのは、接線の傾きを得るための操作です。
微分を学ぶとき、導関数と微分係数を習います。微分係数とは、接線の傾きを指します。また導関数とは、微分することによって得られる新たな関数を指します。微分すると、必ず導関数を得ることができます。
それでは、どのように導関数を出せばいいのでしょうか。また、微分の公式をどのように利用すればいいのでしょうか。
高校数学の微分・積分では、先に微分を習います。微分の初歩は内容が難しくなく、どのように微分すればいいのか解説していきます。
もくじ
傾きを得られる式を作るのが微分
微分とは、何を意味するのでしょうか。数学での微分とは、接線の傾きを得る方法です。
傾きを計算するとき、\(x\)の変化量と\(y\)の変化量を利用して計算します。例えば\(y=x^2\)の関数について、\((1,1)\)と\((3,9)\)を結ぶ直線の傾きはいくらでしょうか。
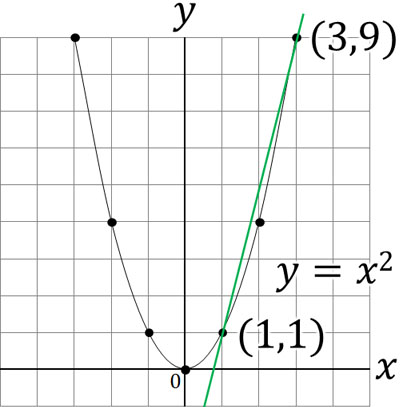
\(x\)が2増えることによって、\(y\)は8増えています。そのため2点を結ぶ直線の傾きは4であるとわかります。
- \(\displaystyle\frac{8}{2}=4\)
微分を理解するとき、「2点の\(x\)の変化量と\(y\)の変化量を確認することで傾きを得られる」ことをまずは理解しましょう。
極限値を利用し、限りなく0に近づけることで微分係数を得る
それでは、文字を利用して傾きを表しましょう。座標Aについて、右にh移動する場合、傾きはどのようになるでしょうか。
例えば座標Aについて、\(x\)座標が\(a\)のとき、\(y\)座標は\(f(a)\)(\(x\)に\(a\)の値を代入した値)です。次に、座標Aから右にh移動した座標Bを考えます。座標Bの\(x\)座標は\(a+h\)です。また点Bの\(y\)座標は\(f(a+h)\)です。そのため、傾きは以下のようになります。
- \(\displaystyle\frac{f(a+h)-f(a)}{(a+h)-a}=\displaystyle\frac{f(a+h)-f(a)}{h}\)

ただ2点を結ぶ場合、それは接線の傾きではありません。接線の傾きを得るには、どのようにすればいいのでしょうか。
先ほど、座標Aから右にh進んだ点を座標Bにしました。それでは、hの距離を0.00000001のように非常に小さい値にすればどうでしょうか。この場合、「2点を結ぶ直線の傾きではあるものの、実質的に一つの点の接線を表している」と考えることができます。
\(h\)の値を0に近づける場合、数学では\(\displaystyle \lim_{ h \to 0 }\)と表現します。そこで以下の式を作ります。
- \(\displaystyle \lim_{ h \to 0 }\displaystyle\frac{f(a+h)-f(a)}{h}\)
この式は「座標A\((a,f(a))\)と座標B\((a+h,f(a+h))\)を結ぶ直線の傾きについて、hの値を極限まで0にする」ことを意味します。
例えば、\(f(x)=x^2\)の関数の場合はどのようになるのでしょうか。座標Aは\((a,a^2)\)となり、座標Bでは\((a+h,(a+h)^2)\)となります。そこで代入すると以下のようになります。
\(\displaystyle \lim_{ h \to 0 }\displaystyle\frac{f(a+h)-f(a)}{h}\)
代入すると、
\(\displaystyle \lim_{ h \to 0 }\displaystyle\frac{(a+h)^2-a^2}{h}\)
\(\displaystyle \lim_{ h \to 0 }\displaystyle\frac{(a^2+2ah+h^2)-a^2}{h}\)
\(\displaystyle \lim_{ h \to 0 }\displaystyle\frac{2ah+h^2}{h}\)
\(\displaystyle \lim_{ h \to 0 }2a+h\)
また\(\displaystyle \lim_{ h \to 0 }\)というのは、\(h≒0\)を意味します。hを無視できるため、以下のようになります。
\(\displaystyle \lim_{ h \to 0 }2a+h=2a\)
こうして\(x\)座標が\(a\)のとき、傾きは\(2a\)になると計算できます。例えば\(x\)座標が3のとき、傾きは6です。また\(x\)座標が4のとき、傾きは8です。こうして、接線の傾きを得ることができます。
このとき得られる接線の傾きを微分係数といいます。例えば\(x=3\)のときの微分係数は6です。\(x=4\)のときの微分係数は8です。
導関数を利用し、接線の傾きを計算する
微分係数を学べば、導関数を理解できます。微分係数も導関数もほぼ同じ概念だからです。先ほど、座標A\((a,f(a))\)での座標を考えました。そこで\(x\)座標を\(a\)ではなく、\(x\)に置き換えてみましょう。
そうすると、\(a\)が\(x\)に置き換わった先ほどと同じ以下の式を作ることができます。
- \(\displaystyle\frac{f(x+h)-f(x)}{(x+h)-x}=\displaystyle\frac{f(x+h)-f(x)}{h}\)

こうして導き出される新たな関数を導関数といいます。
例えば\(f(x)=x^2\)の導関数は\(f'(x)=2x\)です。なお\(f'(x)\)とは、\(f(x)\)を微分した関数を意味します。先ほどと同じように、以下の計算式によって\(f(x)=x^2\)の導関数を導くことができます。
\(f'(x)=\displaystyle \lim_{ h \to 0 }\displaystyle\frac{f(x+h)-f(x)}{h}\)
代入すると、
\(f'(x)=\displaystyle \lim_{ h \to 0 }\displaystyle\frac{(x+h)^2-x^2}{h}\)
\(f'(x)=\displaystyle \lim_{ h \to 0 }\displaystyle\frac{(x^2+2hx+h^2)-x^2}{h}\)
\(f'(x)=\displaystyle \lim_{ h \to 0 }\displaystyle\frac{2hx+h^2}{h}\)
\(f'(x)=\displaystyle \lim_{ h \to 0 }2x+h\)
\(f'(x)=2x\)
こうして得られた新たな関数\(f'(x)=2x\)が導関数です。\(f(x)=x^2\)を微分することによって、\(f'(x)=2x\)を得るのです。
また前述の通り、\(x=3\)のときの微分係数(傾き)は6です。\(x=4\)のときの微分係数(傾き)は8です。微分係数を求めるためには、導関数を得なければいけません。いずれにしても、このようにして接線の傾きを得られます。
導関数の定義を利用して微分する
なお微分するとき、問題によって導関数の定義を利用して微分するように問われるケースがあります。そのため、定義を利用して微分できるようにしましょう。例えば以下の関数について、導関数の定義を利用して微分するとどのようになるでしょうか。
- \(y=x^2-2x\)
導関数の定義を利用すると、以下のようになります。
\(y’=\displaystyle \lim_{ h \to 0 }\displaystyle\frac{(x+h)^2-2(x+h)-(x^2-2x)}{h}\)
\(y’=\displaystyle \lim_{ h \to 0 }\displaystyle\frac{2hx+h^2-2h}{h}\)
\(y’=\displaystyle \lim_{ h \to 0 }2x+h-2\)
\(y’=2x-2\)
こうして、導関数の定義を利用することによって関数を微分することができます。
導関数の公式を利用し、関数を微分する
ただ導関数を求めるとき、定義を利用して微分することはほとんどありません。導関数を求めるための公式を利用して、関数を微分します。
導関数の公式を利用して\(f(x)=x^n\)を微分するとき、以下のようになります。
- \(f'(x)=nx^{n-1}\)
例えば\(f(x)=x^3\)を微分する場合、\(f'(x)=3x^2\)になります。
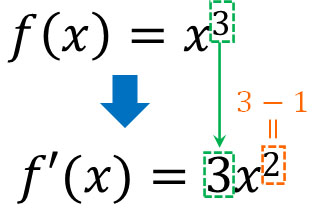
導関数の定義を利用するよりも、導関数の公式を利用するほうが簡単に関数を微分することができます。例えば、以下のようになります。
- \(f(x)=1\)を微分:\(f'(x)=0\)
- \(f(x)=x\)を微分:\(f'(x)=1\)
- \(f(x)=x^2\)を微分:\(f'(x)=2x\)
- \(f(x)=x^3\)を微分:\(f'(x)=3x^2\)
- \(f(x)=x^4\)を微分:\(f'(x)=4x^3\)
微分の公式を利用することで、このように導関数を得ることができます。
導関数の性質を理解し、接線を得られる式を計算する
なお実際に微分するとき、より複雑な関数を微分することになります。そこで導関数の性質を理解しましょう。\(a\)と\(b\)を定数とするとき、導関数には以下の性質があります。
- \(\{a×f(x)\}’=a×f'(x)\)
例えば\(f(x)=3x^2\)を微分する場合、\(f'(x)\)\(=3×2x=6x\)になります。\(f(x)\)\(=-4x^3\)を微分する場合、\(f'(x)\)\(=-4×3x^2\)\(=-12x^2\)になります。
- \(\{f(x)+g(x)\}’=f'(x)+g'(x)\)
例えば\(y=x^3+x^2\)を微分するとき、\(x^3\)と\(x^2\)をそれぞれ微分しましょう。そうすると、導関数は\(y’\)\(=3x^2+2x\)となります。
- \(\{af(x)+bg(x)\}’=af'(x)+bg'(x)\)
例えば\(y=2x^3+3x+2\)を微分するとき、\(2x^3\)と\(3x\)と\(2\)をそれぞれ微分しましょう。そうすると、導関数は\(y’\)\(=6x^2+3\)となります。
これらの性質を利用することによって関数を微分することができます。公式を覚えれば、簡単に導関数を得られます。
導関数を利用して関数を求める
それでは、発展的な問題を解いてみましょう。以下の問題の答えは何でしょうか。
- \(f'(1)=f'(-1)=1\),\(f(1)=0\),\(f(-1)=2\)のとき、この条件を満たす三次関数\(f(x)\)を求めましょう。
\(f(x)\)は三次関数なので、\(f(x)\)\(=ax^3\)\(+bx^2\)\(+cx+d\)と表すことができます。また微分すると以下のようになります。
\(f'(x)=3ax^2+2bx+c\)
そのため、値を代入すると以下のようになります。
\(f'(1)=3a+2b+c=1\)
\(f'(-1)=3a-2b+c=1\)
次に\(f'(1)-f'(-1)\)をすると、\(4b=0\)になります。そのため、\(b=0\)です。\(b=0\)なので、\(f(x)=ax^3+cx+d\)と表せます。
それでは、\(f(1)=0\),\(f(-1)=2\)を代入しましょう。
\(f(1)=a+c+d=0\)
\(f(-1)=-a-c+d=2\)
\(f(1)+f(-1)\)をすると、\(2d=2\)になります。つまり、\(d=1\)です。
また\(f(1)=a+c+1=0\)より、\(c=-a-1\)です。そこで、\(f'(1)=3a+c=1\)に代入しましょう。以下のようになります。
\(3a+(-a-1)=1\)
\(2a=2\)
\(a=1\)
\(a=1\)であるため、\(c=-2\)になるとわかります。そのため、答えは\(f(x)=a^3-2x+1\)です。
微分することによって導関数と微分係数を得る
数学で最も難しいと思われている分野に微分・積分があります。最初に学ぶのが微分であり、ここまでの内容を理解すると、微分の基本的な概念はそこまで難しくないとわかります。
接線を得るために、新たな関数を導き出すのが微分です。微分することによって導関数を得ることができ、導関数がわかれば微分係数(接線の傾き)がわかります。
なお導関数の定義を利用することで微分できるものの、一般的には導関数の公式を利用することによって微分します。そこで導関数の性質を理解して、関数を微分できるようにしましょう。そうすれば、接線の傾きがわかるようになります。
微分は接線の傾きを知るための方法であることを理解し、公式を覚え、導関数を求められるようにしましょう。






