私たちは日常生活でさまざまな計算をします。このとき利用するのが10進法です。0~9が一ケタであり、9よりも数字が大きくなるとケタが一つ上がります。
一方、10進法とは異なる計算方法があります。それがn進法です。nには具体的な数字が入り、2進法や3進法、5進法、16進法などがあります。
高校数学など、高度な数学ではn進法を学びます。これまでの計算方法とは概念が大きく異なるため、n進法の計算は複雑です。ただ時間は12進法や60進法を利用しており、n進法は私たちが身近で利用している概念でもあります。
それでは、n進法とは何なのでしょうか。また、どのように計算すればいいのでしょうか。ここでは、n進法の性質や計算方法、分数・小数との関係を解説していきます。
もくじ
n進法:10進法とは異なるケタの上がり方
n進法とは何かを理解するため、まずは10進法を確認しましょう。n進法というのは、いくつの数字でケタが上がるのかを表します。
例えば10進法の場合、10個の数字を利用した後、一つケタが上がります。0~9には10個の数字が含まれています。そのため9に1が加わると、ケタが一つ上がります。そのため一ケタ、二ケタ、三ケタを確認すると以下のようになります。

10個の数字を集めた後、一つケタが上がるのが10進法です。n進法を理解するためには、最初にこの事実を学ばなければいけません。
2進法、3進法、5進法での数字の表し方
次にn進法の考え方を確認しましょう。まずは5進法の数え方です。前述の通り、n進法はケタが上がる基準を指します。そのため5進法の場合、0~4の数字で成り立ちます。つまり4の次は5ではなく、一つケタが上昇します。
以下が5進法での表記方法です。

5進法で表記する場合、5や6、7などの数字が表れることはありません。必ず0~4の数字を利用して表記することになります。
次に3進法を確認しましょう。3進法の場合、0~2の数字を利用します。3つの数字を利用してケタを表すのが3進法です。

それでは、同じように2進法を利用してケタを表してみましょう。2進法では0と1を利用して表記します。2進法では、2以上の数を利用することはありません。そのため、以下のような表記になります。

n進法を理解するためには、ケタに着目しましょう。n進法では、10進法とは異なる場所でケタが上がります。
なお、n進法は私たちの身近で利用されています。例えばコンピューターでは2進法が利用されています。また秒や分を数えるときは60進法です。60秒や60分というのは、一つ上のケタを意味します。一方、時間は12進法になります。
n進法で表される数字の意味と表記方法
それでは、n進法ではどのように数字を解読すればいいのでしょうか。例えば1402という数字について、10進法と5進法では意味が異なります。
まず、10進法での数字の意味を確認しましょう。前述の通り、10進法では10の数字が集まるとケタが一つ上がります。そのため、1402は以下の数式で表すことができます。
\(2+0×10^1\)\(+4×10^2\)\(+1×10^3\)
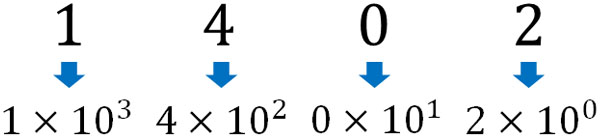
n進法では、この方法と同じやり方で数を表記します。例えば5進法での1402は以下のようになります。
\(2+0×5^1\)\(+4×5^2\)\(+1×5^3\)

それでは、16進法での1402を表すとどのようになるでしょうか。16進法の場合、利用する数字を例えば以下のようにします。
- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
こうして、16の数字と記号を利用します。この場合、16進法での1402は以下のようになります。
\(2+0×16^1\)\(+4×16^2\)\(+1×16^3\)
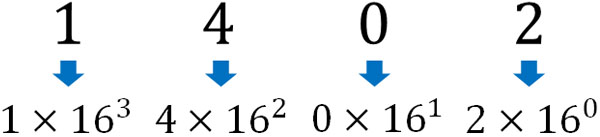
同じ1402ではあっても、何進法なのかによって値が異なります。そこで、10進法ではないケースについても、数字の意味を理解できるようになりましょう。
・n進法の表記方法
なおn進法では表記方法があります。例えば1101について、n進法では以下のように表記します。
- 2進法での1101:1101(2)
- 3進法での1101:1101(3)
- 5進法での1101:1101(5)
- 10進法での1101:1101(10)
- 16進法での1101:1101(16)
このようにカッコ内の数字に着目して、何進法での表記なのか見極めるようにしましょう。
n進法を10進法に直す
それでは、n進法の数字を10進法に直す方法を学びましょう。実際のところ、10進法で記さなければ私たちは数字の大きさを理解できません。そこで、n進法の数字を10進法へと変換するのです。
ここまで解説した内容を理解していれば、n進法を10進法に直す方法は簡単です。累乗の計算をすることによって10進法へ変換しましょう。例えば1402(5)の場合、以下のようになります。
\(2+0×5^1\)\(+4×5^2\)\(+1×5^3=227\)
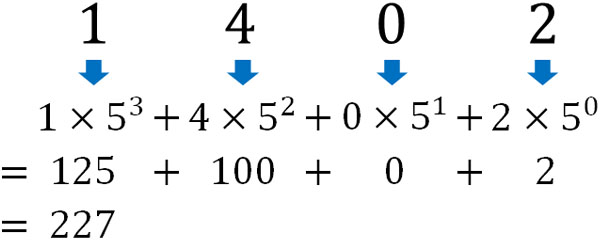
つまり、1402(5)は10進法だと227に該当します。いずれにしてもn進法の数字を10進法に変換するとき、累乗の計算をしましょう。
10進法をn進法に直す
それでは、10進法の数字をn進法に変換する場合はどのようにすればいいのでしょうか。前述の通り、n進法ではn個の数字ごとにケタが上がります。例えば3進法の場合、0~2の数字で表すため、3つの数字を集めたら一つケタが上がります。
そこでn進法では、nで割りましょう。例えば3進法では、3で何度も割ります。また5進法では、5で何度も割ります。
例題として、474を3進法で表してみましょう。この場合、割れなくなるまで3で何度も割ります。その後、最後の商と余りを利用して以下のように3進法へ直します。

一方、5進法の場合は以下のようになります。
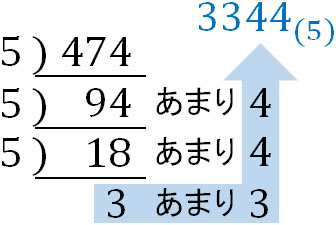
10進法の数字をn進法に変換する方法は共通しています。何度も割り算を行い、商と余りを利用することによってn進法の表記へ変えるようにしましょう。
・n進法をn進法へ直すには、10進法を仲介する
なお場合によっては、n進法の数字をn進法へと変換することがあります。例えば、3進法の数字を5進法へ直すのです。
この場合、10進法を介しましょう。3進法から5進法へ変換したい場合、まずは3進法を10進法にします。その後、10進法を5進法にしましょう。10進法を利用することによって、n進法の数字をn進法へと変換できるようになります。
n進法での四則演算:足し算や引き算、かけ算、割り算を行う
それでは、n進法を利用して四則演算をしてみましょう。10進法での足し算、引き算、かけ算、割り算は既に理解していると思います。それでは、n進法ではどのように計算すればいいのでしょうか。
先に述べた通り、n進法ではケタが重要になります。そこで、ケタに着目して四則演算をしましょう。
・n進法の足し算を行う
繰り上がりの足し算をするとき、10進法では9が基準になります。一方、n進法では繰り上がりの場所に注意して足しましょう。例えば8進法の場合、7の次はケタが一つ上がります。
例題として、8進法で\(25+57\)を計算してみましょう。
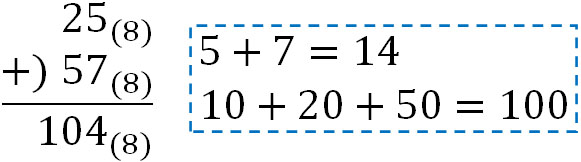
10進法だと\(5+7=12\)です。ただ8進法であるため、7に1を加えると1ケタ上がります。そのため、\(5+7=14\)となります。同様に二桁を計算すると、100となります。こうして、104が答えです。
・n進法の引き算を行う
同様に考えて引き算をしましょう。例えば、5進法で\(42-13\)をする場合は以下の計算になります。
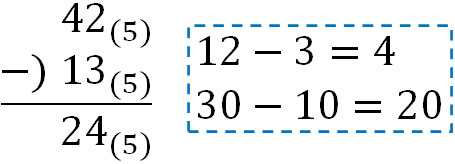
\(2-3\)をすることはできないため、一つ大きいケタから数字を借ります。そこで、\(12-3\)となります。ただ5進法での計算であるため、\(12-3=4\)です。このように、ケタに注意して引き算をしましょう。
・n進法のかけ算を行う
かけ算をするときの注意点は足し算や引き算と同じです。つまり、繰り上がりするときのケタに気をつけましょう。例えば、5進法で\(13×4\)の答えは何でしょうか。計算すると以下のようになります。
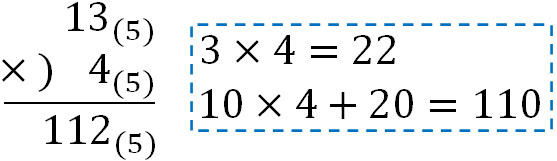
10進法では、\(3×4=12\)です。ただ5進法であるため、12(10)を5進法に直しましょう。そこで12(10)を5進法にすると22(10)になります。同様に5進法で二ケタの計算をすると、最終的にかけ算の答えは112(5)となります。
なおn進法の計算では、10進法に直した後に計算しても問題ありません。先ほどの数字について、10進法に直すと以下のようになります。
- 13(5)は8(10)になる。
- 4(5)は4(10)になる。
\(8×4=32\)であるため、32(10)を5進法に直しましょう。そうすると112(5)になります。
・n進法の割り算を行う
ここまでの解説と同様に、ケタを確認して割り算をしましょう。わり算では引き算とかけ算をするときになるため、ここまで解説した内容を利用して解くことになります。例題として、3進法で\(10011÷12\)を計算してみましょう。
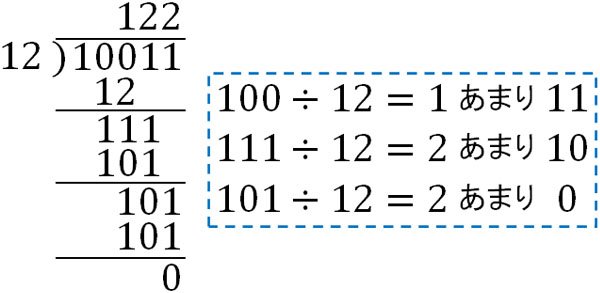
計算が難しい場合、10進法に直して計算しても問題ありません。
- 12(3)は5(10)になる。
- 10011(3)は85(10)になる。
\(85÷5=17\)であるため、17(10)を3進法で表しましょう。そうすると、17(10)を122(3)へ変換できます。
小数・分数とn進法の関係:n進法を10進法に変換する
それではn進法で表現するとき、分数や小数との関係はどのようになるのでしょうか。まず、10進法での分数と小数を理解しましょう。
ケタが大きくなる場合、10進法では10の累乗を利用します。一方、分数や小数の場合、10進法では\(\displaystyle\frac{1}{10}\)ずつケタが小さくなります。例えば0.1402の場合、以下のように表現します。
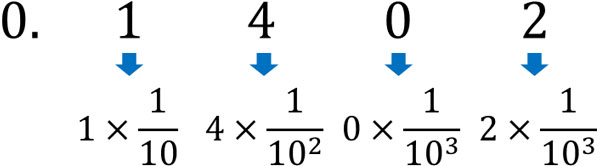
そのため、例えば0.1402(2)は以下のようになります。
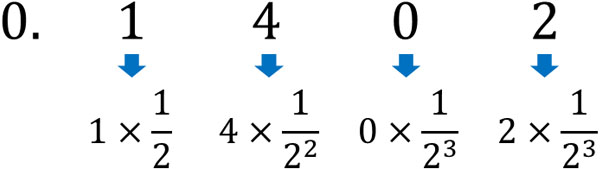
2進法では0と1を利用して数を表現するため、このような意味になるのです。
それでは、0.102(3)を10進法で表すとどのようになるでしょうか。2進法であっても3進法であっても、考え方は同じです。そこで、以下の計算をしましょう。
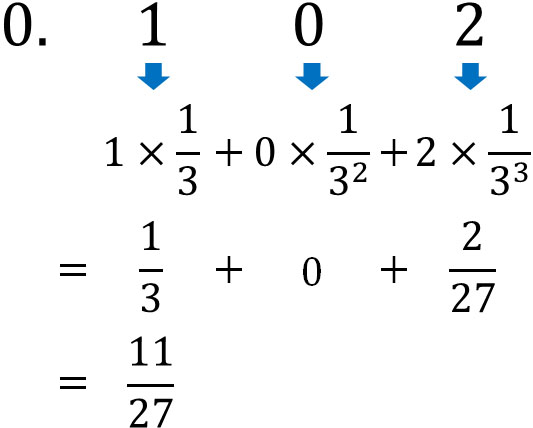
こうして、n進法の小数を分数(10進法)に直すことができます。
小数を利用し、10進法をn進法へ変換する
次に、10進法での分数(または小数)をn進法に変換できるようにしましょう。10進法の整数をn進法へと変換するとき、数字nを利用し、割り切れなくなるまで何度も割り算をすると解説しました。
そこで、これと反対のことをしましょう。つまり、nを利用して小数部分に対して何度もかけ算をします。その後、得られた答えの整数部分を順に並べることによってn進法へ変換することができます。例えば2進法の場合、小数部分へ何度も2をかけます。3進法の場合、小数部分へ何度も3をかけます。その後、整数部分を確認しましょう。
・2進法へ変換する
例題として、0.25(10)を2進法と3進法の小数で表しましょう。2進法への変換では、以下のように計算します。
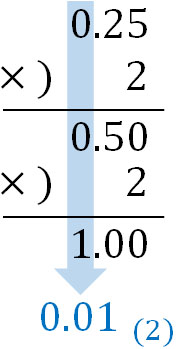
0.25(10)を2進法へ直す場合、最終的に小数部分が0になります。0に対しては何をかけても答えが0であるため、小数部分が0になる場合は計算を止めましょう。
・3進法へ変換する
次に、0.25(10)を3進法で表しましょう。
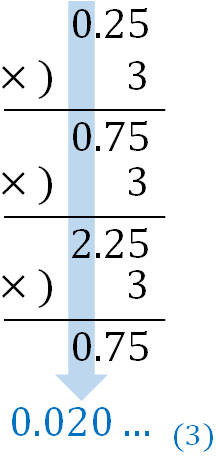
前述の通り、整数部分は無視して、少数部分のみをかけます。かけ算をするとき、小数部分では25と75が繰り返されます。そのため、0.25(10)を3進法で表すと0.0202020…となります。
分数をn進法の小数へ変換する
次に、分数(10進法)をn進法の小数へ変換しましょう。やり方は先ほどと同じであり、整数部分と小数部分(分数部分)を分けます。
例えば0.25というのは、要は\(\displaystyle\frac{1}{4}\)です。そこで\(\displaystyle\frac{1}{4}\)を小数にするとき、2をかけることによって整数部分と小数部分を分けましょう。
・2進法へ変換する
\(\displaystyle\frac{1}{4}\)を2進法の小数にするとき、以下のように計算します。
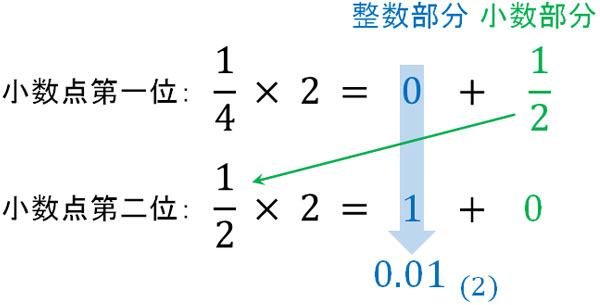
していることは先ほどと同じです。2をかけた後、整数と小数(分数)に分けましょう。その後、小数(分数)の部分のみ取り出し、再び2をかけます。その後、整数の部分だけ取り出して順に並べましょう。
・3進法へ変換する
同様に、\(\displaystyle\frac{1}{4}\)を3進法の小数に直しましょう。

3をかけた後、整数部分と分数部分を分けます。これを繰り返し、整数部分を集めると0.0202020…になります。こうして、3進法の小数へと変換することができました。
n進法の概念や計算方法を理解する
私たちが数学を学ぶとき、10進法を利用してきました。そのためn進法は新たな概念であり、計算方法が違うので混乱しやすいです。
そこで、n進法の概念を理解しましょう。ケタに着目するのがn進法であり、n個の数字を集めるとケタが一つ上がります。そのため足し算や引き算、かけ算、割り算をするときの計算ミスに注意しましょう。
また、小数や分数との関係性も重要です。1より小さい数についてもn進法で表すことができるようになりましょう。
n進法はコンピューターサイエンスで特に活躍します。IT技術者を目指す人にとってn進法を学ぶのは必須であるため、n進法を利用して計算できるようになりましょう。