直線は図形で最も利用されます。直線を利用することによって平行や垂直、角度を作ることができます。三角形も直線によって作られます。
複素数平面で直線を利用することは多く、複素数平面での直線の方程式を学びましょう。複素数平面で利用される直線の方程式は複数あります。そこで平行条件や垂直条件を理解しましょう。また、垂直二等分線を表す方程式も重要です。
これらの方程式を利用できるようになれば、三角形の形状を判断できたり、円の接線の方程式を得たりできるようになります。
複素数平面と直線の方程式について、なす角や平行、垂直、垂直二等分線、三角形を利用してどのように計算すればいいのか解説していきます。
もくじ
複素数平面での2直線によるなす角
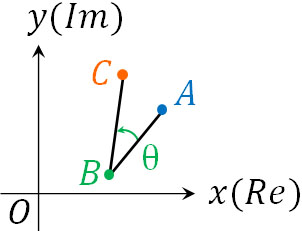
複素数平面で直線の計算をするとき、2直線によるなす角を計算できるようになりましょう。例えば∠ABCを得るとき、どのように計算すればいいでしょうか。
複素数平面で極形式を学んでいる場合、点B(\(β\))を中心として点A(\(α\))を\(θ\)だけ回転し、\(r\)だけ拡大させるとき、回転後の点C(\(γ\))を得る計算方法をすでに知っていると思います。以下の式を作れます。
- \(γ=r(α-β)(cosθ-isinθ)+β\)
なぜ、この式を得られるのかわからない場合、複素数の極形式を復習しましょう。それでは、この式を以下のように変形します。
\(γ=r(α-β)(cosθ-isinθ)+β\)
\(γ-β=r(α-β)(cosθ-isinθ)\)
\(\displaystyle\frac{γ-β}{α-β}=r(cosθ-isinθ)\)
\(\displaystyle\frac{γ-β}{α-β}\)を計算することで式を\(r(cosθ-isinθ)\)へ変形すれば、偏角\(θ\)を得られるとわかります。また偏角\(θ\)が∠ABCであり、2直線によって作られるなす角を表します。
なお、複素数平面はベクトルと関連付けることも可能です。そのように考えると、\(\displaystyle\frac{γ-β}{α-β}\)は\(\displaystyle\frac{BC}{BA}\)です。
ちなみに、角度を計算するときは\(\displaystyle\frac{γ-β}{α-β}=\displaystyle\frac{BC}{BA}\)ではなく、\(\displaystyle\frac{α-β}{γ-β}=\displaystyle\frac{BA}{BC}\)を利用しても問題ありません。2直線のなす角は変わらないため、どちらであっても同じ答えになります。
例えば以下の図について、∠BACはいくらでしょうか。
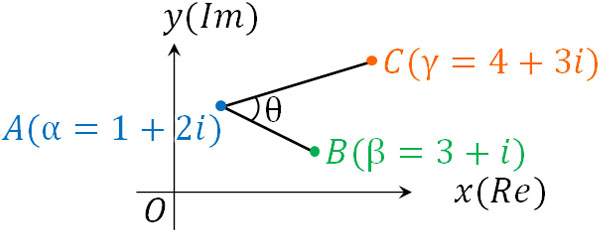
点Aを起点に考えればいいため、\(\displaystyle\frac{\color{red}{A}C}{\color{red}{A}B}=\displaystyle\frac{γ-α}{β-α}\)を計算しましょう。
\(\displaystyle\frac{γ-α}{β-α}\)
\(=\displaystyle\frac{4+3i-(1+2i)}{3+i-(1+2i)}\)
\(=\displaystyle\frac{3+i}{2-i}\)
\(=\displaystyle\frac{(3+i)(2+i)}{(2-i)(2+i)}\)
\(=\displaystyle\frac{5+5i}{5}\)
\(=1+i\)
\(=\sqrt{2}\left(\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{2}}i\right)\)
こうして、∠BACは45°とわかります。また、\(\displaystyle\frac{AC}{AB}\)の比が\(\sqrt{2}\)であることもわかります。
3つの点が同一線上に存在するケース
先ほど解説した内容を理解すれば、3つの点が同一線上に存在するケースがわかります。同じ線の上に点が存在する場合、2つの点を結ぶと偏角は0または\(π\)になります。
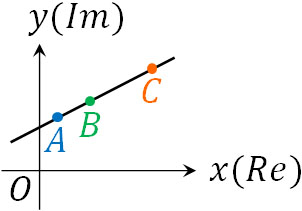
偏角が0または\(π\)であるため、\(\displaystyle\frac{γ-β}{α-β}\)\(=r(cosθ-isinθ)\)に\(θ=0,π\)を代入すると、必ず実数を得られます。つまり、\(\displaystyle\frac{γ-β}{α-β}\)が実数になる場合、3つの点は同一線上に存在するとわかります。
2直線のなす角をどのように得るのかを学び、角度の性質を利用すれば、複素数平面で3点が同じ直線上に存在するケースがわかるのです。
平行条件と垂直条件:解が純虚数、実数になるパターン
次に平行条件と垂直条件を学びましょう。点A(\(α\))、点B(\(β\))、点C(\(γ\))、点D(\(δ\))について、ABとCDが平行な場合を考えてみましょう。なす角を計算するとき、以下の式を作ります。
- \(\displaystyle\frac{AB}{CD}=\displaystyle\frac{β-α}{δ-γ}\)
このとき、平行であれば偏角は必ず0または\(π\)になります。そのため平行の場合、\(\displaystyle\frac{β-α}{δ-γ}\)を計算すると必ず実数になります。
一方でABとCDが垂直な場合、偏角は必ず\(\displaystyle\frac{π}{2}\)または\(\displaystyle\frac{3π}{2}\)になります。
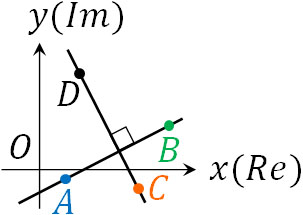
\(r(cosθ-isinθ)\)について、\(θ\)が\(\displaystyle\frac{π}{2}\)または\(\displaystyle\frac{3π}{2}\)の場合、純虚数になります。そのため\(\displaystyle\frac{β-α}{δ-γ}\)を計算して純虚数を得られる場合、ABとCDは垂直です。
円の接線の方程式を導出する
それではここまで解説した内容を利用して、複素数平面での円の接線の方程式を計算しましょう。以下の問題の答えは何でしょうか。
- 原点Oを中心とする半径\(r\)の円があります。点P(\(z\))から円上の点A(\(α\))に対して接線を引くとき、\(\overline{α}z+α\overline{z}=2r^2\)が成り立つと証明しましょう。
\(\overline{α}z+α\overline{z}=2r^2\)が複素数平面での円の接線の方程式です。そこで、この方程式を証明しましょう。まず、以下の図を作ります。
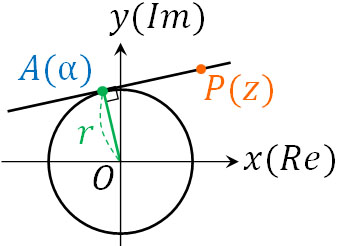
点Pが接線上に存在する場合、\(OA⊥AP\)であるため、\(\displaystyle\frac{AP}{OA}=\displaystyle\frac{z-α}{α-0}\)は純虚数になります。また点Pが点Aに存在する場合、\(z=α\)となるため、\(\displaystyle\frac{AP}{OA}=\displaystyle\frac{z-α}{α-0}\)\(=0\)です。
そのため、以下の関係が成り立ちます。
- \(\displaystyle\frac{z-α}{α}=-\overline{\left(\displaystyle\frac{z-α}{α}\right)}\)
純虚数の場合、共役複素数に対してマイナスを加えると同じ値になります。そこで、以下のように計算しましょう。
\(\displaystyle\frac{z-α}{α}=-\overline{\left(\displaystyle\frac{z-α}{α}\right)}\)
\(\displaystyle\frac{z-α}{α}=-\displaystyle\frac{\overline{z}-\overline{α}}{\overline{α}}\)
\(\displaystyle\frac{z-α}{α}+\displaystyle\frac{\overline{z}-\overline{α}}{\overline{α}}=0\)
\(\overline{α}(z-α)+α(\overline{z}-\overline{α})=0\)
\(\overline{α}z+α\overline{z}-2α\overline{α}=0\)
\(\overline{α}z+α\overline{z}=2α\overline{α}\)
\(\overline{α}z+α\overline{z}=2|α|^2\)
なお点A(\(α\))に対して、原点からの距離(絶対値)は\(r\)です。つまり\(|α|=r\)であるため、以下の式が成り立ちます。
- \(\overline{α}z+α\overline{z}=2r^2\)
こうして、円の接線の方程式を導出できました。この方程式を覚える必要はなく、図の性質を利用して方程式を証明できるようになりましょう。
2点を結ぶ垂直二等分線の公式と図形
複素数平面で直線の方程式を学ぶとき、垂直二等分線の公式も理解しましょう。点A(複素数\(α\))と点B(複素数\(β\))に対して、距離が同じである点P(複素数\(z\))は以下の公式で得られます。
- \(|z-α|=|z-β|\)
絶対値を利用することにより、複素数平面での長さを表すことができます。そのため、この公式が成り立つのは容易に理解できると思います。また点Pは点Aと点Bからの距離が等しければいいです。そこでいくつもの点Pをつなげると直線になり、この直線が垂直二等分線です。
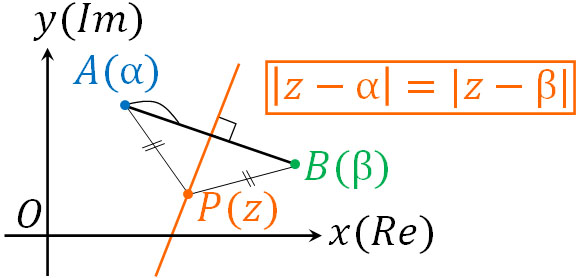
それでは、複素数平面での垂直二等分線の方程式を用いて練習問題を解きましょう。以下の問題の答えは何でしょうか。
- \(|2z-3|=|2z-i|\)を満たす点\(z\)はどのような図形でしょうか。
以下のように式を変形しましょう。
\(|2z-3|=|2z-i|\)
\(|z-\displaystyle\frac{3}{2}|=|z-\displaystyle\frac{1}{2}i|\)
式を確認すると、点\(z\)は\(\displaystyle\frac{3}{2}\)と\(\displaystyle\frac{1}{2}i\)からの距離が等しい点とわかります。言い換えると、\(\displaystyle\frac{3}{2}\)と\(\displaystyle\frac{1}{2}i\)を結ぶ線分の垂直二等分線です。

式を確認することにより、どのような性質の図形なのか判断できるようになりましょう。
複素数平面での三角形の形状
ここまで解説した知識を利用して、複素数平面での三角形の形状を把握できるようになりましょう。三角形の形状を確認するためには、2つの直線による角度(偏角)を得る必要があります。そこで点A(\(α\))、点B(\(β\))、点C(\(γ\))について、以下の式を作ります。
- \(\displaystyle\frac{γ-α}{β-α}=a+bi\)
また、\(a+bi\)を極形式で表しましょう。
- \(\displaystyle\frac{γ-α}{β-α}=r(cosθ+isinθ)\)
これにより、∠BACの偏角\(θ\)を得ることができます。また以下の関係が成り立つため、辺の比を得ることができます。
- \(\left|\displaystyle\frac{γ-α}{β-α}\right|=\displaystyle\frac{AC}{AB}=r\)
こうして、三角形の形状を求めます。それでは、以下の問題の答えは何でしょうか。
- 複素数平面で原点O、点A(\(α\))、点B(\(β\))について、\(α^2-2αβ+4β^2=0\)と\(|α-β|=4\)を満たすとき、△OABの面積を計算しましょう。
\(β≠0\)であるため、\(α^2-2αβ+4β^2=0\)の両辺を\(β^2\)で割りましょう。
\(α^2-2αβ+4β^2=0\)
\(\left(\displaystyle\frac{α}{β}\right)^2-2\displaystyle\frac{α}{β}+4=0\)
解の公式を利用すると、\(\displaystyle\frac{α}{β}\)の答えは以下のようになります。
\(\displaystyle\frac{α}{β}=1±\sqrt{3}i\)
\(\displaystyle\frac{α}{β}=2\left(\displaystyle\frac{1}{2}±\displaystyle\frac{\sqrt{3}}{2}i\right)\)
\(\displaystyle\frac{α}{β}=2\left\{cos\left(±\displaystyle\frac{π}{3}\right)+isin\left(±\displaystyle\frac{π}{3}\right)\right\}\)
\(\displaystyle\frac{α}{β}=\displaystyle\frac{α-0}{β-0}\)\(=\displaystyle\frac{OA}{OB}\)です。そのため、∠AOBの角度は\(\displaystyle\frac{π}{3}\)です。また\(\displaystyle\frac{OA}{OB}=2\)であるため、\(OA:OB=2:1\)です。
∠AOBの角度が\(\displaystyle\frac{π}{3}\)であり、\(OA:OB=2:1\)の場合、△OABは直角三角形であることを意味します。なお偏角は\(±\displaystyle\frac{π}{3}\)であるため、以下の2パターンが存在します。
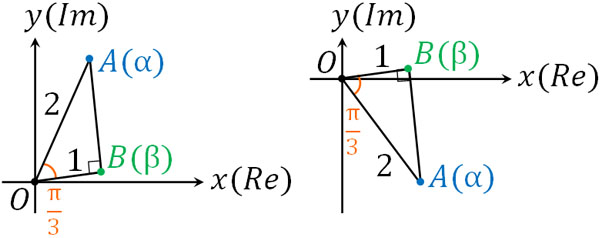
面積は同じであるため、どちらか一方を利用して面積を計算しましょう。なお\(|α-β|=4\)であるため、以下の関係が成り立ちます。
- \(|α-β|=BA=4\)
つまり、ABの長さは4です。△ABCは直角三角形であるため、OBの長さは\(\displaystyle\frac{4}{\sqrt{3}}\)です。そこで、以下のように面積を計算しましょう。
\(\displaystyle\frac{1}{2}×4×\displaystyle\frac{4}{\sqrt{3}}=\displaystyle\frac{8}{\sqrt{3}}\)
\(=\displaystyle\frac{8\sqrt{3}}{3}\)
こうして、△OABの面積を得ることができました。
三角形の重心を表す複素数
次に、複素数平面を利用して証明問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 原点Oを中心とする半径1の円上に点A(\(α\))、点B(\(β\))、点C(\(γ\))があります。この円上に存在しない点H(\(z\))が\(z=α+β+γ\)を満たすとき、点Hは△ABCの垂心であることを証明しましょう。
垂心というのは、三角形の頂点から辺に対して垂直に引いた線の交点を指します。そのため、以下の図を作れます。

点Hが△ABCの垂心であることを証明するためには、以下の2つを示せばいいです。
- \(AH⊥BC\)
- \(BH⊥AC\)
\(AH⊥BC\)であることを示すため、\(\displaystyle\frac{AH}{BC}=\displaystyle\frac{z-α}{γ-β}\)が純虚数であることを示しましょう。純虚数であれば、共役複素数にマイナスを加えることで値が等しくなります。\(\displaystyle\frac{z-α}{γ-β}\)に対する共役複素数は\(\overline{\left(\displaystyle\frac{z-α}{γ-β}\right)}\)であるため、以下の式を作って計算しましょう。
\(-\overline{\left(\displaystyle\frac{z-α}{γ-β}\right)}\)
\(=-\displaystyle\frac{\overline{z}-\overline{α}}{\overline{γ}-\overline{β}}\)
\(=-\displaystyle\frac{\overline{α+β+γ}-\overline{α}}{\overline{γ}-\overline{β}}\)
\(=-\displaystyle\frac{\overline{β}+\overline{γ}}{\overline{γ}-\overline{β}}\)
なお点A(\(α\))、点B(\(β\))、点C(\(γ\))は原点Oを中心とする半径1の円上に存在するため、以下の関係が成り立ちます。
\(|α|=|β|=|γ|=1\)
\(|α|^2=|β|^2=|γ|^2=1\)
\(α\overline{α}=β\overline{β}=γ\overline{γ}=1\)
\(α≠0\)、\(β≠0\)、\(γ≠0\)でるため、\(\overline{α}=\displaystyle\frac{1}{α}\)、\(\overline{β}=\displaystyle\frac{1}{β}\)、\(\overline{γ}=\displaystyle\frac{1}{γ}\)が成り立ちます。そこで、先ほど計算した共役複素数に代入しましょう。
\(-\displaystyle\frac{\overline{β}+\overline{γ}}{\overline{γ}-\overline{β}}\)
\(=-\displaystyle\frac{\displaystyle\frac{1}{β}+\displaystyle\frac{1}{γ}}{\displaystyle\frac{1}{γ}-\displaystyle\frac{1}{β}}\)
\(=-\displaystyle\frac{γ+β}{β-γ}\)
\(=\displaystyle\frac{γ+β}{γ-β}\)
\(=\displaystyle\frac{(α+γ+β)-α}{γ-β}\)
\(=\displaystyle\frac{z-α}{γ-β}\)
こうして、\(\displaystyle\frac{z-α}{γ-β}=-\overline{\left(\displaystyle\frac{z-α}{γ-β}\right)}\)とわかりました。共役複素数にマイナスを加えることで等しくなったため、\(\displaystyle\frac{z-α}{γ-β}\)は純虚数です。言い換えると、\(AH⊥BC\)です。
同様に計算をすると、\(BH⊥AC\)となります(計算過程は省きます)。こうして\(AH⊥BC\)と\(BH⊥AC\)がわかったため、点Hは△ABCの垂心です。
線の方程式を利用し、複素数平面での図形の問題を解く
線は図形で最も利用されます。そのため、複素数平面で線の方程式を計算するのは重要です。複素数平面では点の回転を表現できます。そこで、2つの直線によって作られるなす角を計算できるようになりましょう。
2直線のなす角を計算できれば、平行条件と垂直条件を理解できます。平行の場合、偏角は0または\(π\)です。また垂直の場合、偏角は\(\displaystyle\frac{π}{2}\)または\(\displaystyle\frac{3π}{2}\)です。この性質を利用することにより、複素数平面での図形の問題を解けるようになります。
また複素数平面では垂直二等分線の方程式を利用したり、三角形の形状を計算したりできます。そこで方程式や極形式を利用して、どのような図形なのか判断できるようになりましょう。
複素数平面で直線の方程式を利用すれば、平行や垂直に加えて、三角形の性質を計算できるようになります。これらの性質を学び、複素数平面で図形の計算を行えるようになりましょう。






